USING HARD AND SOFT VITERBY ALGORITHM IN PROGRAM FOR TEXT MESSAGE DECODING

Чернецова Е.А.¹, Шишкин А.Д.²

¹ORCID: 0000–0001–5805–3111, Кандидат технических наук, доцент,

²ORCID:0000–0003–1992–5663, Кандидат технических наук, доцент,

^1,2Российский Государственный Гидрометеорологический Университет

ИСПОЛЬЗОВАНИЕ ЖЕСТКОГО И МЯГКОГО АЛГОРИТМА ВИТЕРБИ В ПРОГРАММЕ ДЛЯ ДЕКОДИРОВАНИЯ ТЕКСТОВОГО СООБЩЕНИЯ

Аннотация

Представлена программная модель декодирования текстового сообщения, полученного по каналу с аддитивным гауссовским шумом. Для передачи сигнала используется многопозиционная фазовая манипуляция, число позиций может быть задано пользователем. Для защиты от ошибок используется сверточный код, параметры которого могут быть заданы пользователем. При декодировании используется мягкий и жесткий алгоритм Витерби. Наглядность представления выходных данных – исходного текстового сообщения и декодированных сообщений – позволяет использовать данную программу в учебном процессе при изучении темы сверточного кодирования.

Ключевые слова: программная модель, кодер, декодер, алгоритм, многофазная манипуляция.

Chernetsova E.A.¹, Shishkin A.D.²

¹ORCID: 0000-0001-5805-3111, PhD in Engineering, Associate professor,

²ORCID: 0000-0003-1992-5663, PhD in Engineering, Associate professor,

^1,2Russian State Hydrometeorological University

USING HARD AND SOFT VITERBY ALGORITHM IN PROGRAM FOR TEXT MESSAGE DECODING

Abstract

A software model for decoding a text message received via a channel with additive Gaussian noise is presented. A multi-position phase shift keying is used for signal transmission; the number of positions can be set by the user. To protect against errors, a convolutional code is used, the parameters of which can be set by the user. Soft and hard Viterbi algorithm is used at decoding. The obviousness of the output data, the source text message, and decoded messages allows using this program in the learning process when studying the subject of convolutional coding.

Keywords: software model, encoder, decoder, algorithm, multiphase keying.

При изучении принципов построения телекоммуникационных систем в рамках дисциплины «Системы и сети передачи информации» [1] , студенты часто испытывают трудности с пониманием алгоритма работы мягкого и жесткого декодирования Витерби. Поэтому была поставлена цель создать программную модель, которая могла бы наглядно продемонстрировать обучающимся разницу в приеме информации, передаваемой по каналу с аддитивным белым гауссовским шумом в незакодированном и закодированном виде, и продемонстрировать результат декодирования текстового сообщения с использованием жесткого и мягкого алгоритма Витерби. Широкое распространение алгоритма Витерби заключается в том, что сложность декодера Витерби не является функцией количества символов в последовательности кодовых слов [2].

В программной реализации используется многофазная манипуляция. Данный вид модуляции был выбран потому, что он может быть использован в каналах связи, имеющих достаточно ограниченный частотны ресурс, но к которым предъявляются высокие требования по качеству передачи информации [3]. Согласно [4], к основным показателям, характеризующим тот или иной модуляционный формат, следует отнести помехоустойчивость и спектральную эффективность, под которой понимают полосу частот, необходимую для передачи сигналов с требуемой скоростью и достоверностью.

В общем случае, данные показатели тесно взаимосвязаны между собой. Это приводит к тому, что улучшение одного из них невозможно без снижения качества другого. Между тем, переход на цифровые системы передачи информации во многом предопределил типы используемых модуляционных форматов, к которым, в первую очередь, следует отнести различные виды манипуляций, как наиболее полно соответствующих дискретной природе передаваемой битовой информации.

Однако, возможности широко известных форматов манипуляции фактически исчерпаны, а их дальнейшая модернизация не позволяет получить существенного выигрыша. В связи с этим, в последнее время наметилась тенденция на переход к формированию сигналов в базисах, отличных от гармонических [5], [6]. В частности, вейвлет–базисы, базисы сплайн–характеров и др. Однако такой подход предполагает полную замену приемо–передающего оборудования, что сложно осуществить в существующих реалиях. Между тем, по мнению зарубежных специалистов [7], [8], традиционные виды модуляции еще до конца не исчерпали свои возможности. Повышению скорости передачи информации в канале способствует увеличение позиционности модуляционного формата, однако при этом возрастает битовая ошибка. В настоящее время компромиссным решением для систем передачи информации по радиоканалу является использование модуляционных форматов на основе ФМн–2 и ФМн–4 [7].  В разработанной программе число позиций модуляции можно задавать.

Модели систем, представленные в пакете Матлаб Simulink для реализации жесткого и мягкого декодирования по алгоритму Витерби [9] разработаны для исходных данных, представляющих собой поток битов.

Модель декодера Витерби для детектирования двоичного фазоманипулированного сигнала, представленная в [10], также разработана для исходных данных, представляющих собой поток битов, и реализует только алгоритм жесткого декодирования Витерби .

По сравнению с рассмотренными моделями систем, реализующими жесткое и мягкое декодирование по алгоритму Витерби [9], [10], разработанная программа в пакете Матлаб предназначена для исходных данных, представленных в виде текстового сообщения, и позволяет студентам ознакомиться с программным кодом, реализующим все преобразования сообщения от текстового вида до сигнала в фазовой или квадратурной фазовой манипуляции. Студенты также получают представление о формировании алгоритма кода Грея, когда двоичные символы отличаются только одной битовой позицией. В этом случае при появлении ошибки в М–арном символе высока вероятность того, что ошибочным является только один из k прибывших битов [11]. Несмотря на то, что в версиях Матлаб, появившихся после 2006 года, предусмотрена реализация алгоритма кода Грея в виде одной команды, предлагаемая программа позволяет студентам не только посмотреть график получившегося сигнального созвездия, но и реализовать алгоритм кода Грея «пошагово», тем самым закрепив их знания об алгоритме его формирования.

Для реализации декодирования Витерби в программной модели используетсятот факт, что данный алгоритм используется в двоичном входном канале с жестким или мягким 3–х битовым квантованным выходом. Длина кодового ограничения варьируется от 3 до 9, причем степень кодирования кода редко оказывается меньше 1/3, и память путей составляет несколько длин кодового ограничения. [12]. В алгоритме декодирования Витерби все пути по решетке кода пошагово сравниваются с принятой из канала связи кодовой последовательностью и отбрасываются те из них, которые точно будут находиться на большем расстоянии, чем другие. Таким образом, главным недостатком данного алгоритма становится необходимость анализа всех путей, выходящих из рассматриваемого узла кодовой решетки. Этот недостаток легко преодолевается благодаря большим вычислительным возможностям современных компьютеров. А благодаря тому, что сложность декодера Витерби не является функцией количества символов в последовательности кодовых слов , он находит широкое применение в современных цифровых системах связи. Алгоритм декодирования Витерби также хорошо использовать в тех случаях, когда шум в канале связи стационарен и легко моделируется.

В жесткой схеме декодирования по алгоритму Витерби используется расстояние Хэмминга, определяемое как количество элементов, которыми различаются два кодовых слова.

Основное различие между мягким и жестким декодированием по алгоритму Витерби состоит в том, что в мягкой схеме не используется метрика расстояния Хэмминга, поскольку она имеет ограниченное разрешение. Метрикой расстояний, которая имеет нужное разрешение, в данном случае выступает евклидово кодовое расстояние, поэтому, чтобы облегчить ее применение в программной модели соответствующим образом преобразуются двоичные числа из единиц и нулей в восьмеричные числа от 0 до 7. Выигрыш в значении битового отношения сигнал/шум при использовании «мягкого» решения составляет EbNo≈ 2 дБ ( рис.1) [13].

Алгоритм программы состоит из следующей последовательности действий:

1. Ввод текстовой строки сообщения.
2. Преобразование текста в ASCII –код.
3. Преобразование символов ASCII –кода в бинарные символы.
4. Формирование из бинарных символов последовательности бит для подачи на вход кодера.
5. Кодирование бинарной последовательности кодом Грея
6. Кодирование бинарной последовательности сверточным кодом для защиты от ошибок
7. Применение фазовой манипуляции к закодированной и незакодированной последовательности битов. Возможность выбора параметров манипуляции.
8. Моделирование прохождения закодированной и незакодированной последовательности битов через канал с гауссовым шумом. Возможность выбора отношения сигнал/шум в канале связи.
9. Демодуляция закодированной и некодированной последовательности бит
10. Декодирование закодированной последовательности бит с использованием жесткого и мягкого алгоритма Витерби.
11. Расчет квадрата евклидова расстояния между исходным текстовым сообщением и принятыми сообщениями: не подвергавшимся кодированию; декодированному по жесткому алгоритму Витерби и декодированному по мягкому алгоритму Витерби. Определение ассимптотической эффективности кодирования.

Результат работы программной модели при значении битового отношения сигнал/шум EbNo=4,5 дБ представлен на рисунке 2. Как можно видеть, сообщение , декодированное с помощью «мягкого» алгоритма полностью совпадает с исходным, тогда как в принятом некодированном сообщении и в сообщении, декодированном с помощью «жесткой» схемы, есть ошибки.

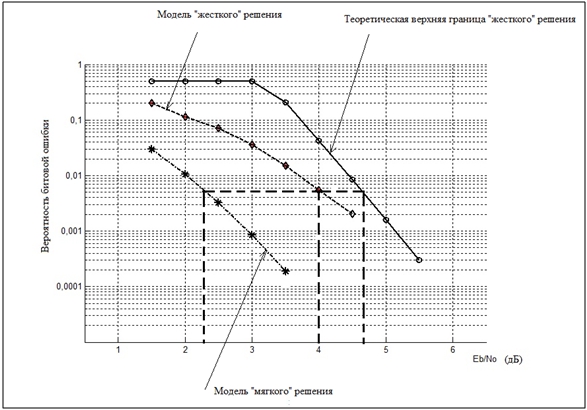
Риc. 1 – Графики зависимости вероятности битовой ошибки от битового отношения сигнал/шум

 

Асимптотическая эффективность кодирования в программе определяется по формуле:

G(дБ) =  (1)

где d_f и d_эт – евклидов просвет кодированной системы и некодированной эталонной системы.

Рис. 2 – Результат работы программной модели декодирования текстового сообщения при значении битового отношения сигнал/шум EbNo=4,5 дБ с использованием жесткого и мягкого алгоритма Витерби

 

В программе метрика d_эт представляет собой количество битовых ошибок между принятым некодированным и исходным сообщением, а метрика d_f представляет собой количество битовых ошибок между принятым кодированным и исходным сообщением, которые вычисляются с помощью команды Матлаб biterr.

Студенты должны написать сами код для реализации данной модели, используя знания, умения и навыки, полученные ими при прохождения практики «Программирование и цифровая обработка сигналов в пакете Матлаб». Разработанная программа оставляет студентам простор для творчества, поскольку к данной программной модели студентам предлагается самостоятельно написать программу графического интерфейса пользователя.

Таким образом, рассмотренная программа позволяет студентам применить на практике знания, полученные при изучении темы помехоустойчивого кодирования, изучаемой в рамках дисциплины «Системы и сети передачи информации».

Список литературы / References

1. Белов Е.Б. Сборник примерных программ учебных дисциплин по направлению подготовки (специальности) 090302 «Информационная безопасность телекоммуникационных систем» (квалификация (степень) «специалист»)/ Е.Б. Белов – М.: МГУПИ, 2011. – 220 с.
2. Помехоустойчивое кодирование. Методы и алгоритмы: Справочник / под. ред. Ю. Б. Зубарева. – М.: Горячая линия –Телеком, 2004. – 126 c.
3. Дворников С.В. Спектрально эффективные сигналы с непрерывной фазой/ С.В.Дворников, С.С.Дворников, С.С. Манаенко и др. // Вестник воронежского государственного технического университета. – 2016. – Т. 12. – № 2. – С. 87–93
4. Федосеев В.Е. Методика и результаты анализа потенциальной помехоустойчивости приема цифрового сигнала на фоне манипулированной структурной помехи/ В.Е.Федосеев, М.С. Иванов // Вестник Воронежского государственного технического университета. – 2010. – Т. 6. – № 11. – С. 108–111
5. Дворников С.В. Помехоустойчивость фазоманипулированных сигналов на основе вейвлетов Гаусса/ С.В.Дворников, С.С.Манаенко// Вестник Воронежского государственного технического университета. –2015. – Т. 11. – № 3. – С. 123–125.
6. Дворников С.В. Синтез манипулированных сигналов на основе вейвлет–функций/ С.В.Дворников, С.С.Дворников, А.М. Спирин // Информационные технологии. – 2013. – № 12. – С. 52–55
7. Hong and K. C. Ho. Classification of BPSK and QPSK signals with unknown signal level using the Bayes technique. in Proc. IEEE ISCAS, 2003, pp. IV.1–IV.4.
8. Panagiotou, A. Anastasoupoulos, and A. Poly–doros. Likelihood ratio tests for modulation classification. in Proc. IEEE MILCOM, 2000, pp. 670 – 674.
9. ViterbiDecoder [Электронный ресурс] – URL: www.mathworks.com/help/comm/ref/viterbidecoder.html (дата обращения: 23.02.2018)
10. Варкасов Р.С. Разработка наглядной математической модели декодера Витерби для детектирования двоичного фазоманипулированного сигнала/ Р.С.Варкасов, И.М. Лернер //Научный Альманах. –2015. – № 8 (10). – С.749–751
11. Чернецова Е.А. «Системы и сети передачи информации» . Часть 1. Телекоммуникационные сети/ Е.А.Чернецова – СПб.: Изд–во РГГМУ. –2013. – 156 с.
12. Скляр Б. Цифровая связь. Теоретические основы и практическое применение/ Б.Скляр. – М.: Вильямс. – 2016. – 1104 с.
13. LLR vs. HardDecisionDemodulation [Электронный ресурс] –URL: www.mathworks.com/help/comm/examples/llr–vs–hard–decision–demodulation.html (дата обращения: 23.02.2018)

Список литературы на английском языке / References in English

1. Belov E.B. Sbornik primernykh programm uchebnykh distsiplin po napravleniyu podgotovki (spetsial'nosti) 090302 «Informatsionnaya bezopasnost' telekommunikatsionnykh sistem» (kvalifikatsiya (stepen') «spetsialist») [Collection of sample programs of educational disciplines in the field of training (specialty) 090302 "Information Security of Telecommunication Systems" (qualification (degree) "specialist")] / E.B. Belov – Moscow: MGUPI, 2011. – 220 p. [in Russian]
2. Pomekhoustoychivoye kodirovaniye. Metody i algoritmy: Spravochnik [Noise immunity coding. Methods and algorithms: Reference book] / under. Ed. Yu. B. Zubarev. – M .: Goryachaya liniya –Telecom, 2004. – 126 p. [in Russian]
3. Dvornikov S.V. Spektral'no effektivnyye signaly s nepreryvnoy fazoy [Spectrally effective signals with a continuous phase] / S.V. Dvornikov, S.S. Dvornikov, S.S. Manaenko and others // Vestnik voronezhskogo gosudarstvennogo tekhnicheskogo universiteta [Bulletin of the Voronezh State Technical University]. – 2016. – T. 12. – No. 2. – P. 87–93 [in Russian]
4. Fedoseev V.E. Metodika i rezul'taty analiza potentsial'noy pomekhoustoychivosti priyema tsifrovogo signala na fone manipulirovannoy strukturnoy pomekhi [The technique and results of the analysis of the potential noise immunity of receiving a digital signal against the background of manipulated structural interference] / V.E. Fedoseev, M.S. Ivanov // Vestnik voronezhskogo gosudarstvennogo tekhnicheskogo universiteta [Bulletin of the Voronezh State Technical University]. – 2010. – T. 6. – No. 11. – P. 108–111 [in Russian]
5. Dvornikov S.V. Pomekhoustoychivost' fazomanipulirovannykh signalov na osnove veyvletov Gaussa [Noise immunity of phase–manipulated signals based on Gauss wavelets] / S.V. Dvornikov, S.S. Mananaenko // Vestnik voronezhskogo gosudarstvennogo tekhnicheskogo universiteta [Bulletin of Voronezh State Technical University]. –2015. – T. 11. – No. 3. – P. 123–125 [in Russian]
6. Dvornikov S.V. Sintez manipulirovannykh signalov na osnove veyvlet–funktsiy [Synthesis of manipulated signals based on wavelet functions] / S.V. Dvornikov, S.S. Dvornikov, А.М. Spirin // Informatsionnyye tekhnologii [Information technology]. – 2013. – No. 12. – P. 52–55 [in Russian]
7. Hong and K. C. Ho. Classification of BPSK and QPSK signals with unknown signal level using the Bayes technique. in Proc. IEEE ISCAS, 2003, pp. IV.1–IV.4.
8. Panagiotou, A. Anastasoupoulos, and A. Poly–doros. Likelihood ratio tests for modulation classification. in Proc. IEEE MILCOM, 2000, pp. 670– 674
9. ViterbiDecoder [Electronic resource] – URL: www.mathworks.com/help/comm/ref/viterbidecoder.html (accessed: 23.02.2018)
10. Varkasov R.S. Razrabotka naglyadnoy matematicheskoy modeli dekodera Viterbi dlya detektirovaniya dvoichnogo fazomanipulirovannogo signala [Development of a visual mathematical model of the Viterbi decoder for detecting a binary phase–shift signal] / R.S.Varkasov, I.M. Lerner // Nauchnyy Al'manakh [Scientific Almanac]. –2015. – No. 8 (10). – P.749–751 [in Russian]
11. Chernetsova E.A. Sistemy i seti peredachi informatsii» . Chast' 1. Telekommunikatsionnyye seti [Information transfer systems and networks. Part 1. Telecommunication networks] / E.A. Chernetsova – SPb .: Izd–vo RGGMU [Publishing house of RSHU]. –2013. – 156 p. [in Russian]
12. Sklar B. Digital Communications. Fundamentials and Applications./ B.Sklar. – M .: Williams. – 2016. – 1104 p. [in Russian]
13. LLR vs. HardDecisionDemodulation – URL: www.mathworks.com/help/comm/examples/llr–vs–hard–decision–demodulation.html (accessed: 02.22.2018)