VIBRATIONS OF ELASTIC HALF-SPACE CONTAINING TWO RADIATING DEFECTS OF FINITE LENGTH

Беркович В.Н.¹, Бабкин А.В.²

¹ORCID: 0000-0003-0915-7170, Доктор физико-математических наук, ²Соискатель, Донской казачий государственный институт пищевых технологий и бизнеса (филиал) «МГУТУ им. К.Г. Разумовского (ПКУ)»

КОЛЕБАНИЯ УПРУГОГО ПОЛУПРОСТРАНСТВА С ДВУМЯ ИЗЛУЧАЮЩИМИ  ДЕФЕКТАМИ  КОНЕЧНОЙ ДЛИНЫ

Аннотация

Работа посвящена рассмотрению задачи динамической теории упругости об установившихся колебаниях, возникающих в массивном упругом теле на начальной стадии предразрушения материала в условиях антиплоской деформации. Колебания генерируются в теле двумя излучающими дефектами. Математическая  постановка вышеуказанной проблемы сводится  к смешанным задачам для уравнения Гельмгольца. Метод решения  основан на их сведении к эквивалентной системе граничных интегральных уравнений. Изучены вопросы разрешимости этих уравнений и установлена структура их решений. Рассматриваемая задача связана с математическим   описанием волновых  полей, возникающих при реализации методов  неразрушающего контроля на основе явления акустической эмиссии.

Ключевые слова: неразрушающий контроль, математическая модель,  смешанная краевая задача, интегральное преобразования, граничное интегральное уравнение.

Berkovich V.N.¹, Babkin F.V.²

¹ORCID: 0000-0003-0915-7170, PhD in Physics and Mathematics, ²Postgraduate student, Don Cossacks’ State Institute of Food Industry and Business (brunch) “MGUTU named after K.G.Razumovsky (FCU)

VIBRATIONS OF ELASTIC HALF-SPACE CONTAINING TWO RADIATING DEFECTS OF FINITE LENGTH

Abstract

The paper is devoted to the study of the dynamic problem of steady vibrations arising in the massive elastic body in the initial pre-destructive stage of its material under antiplane deformation. Vibrations are generated by two radiating defects in the body. Mathematical statement of problem mentioned above is reduced to mixed boundary value problems for Helmholtz equation. The method to find its solution is based on reducing ones to the equivalent system of boundary integral equations. Solvability problem of equations is studied and the structure of its solution is established. The problem in question is connected with mathematical description of wave field when realizing non-destructive testing based on acoustic emission phenomena.

Keywords:  non-destructive testing, mathematical model, mixed boundary value problem, integral transform, boundary integral equation.

В последние годы становится актуальным развитие и применение методов неразрушающего контроля надежности эксплуатации технологического  оборудования предприятий и объектов ответственного назначения в различных отраслях промышленности. Все более актуальными становятся задачи оценки и прогнозирования остаточного ресурса объектов, находящихся в эксплуатации.

Одним из путей решения сформулированной проблемы является мониторинг прочности материала различных элементов оборудования  на ранних стадий его разрушения в процессе эксплуатации с помощью диагностики неразрушающего контроля, основанной на явлении акустической эмиссии [1,2]. Суть метода акустической эмиссии состоит в анализе параметров чрезвычайно слабого ультразвукового излучения, сопровождающего любое изменение либо повреждение (дефект) структуры металлов, их сплавов, композиционных материалов. Существующая аппаратура акусто-эмиссионной диагностики  позволяет регистрировать на свободной поверхности сигналы эмиссии. Установление взаимосвязи между характеристиками сигналов и параметрами диагностируемых дефектов осуществляется на основе построения физико-математических моделей возникающих волновых процессов.

Указанные выше обстоятельства послужили причиной  построения и анализа следующей ниже математической модели.

Будем рассматривать смешанную задачу динамической теории упругости об установившихся колебаниях упругого полупространства Ω с двумя излучающими линейными дефектами, моделируемыми с помощью разрезов J₁, J₂ конечной длины l₁, l₂ и  выходящими на свободную границу Г  полупространства под углами α₁, α₂.  На берегах разрезов 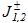 находятся источники гармонических колебаний W(x,y,t) пространственного сдвига  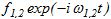с разными частотами ω₁, ω₂ соответственно. В условиях установившихся колебаний требуется восстановить волновое поле во всех точках полупространства Ω.

Математическое моделирование указанного процесса сводится к решению системы дифференциальных уравнений динамической теории упругости (например, [3] и др.), для которых осуществляется постановка смешанной краевой задачи о колебаниях упругого полупространства Ω со свободной границей Г  и двумя излучающими разрезами J_1,2  конечной длины. Представление результирующего колебания в виде

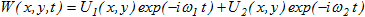   (1)

позволяет свести поставленную задачу к двум однотипным  краевым задачам для уравнения Гельмгольца в Ω с разрезами  и однотипными граничными условиями относительно комплексных амплитуд смещений :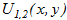

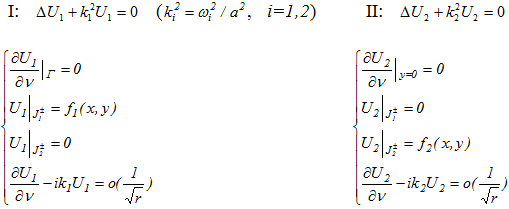  (2)

В соотношениях (2) условие в последней строке представляет условие излучения Зоммерфельда [3]  при 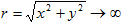 , a - скорость распространения волн сдвига в полупространстве Ω.

Для восстановления требуемого поля смещений  необходимо определить скачки нормальной производной неизвестных функций (безразмерные скачки напряжений) 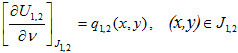 на разрезах J_1,2 в задачах I и II соответственно.  Решения краевых задач  I , II рассматриваются в общем случае как элементы  пространства Соболева  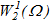 [4].

Метод исследования краевой задач (2) основан на её сведении  с помощью построения функций  Грина 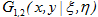 для уравнений Гельмгольца (2). При  этом функции Грина удовлетворяют первому граничному условию задач. Использование представления регулярного решения уравнения Гельмгольца приводит к следующим выражениям комплексных амплитуд смещений  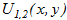полупространства Ω в форме криволинейных интегралов по правым  берегам разрезов :

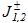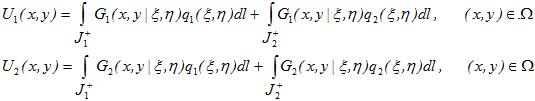  (3)

Устремляя в указанных выше равенствах точку «наблюдения» (x,y) на берега разрезов 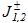 и переходя к локальным координатам r,ρ вдоль берегов разрезов приходим к следующей системе граничных интегральных уравнений, которые для задач I, II  в матрично – векторной форме имеет вид:

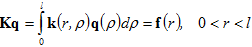  (4)

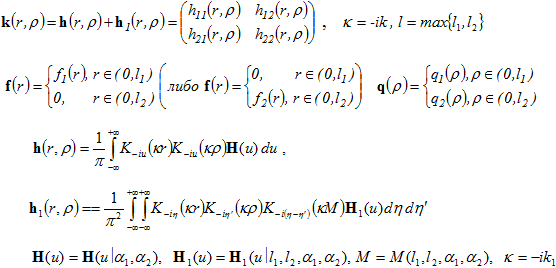  (5)

В процессе получения системы были использованы формулы сложения для бесселевых функций, а также методы интегральных преобразований, связанных с преобразованием Конторовича-Лебедева [4]. Элементы матриц-функций H(u), H₁(u), а также параметра M, в данной работе не приводятся ввиду их громоздкости. В соотношениях (4), (5) функция 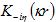 - модифицированная функция Бесселя. Для исследования вопросов разрешимости система (4)  рассматривается предварительно в случае к>0. На основе детального анализа элементов подынтегральной матрицы-функции H(u) устанавливается, что последняя в указанном случае оказывается положительно определенной на действительной оси R¹.

Оператор K левой части  уравнения (2) представляется в виде суммы K=H+H₁, где операторы, действуют в пространствах Соболева-Слободецкого 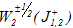 дробной  гладкости. При этом оператор H - однозначно обратим, а оператор H₁ -  компактен, как операторы, действующие в этих пространствах,  что позволяет, согласно теореме Никольского [5], сделать известные заключения о разрешимости интегрального уравнения (4) в случае к>0. Поскольку операторные функции h,h₁, рассматриваемые как функции к в комплексной плоскости 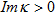, являются аналитическими, то последний результат можно распространить и на случай .

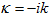В настоящей работе изучена структура решения полученной системы интегральных уравнений (4). Полученные результаты формулируются в виде следующей теоремы.

Теорема. Решение системы (3) представимо в виде:

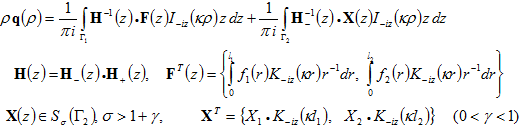  (6)

Контур Г₂ лежит выше Г₁ 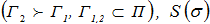, пространство произвольных вектор - функций 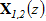,  сходящихся к 0 с весом z^σ в некоторой полосе регулярности, содержащей R¹,  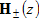- результат факторизации матрицы-функции H(z) относительно R¹. Представление (5) единственно.

Доказательство теоремы основано на результатах [6]. Последующая подстановка решения (6) в уравнение (4) приводит к тому, что неизвестныe векторы 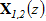 отыскивается из некоторой вспомогательной системы интегральных уравнений второго рода  с вполне непрерывным оператором в пространстве функций .

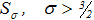При этом оказывается, что построенное таким образом решение q(ρ) в форме (5) принадлежит пространству дробной гладкости 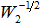, что вполне согласуется с известными свойствами граничных значений нормальных производных функций рассматриваемых как элементы  пространства Соболева 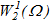. Полная непрерывность оператора системы позволяет представить его в виде  суммы конечномерного и малого, что применять различные численные методы для решения системы интегральных уравнений, а, следовательно,   и для решения исходной краевой задачи.

Восстановление волнового поля во всем полупространстве с дефектами осуществляется на основе формулы (1) с помощью интегральных представлений  регулярного решения уравнения Гельмгольца (3) и решения (6) граничных интегральных уравнений (4). Для восстановления волнового поля свободной поверхности необходимо в формулах (3) точку (x,y) устремить на свободную поверхность Г полупространства.

Предлагаемый подход может быть использован также и в случае наличия произвольной системы излучающих дефектов, не выходящих на свободную границу, а расположенных внутри массивного тела, моделируемого упругим полупространством.

 

Список литературы / References

1. Буйло С.И. Диагностика предразрушающего состояния материалов по параметрам амплитудного распределения сигналов сопутствующего акустического излучения. – Дефектоскопия, 2012, № 11, С. 32-45.
2. Builo S.I. Physical, Mechanical and Statistical Aspects of Acoustic Emission Diagnostics. In: Physics and Mechanics of New Materials and Their Applications. New York: Nova Science Publishers. Chapter 15. – 2013. –444 p.
3. Рекач В.Г. Руководство к решению задач по теории упругости. – М. Высшая школа, 1977. – 275с.
4. Лебедев Н.Н. Специальные функции и их приложения. – М.–Л.Наука.
5. – 358с.
6. Бесов О.В., Ильин В.П., Никольский С.М. Интегральные представления функций и теоремы вложения. – М. Наука. 1975. – 478с.
7. Беркович В.Н. О точном решении одного класса интегральных уравнений смешанных  задач упругости и математической физики.// Докл. АН СССР. –1982. –Т.267. –№2.  –С.327– 330.

Список литературы на английском языке / References in English

1. Builo S.I. Diagnostika predrazrushayuschego sostoyaniya materialov po parametram amplitudnogo raspredeleniya signalov soputstvuyuschego akusticheskogo izlucheniya. [Pre-destuctive testing of state of materials based on parameters of amplitude signal distribution of the attendent acoustic emission ]  – Дефектоскопия, [Non-destructive testing]. –2012. –№ 11. –С. 32–45.[in Russian]
2. Builo S.I. Physical, Mechanical and Statistical Aspects of Acoustic Emission Diagnostics. In: Physics and Mechanics of New Materials and Their Applications. New York: Nova Science Publishers. Chapter 15. – 2013. –444 p.
3. Rekach V.G. Rukovodstvo k resheniyu zadch po teorii uprugosti [The Guide to Solve Elasticity Problems] / V.G. Rekach – М.: Visshaya shkola.[“Higher School” Press] –1977. –275 P. [in Russian]
4. Lebedev N.N. Spetzialniye funktzii i ih  prilogeuiya.[Special Functions and its Applications] – М.-L.: Nauka.[“Science” Press] –1968. – 358 P. [in Russian]
5. Besov O.V., Ilyin V.P., Nikolskiy S.M.. Integralniye predstavleniya funktziy i teoremi vlogeniya.[Integral Representation of Functions and Embedding Theorems] –М. Nauka. .[“Science” Press]. 1975. – 478 P. [in Russian]
6. Berkovich V.N. O tochnom reshenii odnogo klassa integralnih uravneniy  smeshannih zadach uprugosti i matematicheskoy  fiziki. [On the Exact Solution of Some Class of Integral Equations for Mixed Problems of Elasticity and   Mathematical Physics] /V.N.Berkovich // Dokladi Akademii Nauk SSSR. [Reports of Academy of Sciences]. –1982. –V.267. –№2. – P. 327– 330. [in Russian]