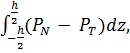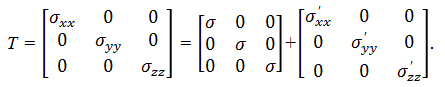MECHANISM OF FORMATION OF SURFACE LIQUID TENSION

Готовцев В.М.¹, Сухов В.Д.², Сазонов А.И.³

¹Профессор, доктор технических наук, ²Профессор, кандидат химических наук, ³Доцент, кандидат исторических наук, Ярославский государственный технический университет

МЕХАНИЗМ ФОРМИРОВАНИЯ ПОВЕРХНОСТНОГО НАТЯЖЕНИЯ ЖИДКОСТИ

Аннотация

В статье предложен новый подход к описанию поверхностных явлений, возникающих на границе раздела различных фаз. Напряженное состояние среды в точках межфазного слоя представлено тензором напряжений, включающим шаровую и девиаторную части. Шаровая часть тензора определяется давлением среды в изотропном состоянии, девиаторная часть формируется силами межмолекулярного взаимодействия. Напряжения, формирующие поверхностное натяжение жидкости, представляют собой девиаторные компоненты тензора межфазных напряжений.

Ключевые слова: поверхностное натяжение, шаровая и девиаторная части тензора межфазных напряжений.

 

Gotovcev V.I.¹, Suhov V.D.², Sazonov A.I.³

¹ Professor, PhD in Engineering, ² Professor, PhD in Chemistry, ³ Associate professor, PhD in History, Yaroslavl State Technical University

MECHANISM OF FORMATION OF SURFACE LIQUID TENSION

Abstract

This paper proposes a new approach to the description of surface phenomena occurring at the interface between different phases. Stress state of the environment at the points of the interfacial layer is represented by the stress tensor, including spherical and deviatoric part. Ball of the tensor determined by the pressure medium in the isotropic state deviator portion formed intermolecular forces. Stresses that form the surface tension of the liquid, are deviatoric tensor components of interfacial stresses.

Keywords: surface tension, and the ball of the deviator stress tensor interphase.

 

Современные подходы к описанию поверхностных явлений на границах раздела фаз условно можно разбить на две большие группы. Классический подход, базирующийся на механистических представлениях Юнга и Лапласа, разработанных более двухсот лет назад, до настоящего времени составляет основу большинства инженерных расчетов. Однако при более тщательном рассмотрении этих явлений обнаруживается, что в сложившуюся систему представлений заложены довольно грубые допущения. Для инженерных расчетов на современном уровне оказываются необходимыми устранение погрешностей и уточнение схемы описания поверхностных эффектов [1].

Современные модели поверхностных явлений основаны на особенностях межмолекулярных взаимодействий, общей чертой которых является их флуктуационное электромагнитное происхождение [2]. Круг вопросов, связанных проблемой их описания чрезвычайно широк и с трудом поддаются обобщению и выработке единых подходов. Даже в учебной литературе по теоретической физике отдельные вопросы теории межмолекулярного взаимодействия рассматриваются в разных курсах, таких, как нерелятивистская квантовая механика, квантовая электродинамика, квантовая теория поля, теория конденсированного состояния и электромагнитных флуктуации [2].

Впервые теоретическое выражение для определения коэффициента поверхностного натяжения жидкости было получено Баккером  Оно основано на представлении жидкости сплошной средой, которая в межфазном поверхностном слое обладает свойством анизотропии. Формула Баккера для определения поверхностного натяжения γ записывается в виде:

γ =                                             (1)

где h – толщина межфазного слоя,  – нормальная составляющая тензора давления,  – тангенциальная составляющая тензора.

Анизотропия среды проявляется в различии компонент тензора напряжений, трактуемого как тензор давления. В современном представлении тензор давления включает три равные по величине компоненты, значения которых не зависят от расположения контрольной площадки. В соответствии с этим возникает вопрос о том, что понимается под составляющими давления в выражении (1) и чем обусловлена разница их значений.

Традиционно в механике сплошной среды напряженное состояние в точке представляется в виде тензора напряжений, значения компонент которого, определяются действием внешних сил, приложенных к рассматриваемому объему среды. При этом, равновесие текучих сред предполагает выполнение закона Паскаля: давление, производимое на покоящуюся жидкость или газ, передается в любую точку жидкости или газа одинаково по всем направлениям . Таким образом, под давлением следует понимать тензор напряжений с тремя одинаковыми диагональными компонентами. Исходя из этого, компоненты тензора в уравнении (1) не является давлениями.

Представим напряженное состояние среды в межфазном слое как результат наложения силового поля межмолекулярного взаимодействия на изотропное поле давления. Значение давления в рассматриваемой точке межфазного слоя равно давлению среды при заданном значении удельного объема среды в изотропном состоянии. Представим тензор напряжений суммой тензоров двух видов. Тензор первого вида определяет изотропные свойства среды, т.е. представляет совокупность компонент, формирующих давление, удовлетворяющее закону Паскаля. Компоненты второго тензора определяют анизотропные свойства силового поля и обусловлены действием объемных сил. Такое представление тензора достаточно широко используется в механике сплошных сред, например  и осуществляется посредством следующих зависимостей:

    (2)

Компоненты записанного тензора Т должны удовлетворять соотношениям:

                      (3)

Первый тензор в правой части выражения (3) с одинаковыми компонентами  определяет изотропное давление Р в среде, а тензор, компоненты которого обозначены штрихами, называется девиатором напряжений.

Отметим, что такое представление напряженного состояния среды не является формальным представлением одного из возможных способов записи, но содержит вполне определенный физический смысл. В качестве подтверждения можно привести простой пример. Если взять твердый образец цилиндрической формы и приложить к основаниям цилиндра достаточно большие сжимающие напряжения, то в результате деформации образец примет бочкообразную форму. Это свидетельствует о формировании в материале образца растягивающих напряжений в плоскости, перпендикулярной направлению сжатия, приводящих к выпучиванию боковой поверхности цилиндра.

Проведем аналогию с напряженным состоянием среды в межфазном слое жидкость – газ, в котором сжимающие напряжения формирует объемная сила молекулярного притяжения, направленная в сторону жидкой фазы. Выберем систему координат таким образом, чтобы ось Z была направлена перпендикулярно к межфазному слою. Тогда сжимающие напряжения , обусловленные действием межмолекулярных сил, в соответствии с выражениями (4), приведут к образованию нормальных напряжений  и , действующих в плоскости межфазного слоя и формирующих поверхностное натяжение.

Напряженное состояние среды обладает симметрией относительно оси Z. Компоненты тензора напряжений в плоскости слоя будут равны, т.е.  =   и  = , а девиаторная компонента тензора , обусловленная действием объемной силы межмолекулярного притяжения, в соответствии с выражением (4), должна иметь противоположный знак. Таким образом, формирование сжимающей компоненты тензора  приводит к появлению растягивающих напряжений  и , действующих в плоскости межфазного слоя и формирующих поверхностное натяжение жидкости. В соответствии с этим рассмотренное ранее условие равновесия среды  = const принимает форму постоянства по толщине слоя значения нормальной компоненты тензора межфазных напряжений:

 = Р +  = const.                                      (4)

Отсюда следует, что изменение давления Р = σ в межфазном слое компенсируется девиаторной компонентой   тензора межфазных напряжений.

В соответствии с уравнениями (3) и (4) напряженное состояние среды в точках межфазного слоя определяется тензором со следующими компонентами:

;  ;  .               (5)

В записанных выражениях Р = Р(V) определяет шаровую часть тензора межфазных напряжений, т.е. давление в рассматриваемой точке межфазного слоя со значением удельного объема V. Другими словами это давление в изотропной среде при заданном значении удельного объема, определяемое уравнением состояния среды. Из симметрии напряженного состояния относительно оси Z следует, что . Определив распределение рассмотренных компонент тензора межфазных напряжений по толщине слоя, т.е. их зависимость от координаты Z, можно найти поверхностное натяжение жидкости, как:

γ =                                                  (6)

Таким образом, рассмотренное представление тензора межфазных напряжений среды в межфазном слое позволяет выявить механизм формирования поверхностного натяжения жидкости, основанный на представлениях механики сплошной среды.

Литература

1. Иголкин С.И. Критический анализ опытов по измерению углов смачивания и сил поверхностного натяжения // Прикладная физика. –2007. –№ 4. –С. 43-51.
2. Бараш Ю.С. Силы Ван-дер-Ваальса. М.: Наука, 1988. 344 с.
3. Bakker G. Kappillarität und Oberflächengspspannung: Handbuch der Experimental Physik. Leipzig, Bd. 6.
4. Лойцянский Л.Г. Механика жидкости и газа. М.: Наука, 1978. 736 с.
5. Виноградов Г.В., Малкин А.Я. Реология полимеров. М.: Химия, 1977. 438 с.

References

1. Igolkin S.I. Kriticheskij analiz opytov po izmereniju uglov smachivanija i sil poverhnostnogo natjazhenija // Prikladnaja fizika, –2007. –№ 4. –S. 43-51.
2. Barash Ju.S. Sily Van-der-Vaal'sa. - M.: Nauka, 1988. 344 s.
3. Bakker G. Kappillarität und Oberflächengspspannung: Handbuch der Experimental Physik. Leipzig, 1928. Bd. 6.
4. Lojcjanskij L.G. Mehanika zhidkosti i gaza. M.: Nauka, 1978. 736 s.
5. Vinogradov G.V. Malkin A.Ja. Reologija polimerov. M.: Himija, 1977. 438 s.