THE ABRIKOSOV VORTICES CONTAINING MULTIPLE FLUX QUANTA OF THE MAGNETIC FIELD
Тихомиров И.В.
Кандидат физико-математических наук,
Омский государственный технический университет
ВИХРИ АБРИКОСОВА, СОДЕРЖАЩИЕ НЕСКОЛЬКО КВАНТОВ ПОТОКА МАГНИТНОГО ПОЛЯ
Аннотация
В работе исследован одиночный вихрь в тонкой сверхпроводящей плёнке, содержащий несколько квантов потока. Получено точное выражение для свободной энергии вихря с учётом распределения параметра порядка вблизи сердцевины вихря. Показано, что возможно слияние вихрей, содержащих один квант потока, в плотной вихревой жидкости.
Ключевые слова: вихревая жидкость, сверхпроводящая плёнка, вихрь Абрикосова, сверхпроводник второго рода.
Tikhomirov I.V.
PhD in Physics and mathematics,
Omsk State Technical University
THE ABRIKOSOV VORTICES CONTAINING MULTIPLE FLUX QUANTA OF THE MAGNETIC FIELD
Abstract
In this paper, we investigated a single vortex in a thin superconducting film containing multiple flux quanta. Obtained the exact expression for the free energy of the vortex taking into account the distribution of the order parameter near the core of the vortex. It is shown that the merging of the vortices containing one quantum of flux, in a dense swirl of liquid.
Keywords: vortex liquid, superconducting film, the Abrikosov vortex, the superconductor of the second kind.
В тонких плёнках сверхпроводника второго рода, при внешнем магнитном поле близком к Hc2, образуется многовихревое состояние. При этом характерное расстояние изменения параметра порядка составляет несколько длин когерентности. Магнитное поле, напротив, из-за слабой экранировки в тонкой плёнке практически однородно и изменяется только на макроскопических расстояниях.
Известно, что в объемном сверхпроводнике выгоднее образовываться вихрям, содержащим один квант потока магнитного поля. Вихрь, содержащий два и более квантов потока имеет большую энергию и невозможен в объемном сверхпроводнике.
В тонких плёнках энергия взаимодействия вихрей определяется не магнитным полем, как это происходит в объемном сверхпроводнике, а энергией нормальных сердцевин вихрей, которая определяется распределением параметра порядка. Эта энергия существенно меньше, поэтому в тонких плёнках слияние не приводит к существенному росту их энергии, и в случае их движения в вихревой жидкости могут образовываться вихри, содержащие два и более квантов потока.
Потенциал Гиббса сверхпроводника во внешнем магнитном поле GS можно записать как
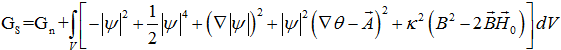(1)
где ψ – комплексный параметр порядка теории Гинзбурга–Ландау, 
– векторный потенциал, 
– параметр Гинзбурга–Ландау, – индукция магнитного поля, – напряженность внешнего магнитного поля, Gn – свободная энергия нормального состояния. Величины Gs и Gn нормированы на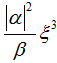 
, где α, β – константы теории Гинзбурга–Ландау, а 
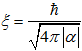– длина когерентности, координаты нормированы на ξ. Параметр порядка ψ записан в амплитудно–фазовом представлении, т.е. 
. Величины 
нормированы соответственно на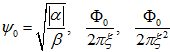 
, причем 
, а 
– квант потока магнитного поля.
При переходе от объемного сверхпроводника к тонкой плёнке (d<<λ, d – толщина плёнки) экранировка магнитного поля ослабевает. В этом случае можно ввести эффективную длину экранировки [1]:
.
Т.е. в тонких сверхпроводящих плёнках распределение магнитного поля достигает макроскопических размеров.
При рассмотрении движения нескольких вихрей в области размером много меньше λ2d слагаемое 
в формуле (1) не меняется. Оно представляет собой энергию Гиббса, связанную с магнитным полем GM. При H0>Hc1, т.е. при наличии вихрей, это слагаемое отрицательно.
Также же покажем, что 
. Для этого рассмотрим одиночный вихрь, содержащий n квантов потока магнитного поля. Вычислим поток, который создает вихрь через площадь круга с центром в центре вихря и радиусом ρ:
.
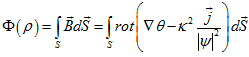Здесь использовано уравнение Гинзбурга-Ландау
(2)
где 
– сверхпроводящая плотность тока, нормированная на 
. Координаты также нормированы на ξ, поток нормирован на 
.
Используя теорему Стокса, получим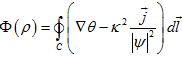 
, где C – окружность радиуса ρ. Для одиночного вихря, несущего n квантов потока, фаза параметра порядка θ=nφ, где φ – полярный угол, имеем: 
.
Другой стороны, поскольку магнитное поле существенно меняется на расстояниях порядка λ2d>>ξ, то магнитное поле однородно вплоть до расстояния ρ, если ρ<<λ2d. В нормированных координатах это условие превращается в 
. В этом случае поток пропорционален площади круга, т.е. 
, где 
– среднее магнитное поле вблизи вихря, Sпл – площадь плёнки, n – число квантов потока магнитного поля через плёнку, 
– поле в центре вихря с одним квантом потока [2].
Учитывая, что плотность тока 
, получим
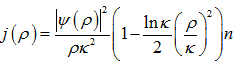
При условии (для ненормированных переменных ρ<<λ2d), вторым слагаемым в скобках можно пренебречь, тогда 
.
Сравнивая это выражение с (2) и учитывая, что 
, получаем, что 
при условии 
. Кроме того, при наличии большого числа случайно расположенных вихрей 
при n>>1. Тогда потенциал Гиббса тонкой сверхпроводящей плёнки небольшого размера (l<< λ2d) будет равен:
,
а соответствующее уравнение Гинзбурга-Ландау имеет вид:
.
В полярных координатах для одиночного вихря уравнение Гинзбурга-Ландау примет вид:
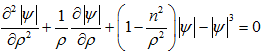(3)
Проведенное численное решение уравнения (3) с граничными условиями |ψ(0)|=0 и |ψ(∞)|=1 показало, что результат для n=1 совпал c решением этого же уравнения, представленного в работе [2].
Результаты решения для n>1 были использованы для нахождения F – свободной энергии (на единицу длины) вихрей, содержащих несколько квантов потока:
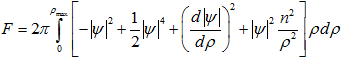. (4)
Последнее слагаемое представляет собой свободную энергию сверхпроводящего тока вихря и при ρmax>>1, |ψ|→1 на верхнем пределе имеет логарифмическую расходимость. На нижнем пределе расходимости нет, т.к. в нормальной сердцевине вихря |ψ|=0 и сверхпроводящий ток отсутствует. Остальные слагаемые выходят на постоянное значение при увеличении ρmax. Численное интегрирование уравнения (4) показало, что свободная энергия подчиняется закону 
.
Переходя к ненормированным величинам, получим для вихря единичной длины:
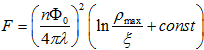. (5)
Учитывая, что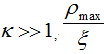 
можно заменить на κ. Сравнивая полученное выражение с выражением для свободной энергии вихря с одним квантом потока [3]:
,
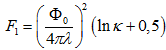получим, что константа в формуле (5) равна 0,5. Отметим, что в статье [2] для этой же константы получено значение 0,497, т.е. можно записать, что
,
где F1 – свободная энергия вихря, содержащего один квант потока.
Таким образом, при больших плотностях вихрей в тонких плёнках возможно динамическое слияние двух вихрей, содержащих по одному кванту потока, в один, содержащий два кванта потока. При этом энергия вихрей увеличивается на величину, равную разности свободных энергий этих состояний ΔF. Магнитная энергия GM при этом не изменится, поскольку речь идёт о перемещении вихрей на расстояние в несколько ξ. Существенное изменение магнитной энергии произойдёт только при перемещении вихрей на расстояния порядка λ2d>>ξ. Таким образом, магнитная энергия вихря, содержащего два кванта потока, равна магнитной энергии двух вихрей, содержащих по одному кванту потока и находящихся на небольшом расстоянии друг от друга. То же можно сказать про энергию тока на больших расстояниях, т.е. логарифмическая расходимость этих двух состояний будет одинакова, тогда:
,
Это небольшая энергия по сравнению с полной энергией вихрей, поэтому такой барьер может легко преодолеваться и приводить к слиянию вихрей. Подобным образом могут образовываться вихри, содержащие три и более квантов потока.
Таким образом, мы приходим к выводу, что в тонких плёнках при внешнем магнитном поле близком к Hc2, в вихревой жидкости могут присутствовать вихри, содержащие два и более квантов магнитного поля.
Литература
- Де Жен П.Сверхпроводимость металлов и сплавов. – М.: Мир, 1968.
- Hu C.R., Phys.Rev. B, 6, 1972, p. 1756.
- Шмидт В.В. Введение в физику сверхпроводников. – М.:МЦНМО, 2000.
References
- De Zhen P.Sverhprovodimost' metallov i splavov. – M.: Mir, 1968.
- Hu C.R., Phys.Rev. B, 6, 1972, p. 1756.
- Shmidt V.V. Vvedenie v fiziku sverhprovodnikov. – M.:MCNMO, 2000.