PARALLEL ALGORITHMS FOR LOCAL VARIATION METHOD FOR OPTIMAL CONTROL PROBLEMS

Карамова А.И.¹, Петров Д.А.²

¹Кандидат физико-математических наук,

Башкирский государственный университет

ПАРАЛЛЕЛЬНЫЙ АЛГОРИТМ МЕТОДА ЛОКАЛЬНЫХ ВАРИАЦИЙ ДЛЯ ЗАДАЧИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ

Аннотация

В статье рассмотрена технология решения задачи оптимального управления в виде параллельного итерационного процесса оптимизации с выбором наилучшего приближения. Данный алгоритм проверен на тестовых примерах с известными аналитическими решениями.

Ключевые слова: оптимальное управление, параллельные технологии.

Karamova A.I.¹, Petrov D.A.²

¹Candidate of Physical and Mathematical Sciences,

Bashkir State University

PARALLEL ALGORITHMS FOR LOCAL VARIATION METHOD FOR OPTIMAL CONTROL PROBLEMS 

Abstract

The article describes the technology for solving the problem of optimal control in the form of parallel optimization processes with the choice of the best approximation. This algorithm is tested on test cases with known analytical solutions.

Keywords: optimal management, parallel technology.

Решение задач оптимального управления численными способами, сопровождается большим количеством вычислений, что соответственно влияет на время ожидания результата. В некоторых ситуациях, нет привилегий на расточительность времени, нужны быстрые и точные ответы от используемых алгоритмов. К счастью научный прогресс не стоит на месте. Старые одноядерные компьютеры вытесняются более производительными многоядерными. Но и эта тенденция не проживет долго. На пороге нашего мира в роль вступают кластерные системы, основанные на большом количестве процессоров. Сила таких систем заключена в том - что алгоритмы выполняются параллельно, тем самым давая колоссальный прирост производительности. Многие последовательны алгоритмы решения прикладных задач, дают возможность изменить свою структуру и ложатся на параллельные архитектуры.

Целью данной работы является разработка и оптимизация алгоритма метода вариаций для решения задачи оптимального управления на системах с большим количеством вычислительных ядер.

Запишем формулировку задачи оптимального управления. Дана система (объект, процесс), состояние которой описывается дифференциальным уравнением:

,

где  x – вектор фазовых координат, u – вектор управления, t – время.

На вектора x и u наложены ограничения xÎ X, uÎ U.

Система рассматривается на интервале tÎ [0, T].

Требуется определить вектор–функции u(t), x(t) доставляющие минимум функционалу J=J(x, u) при переводе из начального состояния (x(0), 0) в конечное  состояние (x(T), T).

Задачи оптимального управления классифицируются по способу задания функционала, по способу задания ограничений вдоль траектории и по способу задания краевых условий.

Не останавливаясь подробно на изложением общего материала, перейдем у частному методу численного решения задачи оптимального управления, а именно на методе локальных вариаций. Алгоритм последовательного метода представлен на рис.1.

Суть метода распараллеливания довольна проста – «разделяй и властвуй». Элементарная операция выполняется для каждой точки начального оптимального управления. Тем самым для каждой точки решается  система дифференциальных уравнений одним из численных методов.

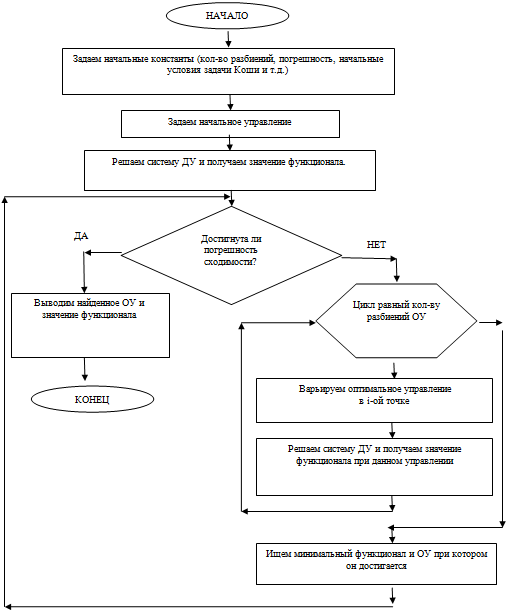Рис. 1 – Блок-схема последовательного алгоритма (CPU) поиска оптимального управления

По мере роста размера разбиений оптимального управления, растет количество однотипных вычислений. Целью работы является сведение всех однотипных вычислений в блок выполняемый за одну итерацию. То есть элементарные операции выполняются не друг за другом, а параллельно независимо друг от друга (рис. 2).

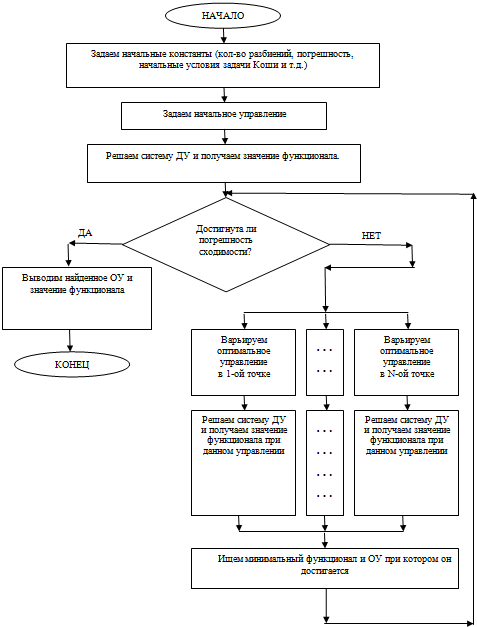Рис. 2 – Блок-схема параллельного  алгоритма (GPU) поиска оптимального управления

Далее приведены таблицы и диаграммы сравнения производительности двух вариантов алгоритмов поиска оптимального управления на тестовом примере с известным аналитическим решением.

Пример. Даны модель объекта управления:

с начальными условиями  и функционал 

Требуется найти оптимальное программное управление  и соответствующую ему траекторию .

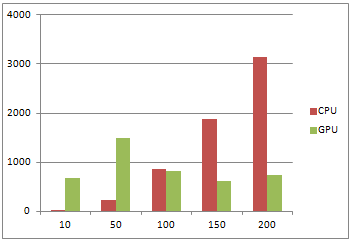
Таблица 1

Разбиений	Итераций	CPU	GPU
10	100	16	686
50	100	234	1498
100	100	858	812
150	100	1872	624
200	100	3135	734

Рис. 3 – Диаграмма 1

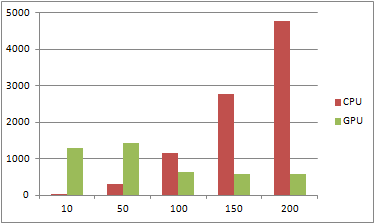
Таблица 2

Разбиений	Итераций	CPU	GPU
10	150	32	1295
50	150	312	1436
100	150	1170	624
150	150	2787	593
200	150	4787	594

Рис. 4 – Диаграмма 2

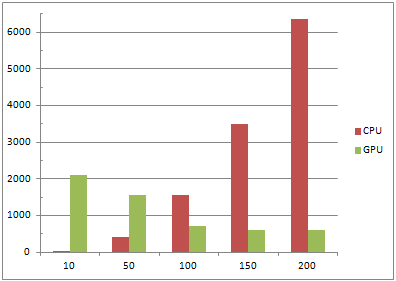
Таблица 3

Разбиений	Итераций	CPU	GPU
10	200	31	2106
50	200	405	1560
100	200	1560	702
150	200	3500	608
200	200	6361	608

Рис. 5 –Диаграмма 3

Из приведенных данных видим: при малом количестве разбиений, последовательный алгоритм выполняется намного быстрее параллельного, но имеет большую зависимость от количества итераций. При увеличении числа итераций значительно меняется время выполнения алгоритма. При работе параллельного алгоритма видим, что на время счета сильно не влияет количество итераций, но при малом количестве разбиений параллельный алгоритм просто не успевает разогнать мультипроцессор и поэтому при малых количествах разбиений он проигрывает своему конкуренту. Таким образом при большом количестве итераций и малом шаге разбиений параллельный алгоритм работает более стабильно и значительно быстрее, что подтверждает эффективность использования подобных алгоритмов.

Литература

1. Вержбицкий В.М. Основы численных методов. – М.: Высшая школа, 2002.
2. Киреев В.И., Пантелеев А.В. Численные методы в примерах и задачах. – М.: Высшая школа, 2008.
3. Перепёлкин Е.Е., Садовников Б.И., Иноземцева Н.Г. Вычисления на графических процессорах (GPU) в задачах математической и теоретической физики. – М.: URSS, 2014.
4. Сандерс Д., Кэндрот Э. Технология CUDA в примерах. - М.: ДМК Пресс, 2011.

References

1. Verzhbickij V.M. Osnovy chislennyh metodov. - M.: Vysshaja shkola, 2002.
2. Kireev V.I., Panteleev A.V. Chislennye metody v primerah i zadachah. - M.: Vysshaja shkola, 2008.
3. Perepjolkin E.E., Sadovnikov B.I., Inozemceva N.G. Vychislenija na graficheskih processorah (GPU) v zadachah matematicheskoj i teoreticheskoj fiziki. - M.: URSS, 2014.
4. Sanders D., Kjendrot Je. Tehnologija CUDA v primerah. - M.: DMK Press, 2011.