INTERPRETATION OF DATA FROM THE RHEOLOGICAL MODULE ‘TENSIOMETER DSA-100’
INTERPRETATION OF DATA FROM THE RHEOLOGICAL MODULE ‘TENSIOMETER DSA-100’
Abstract
The work is dedicated to the surface rheology of solutions of organic substances. On the basis of experimental data, the analysis of phase shifts between the rheological curves of surface tension and surface area of an oscillating drop has been carried out. It is shown that in low-viscosity liquids (propanol-2, distilled water and chlorophyll solution) the dilatation of the surface tension of the oscillating drop is in the frequency range from 1 to 2 Hz.
The threshold frequency of hovering drop oscillation for propanol-2 at which the periodicity of nonequilibrium surface tension is demonstrated is established.
The dependence of the phase shift between the sinusoidal curves of surface tension and the area of an oscillating drop on the shear rate and the concentration of organic components in solutions has been studied. The obtained nonlinear rheological properties of the systems allow to determine the viscoelastic parameters of the studied liquid.
1. Введение
Свойства композиционных полимерных материалов во многом определяются их матрицей, в структуре которой выделены параметры давления и температуры, оказывающие влияние на связующие реологические зависимости. Работа посвящена изучению сдвигов между кривыми поверхностного натяжения (ПН) и площади осциллирующей висящей капли, а также определению модуля вязкости и эластичности раствора хитозана (ХТЗ) . Для изучения явления поверхностной реологии применяется простой и надежный в работе метод висящей осциллирующей капли. Поверхностная эластичность и вязкость обуславливают стабильность эмульсии пен. Параметры поверхностной реологии ХТЗ-вых систем включают вязкость, модуль упругости и время релаксации, изученные для неравновесных молекулярных растворов , . Существующие модели для прогнозирования поверхностных реологических свойств полимерных растворов недостаточно точны в контексте растворов ХТЗ, что приводит к расхождениям в однородности и механической стабильности покрытий. Целью данного исследования является разработка прогностической модели для поверхностной реологии растворов ХТЗ, включающей влияние концентрации и температуры, и оценка ее точности путем сравнения прогнозируемых значений с экспериментальными измерениями. Это позволит оптимизировать процессы нанесения покрытий, что приведет к улучшению свойств материалов и снижению производственных затрат. Изучение дилатационной реологии поверхности ограничено существующими экспериментальными методами и традиционными методами измерения поверхностного натяжения, которые недостаточны для растворов полимеров из-за медленного установления равновесия и слабой зависимости от концентрации , . Актуальность исследования поверхностной реологии раствора ХТЗ обусловлена важностью понимания их механических свойств, таких как модуль вязкости и модуль эластичности. Эти параметры играют ключевую роль в различных областях науки и техники, включая материалы, фармацевтику и пищевую промышленность .
Данная работа нацелена на исследование взаимосвязи между вязкоупругими свойствами ньютоновских и неньютоновских жидкостей при различных режимах деформации, а также определению порога динамической вязкости в спиртосодержащих растворах.
2. Основные результаты
2.1. Теоретическая часть
Реологические свойства необходимо учитывать при решении задач, связанных с такими прикладными направлениями, как механика твердых деформируемых объектов, а также механики и гидромеханики, в том числе и биомеханики.
При изучении поверхностной реологии рассчитывают 2 параметра, характеризующие поведение поверхности: модуль эластичности и модуль вязкости. Модуль эластичности пропорционален размеру деформации поверхности, а модуль вязкости – скорости расширения или сжатия поверхности. Для исследования реологии поверхности и получения данных модулей (эластичности и вязкости) применяется метод висящей капли, реализованный на тензиометре DSA-100.
Тензиометр DSA-100 (Рис. 1) с реологическим модулем включает электронный шприц-модуль для создания осциллирующих капель на конце рабочего капилляра. Исследуемая жидкость поступает в капилляр посредством пьезонасоса, контролируемый компьютером. Возвратно-поступательные перемещения в исследуемой жидкости порождают синусоидальные колебания площади ПН. Программное обеспечение анализирует изменения межфазного натяжения, которое вызвано синусоидальным увеличением и уменьшением площади поверхности капли. Из анализа фазового сдвига между соседними кривыми рассчитываются модуль вязкости и модуль эластичности.
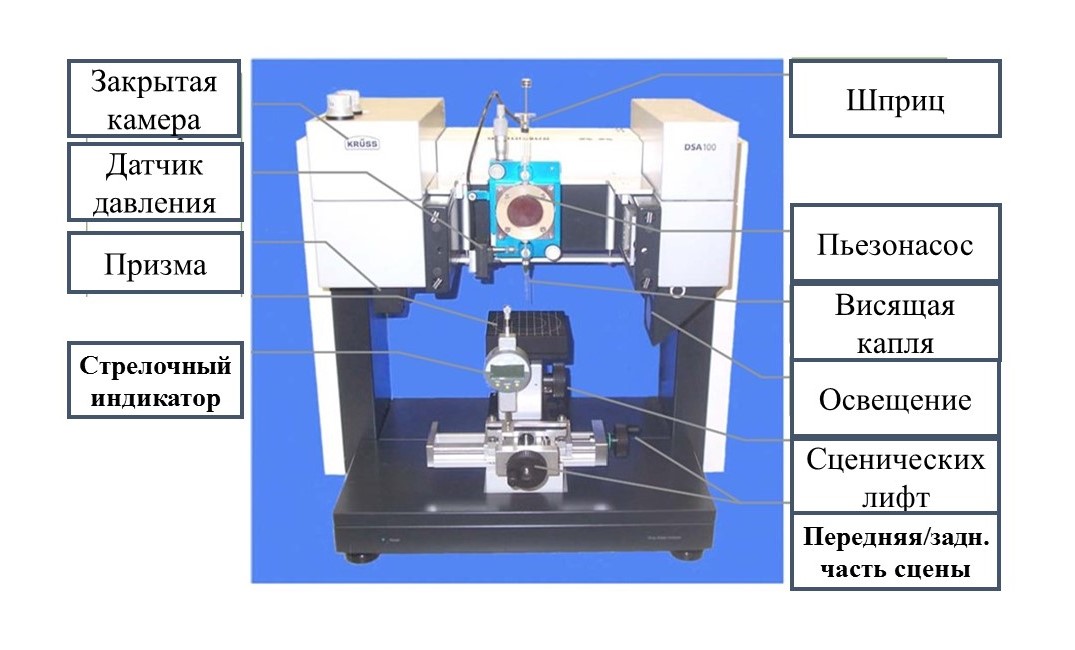
Рисунок 1 - Тензиометр DSA-100
Вязкость ньютоновской жидкости не зависит от приложенного напряжения сдвига, что наглядно изображено на (Рис. 2), т. к. внутреннее сопротивление между компонентами жидкости незначительно. Поэтому скорости релаксации молекул летучих жидкостей значительны и такие системы являются низковязкими. Высоковязкие жидкости имеют медленное течение из-за наличия сил трения между плотно расположенными молекулами.
2.2. Экспериментальная часть
Руководствуясь техническим описанием реологического модуля, были проведены эксперименты по изучению кривых, полученных при осцилляции, капли исследуемой жидкости (пропанола-2). Анализ полученных данных устанавливает закономерность поведения кривых межфазного натяжения от периодически изменяющегося объема осциллирующей капли пропанола-2. Таким образом, показано, что периодичность величины ПН у летучих ньютоновских жидкостей (пропанол-2, дегазированная вода) не регистрируется используемым реологическим модулем DSA-100 в диапазоне частот меньше 1 Гц (Рис. 1, 2). Непериодичность функции ПН в области низких частот объясняется высокой скоростью релаксации молекул спирта. Для получения периодических кривых ПН чистых компонентов (вода, пропанол-2) необходимо измерения проводить на более высоких частотах . Настройка параметров системы частотного диапазона позволила получить дилатационные реологические кривые ньютоновских жидкостей (дистиллированная вода, спирт-пропанол-2).
Для объяснения поверхностных явлений, происходящих во время дилатации, подвешенной капли необходимо учитывать свойства эластичности и вязкости исследуемой жидкости.
Согласно формуле (1) параметры вязкости пропанола-2 при температуре 23 0 С имеют следующие приближенные равенства:
где динамическая вязкость пропанола-2 составляет ~ 0,002038 Па∙с, а его плотность ~ 785,1 кг/м3. Тогда кинематическая вязкость равна ν =2,59∙10-6м2/с, что характерно для маловязких жидкостей , .
В системе DSA-100 параметры видеокамеры ограничены 25 кадрами в секунду. Следовательно, оптические и осциллирующие периоды капли менее одной секунды устанавливать не имеет смысла, потому как количество кадров будет меньше оптимально подобранного оптического периода равной 2с.
На рисунке 2 показано сравнение неравновесного ПН и площади осциллирующей капли во времени t. Как видно из графика, ПН пропанола-2 не является периодической функцией на частоте колебания капли равной 0,5 Гц. Данный фактор статистической независимости величины ПН при осцилляции объема пропанола-2 был экспериментально изучен путем фиксирования минимального и максимального объемов капли. Полученные ПН разнятся в пределах допустимой погрешности.
3. Обсуждение
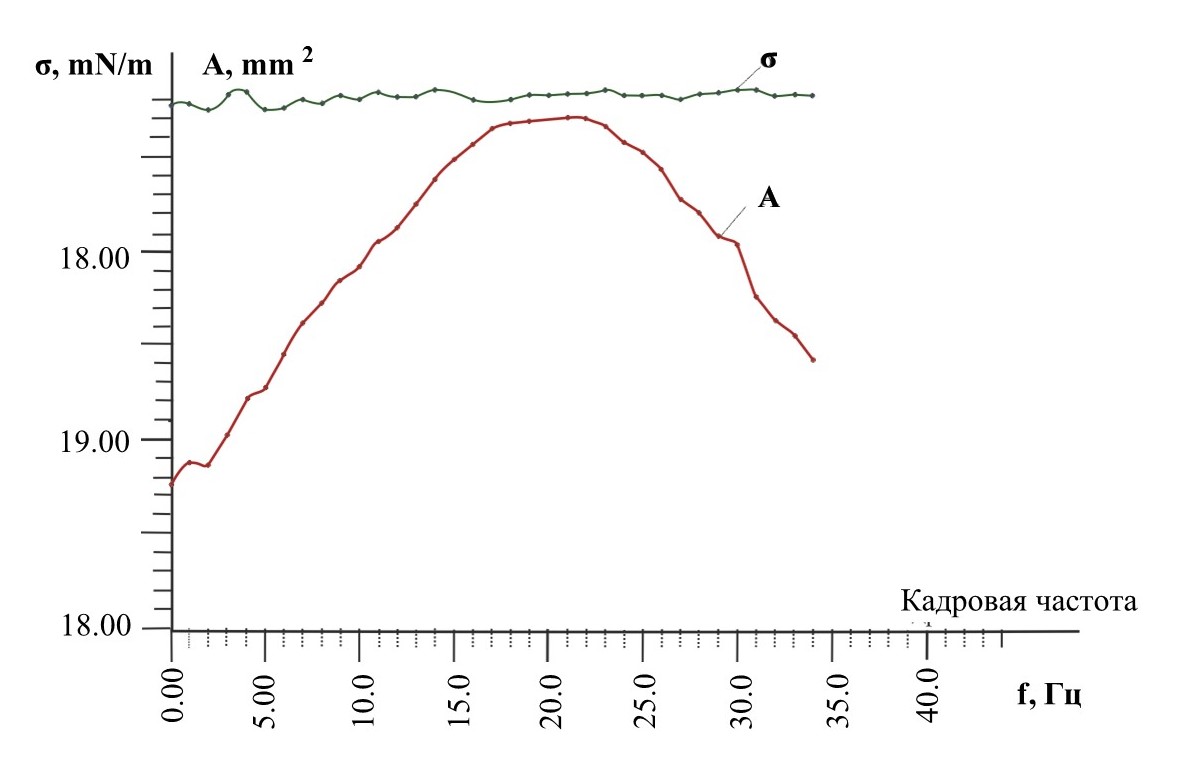
Рисунок 2 - Зависимость поверхностного натяжения и синусоидально изменяющегося объема висящей капли пропанола-2 от времени
Увеличение частоты осцилляции капли подразумевает увеличение скорости сдвига жидкости , .
Рисунок 3 (а) иллюстрирует периодичность ПН при изменении частоты и амплитуды объема капли (от 0,5 Гц до 1 Гц и от 0,050 ml до 0,55 ml). Это связано с тем, что при таких частотах осцилляции молекулы поверхностно-активного вещества (ПАВ), в данном случае пропанола-2, успевают переориентироваться и адаптироваться к изменяющимся условиям на поверхности капли.
На рисунке 3 (а) и 3 (б) показаны графики сравнения кривых площади поверхности, осциллирующей капли и динамики величины ПН в зависимости во времени t.
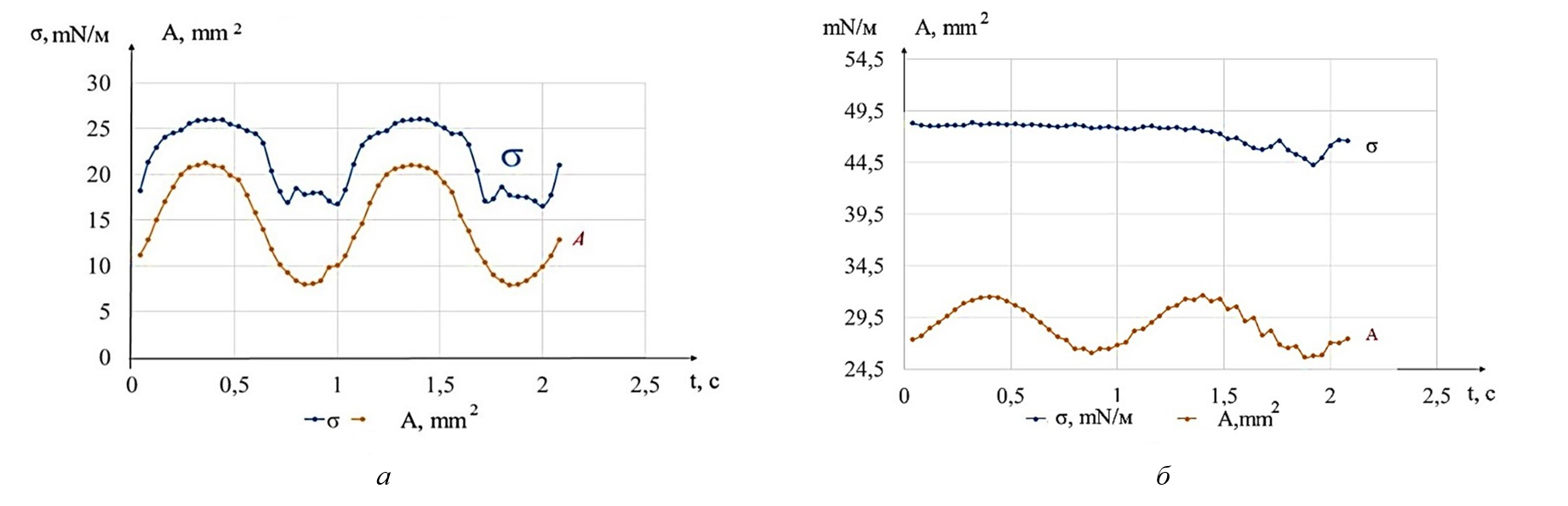
Рисунок 3 - Графики сравнения кривых поверхностного натяжения и площади, осциллирующей капли во времени на частоте 1 Гц:
а – для пропонола-2; б – для дистиллированной воды
Примечание: видеокамеры и осцилляции капли
Для получения явления периодичности в спиртосодержащем растворе на частоте колебания системы 0,5 Гц необходимо подобрать раствор соответствующей плотности.
Для реализации данной задачи были приготовлены спиртовые растворы хлорофилла (на основе пропанола-2). Полученный раствор хлорофилла имеет плотность 792,2 кг/м3, тогда как у пропанола-2 около 785,1 кг/м3, следовательно, можно утверждать, что при увеличении плотности системы была обнаружена периодическая зависимость ПН от времени (на частоте, висящей капли равной 0,5 Гц). Поскольку молекулы хлорофилла по размеру больше молекул одноатомного спирта (пропанола-2), то и время релаксации будут различаться. Данное утверждение согласуется с принципом Ле-Шателье-Брауна, согласно которому при отклонении физической системы от состояния устойчивого равновесия образуются силы, пытающиеся вернуть ее к равновесному состоянию , .
На рисунке 4 показаны усредненные графические модели кривых ПН и площади осциллирующей капли. Данный рисунок иллюстрирует одно полное колебание системы с фазовым сдвигом Δτ (параметр, зависящий от вязкости и эластичности пропанола-2) .
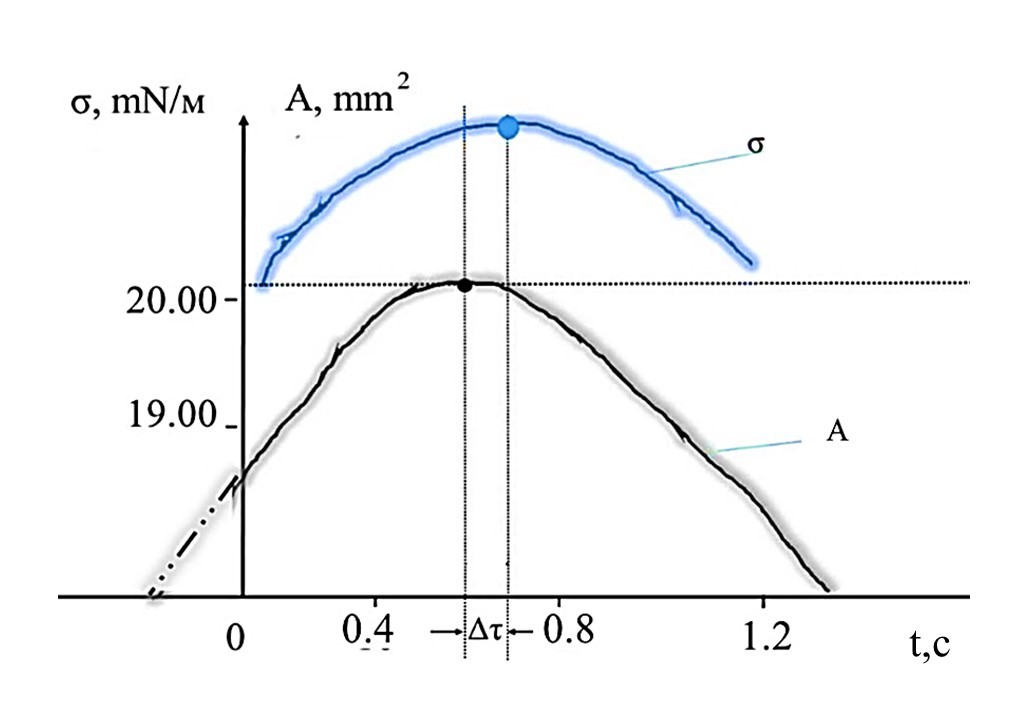
Рисунок 4 - График сравнения динамики поверхностного натяжения пропанола-2 и объема осциллирующей капли во времени
В системах, где использовались пропанол-2 или вода, наблюдалось отставание кривых ПН от объема осциллирующей капли. Так, на частоте равной 1 Гц кривая пропанола-2 относительно площади поверхности осциллирующей капли имеет фазовый сдвиг (∆τ). На частоте равной 2 Гц была зафиксирована периодичность ПН воды. На этой частоте осцилляции висящей капли воды (2 Гц с периодом равной 0,5 с) оптическая система просматривает форму капли 12,5 раз. Так как камера имеет частоту 25 кадров в 1 с. Тем не менее для оценки гистерезиса (отставание) кривой ПН воды частота камеры равная 12,5 изображений в секунду является достаточным условием.
Определение фазового сдвига между кривыми ПН и объемом осциллирующей капли (Рис. 3–7) сводится к решению пропорциональных зависимостей при разностях конечного fк и начального fн значений фазовых сдвигов между соседними кривыми (Δτ) в выделенном диапазоне времени. Как видно из рисунка 4, неравновесное ПН сдвинуто на величину ∆τ в течении которого система, выведенная из состояния равновесия релаксируются в соответствии с законом кинематической вязкости по формуле (1). Иными словами, фазовый сдвиг (определяемый по максимумам/минимумам кривых) есть отклонения системы от первоначального равновесного состояния, к которому она должна вернутся после снятия сдвигового напряжения.
Следующим этапом исследования является система вода – уксусная кислота – хитозан (ХТЗ).
Одним из ключевых факторов, влияющих на свойства раствора хитозана, является его концентрация и кислотная среда растворителя . В данном исследовании выбран подход, при котором последующий исследуемый раствор имеет концентрацию на 2,5% выше, чем предыдущий. Это позволяет оценить, как изменение концентрации влияет на гистерезис кривых ПН и площади осциллирующей капли.
Для получения раствора ХТЗ необходимо приготовить 2% раствор уксусной кислоты. Такой раствор был приготовлен путем смешивания уксусной кислоты и дистиллированной воды в определенных пропорциях.
Исследования проводились с использованием раствора ХТЗ в следующих концентрациях: 2,5%; 5%; 7,5%; 10%.
На рисунке 5 показаны кривые ПН и площади осциллирующей капли для полимера 2,5% ХТЗ. Временной (фазовый) сдвиг между кривыми ПН и площади осциллирующей капли, рассчитанных по максимумам синусоид составляет 0,04 с.
На рисунке 5 показаны зависимости кривых полимера 5% ХТЗ во времени. Фазовый сдвиг синусоид ПН и площади осциллирующей капли составляет 0,125 с.
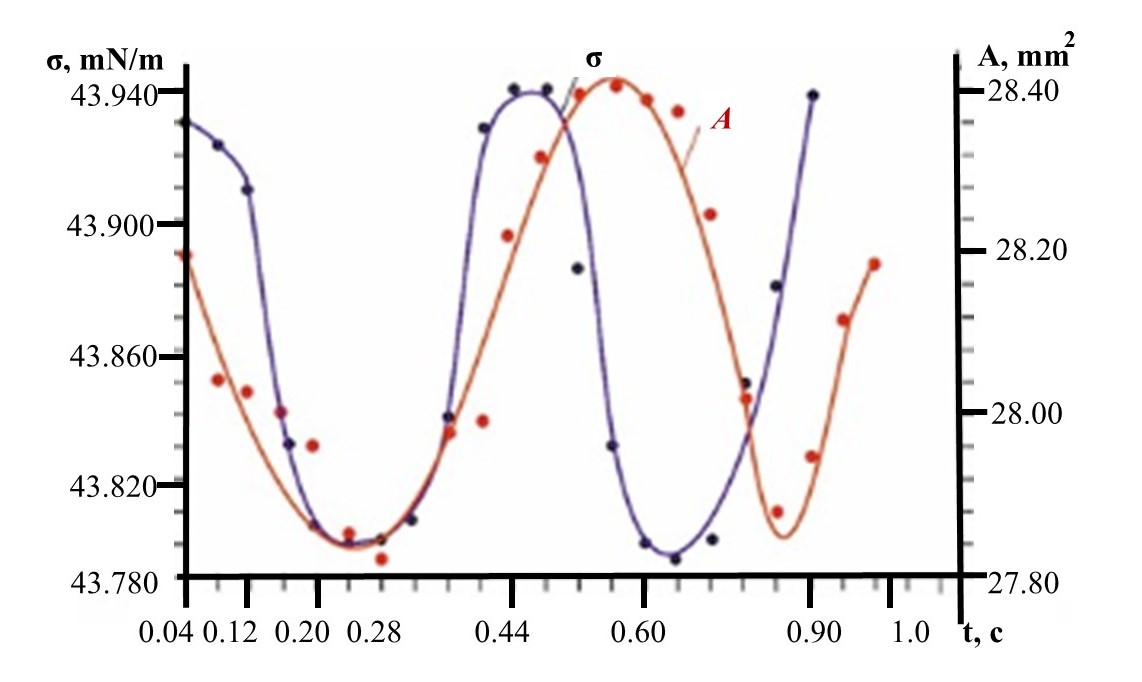
Рисунок 5 - Сравнение кривых площади (А), осциллирующей капли и поверхностного натяжения (σ) во времени (t)
Из рисунка 6 следует, что раствор ХТЗ при данной концентрации имеет фазовый сдвиг в пределах 0,22 с между кривыми синусоид ПН и площади осциллирующей капли.
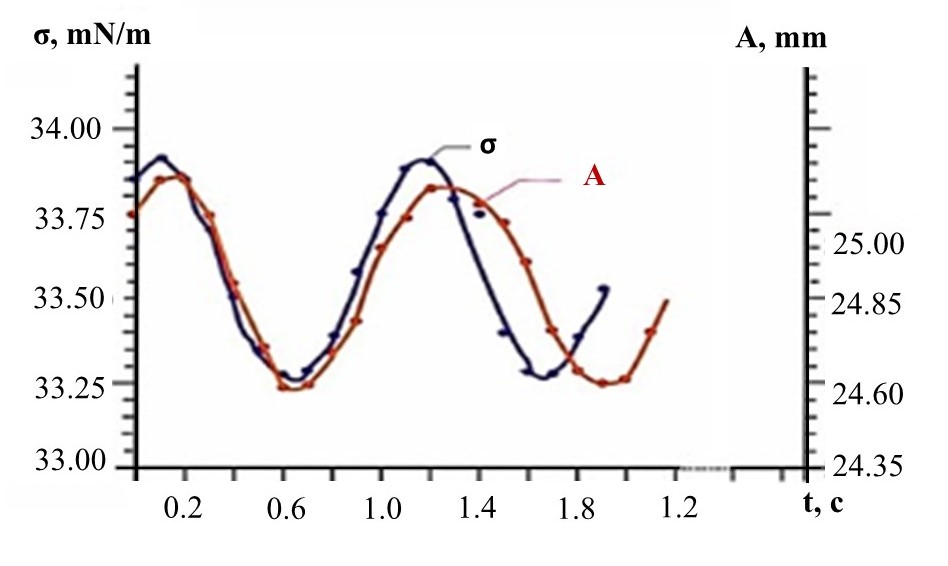
Рисунок 6 - Сравнение кривых площади (А), осциллирующей капли и величины поверхностного натяжения (σ) во времени (t)
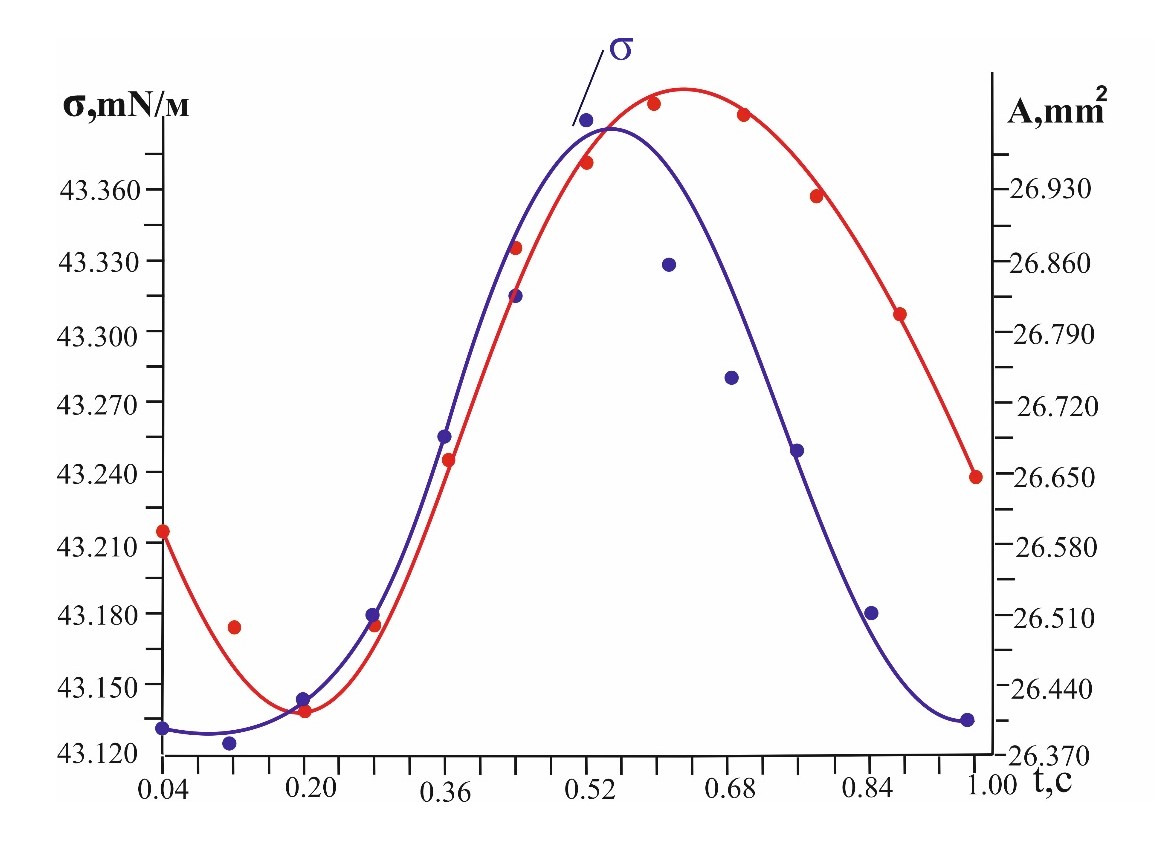
Рисунок 7 - Сравнение кривых площади (А), осциллирующей капли и величины поверхностного натяжения (σ) во времени (t)
4. Выводы
Последовательное исследование растворов хитозана в различных концентрациях продемонстрировало, что реологические кривые претерпевают временные сдвиги, амплитуда которых возрастает пропорционально плотности или концентрации раствора . Реологический анализ этих сдвигов между кривыми поверхностного натяжения и площади осциллирующей капли выявил порог динамической вязкости исследуемых растворов (например, раствора хлорофилла на основе пропанола-2). Экспериментальные данные отразили синусоидальную реологию дилатирующейся капли, фиксируя постепенный переход от постоянной вязкости пропанола-2 к динамической вязкости полимера хитозана. Дальнейший анализ концентрационной зависимости растворов хитозана выявил вязкоупругое сопротивление напряжениям сдвига. Представленная работа содержит информацию о процессах, протекающих на границе раздела фаз, и представляет научно-практический интерес, а также новизну в области дилатационной поверхностной реологии.
5. Заключение
1. Летучая жидкость (пропанол-2), использованная при проведении опытных работ, является маловязким растворителям, динамическая вязкость которой составляет 0,002038 Па∙с . ПН на всем протяжении колебательного процесса оставалась неизменной на частоте осцилляции висящей капли 0,5 Гц (Рис. 3). Добавление хлорофилла к пропанолу-2 позволило получить периодические колебания ПН на той же частоте (0,5 Гц). Также при увеличении частоты осцилляции площади поверхности капли до 1 Гц динамика ПН пропанола-2 демонстрирует периодическую зависимость.
2. Растворы ХТЗ различной концентрации позволили обнаружить параметры кинематической и динамической вязкости, характеризующие фазовые сдвиги. Растущие сдвиги между кривыми ПН и площади осциллирующей капли отмечались при концентрациях растворов ХТЗ от 2,5% до 7,5%. Дальнейшее увеличение концентрации ХТЗ (от 7,5% до 10%) показало сближение указанных кривых.
3. Проведенные исследования показали, что амплитуда колебания площади поверхности капли с увеличением концентрации растворов уменьшается из-за возросших модулей вязкости и эластичности.
4. Данный анализ полимера демонстрирует, что механизм изменений сдвигов реологических кривых подвержен в основном частоте осцилляции, висящей капли и плотности испытуемой жидкости. Исследованные факторы, такие как модуль эластичности и модуль вязкости подчеркивают сложность и многогранность временных сдвигов, формирующих представления о свойствах ХТЗ.
5. Оптимизация концентрации ХТЗ имеет решающее значение для достижения максимального эффекта. Сближение кривых при высоких концентрациях может свидетельствовать о формировании новой структуры, что приводит к изменению межмолекулярных взаимодействий и структурных переходов, влияющих на такие свойства, как вязкость, адгезия и биосовместимость. Понимание этих зависимостей позволит расширить сферу применения ХТЗ в медицине, фармацевтике, биотехнологиях и других областях.
