Influence of the observation interval on the accuracy of trend-based interval forecasting
Influence of the observation interval on the accuracy of trend-based interval forecasting
Abstract
This article is dedicated to the analysis of the influence of the length of the observation interval on the accuracy of interval forecasting and the search for ways to improve the forecasting technology in the direction of minimising the forecast error. It is noted that the level of research into the influence of the observation interval is insufficient for solving practical problems. The task of forecasting for the next year the number of cases in Russia of injuries, poisonings and some other consequences of external causes is reviewed. The obtained results show a significant, in some cases – multiple, influence of the length of the observation interval on the accuracy of interval forecasting. With a general tendency to decrease the forecast error estimate with the growth of the observation interval length, some periods of growth of the forecast error estimate can be observed. The author recommends conducting a series of trial forecasts with different observation intervals for interval forecasting and selecting the best one based on the forecast error estimation.
1. Введение
Прогнозирование краткосрочных и среднесрочных результатов развития социально-экономических, демографических и других связанных с жизнью общества процессов является важной составляющей информационного обеспечения процесса управления. Одним из инструментов прогнозирования служат трендовые модели. Трендовая модель – это инструмент, использующийся для анализа и прогнозирования временных рядов на основе выявления основной тенденции изменения какого-либо признака (тренда). Эти модели помогают определить, как переменные изменяются со временем, и позволяют делать прогнозы о будущих значениях на основе прошлых наблюдений.
Трендовые модели могут использоваться для получения как точечных, так и интервальных оценок прогноза.
Точечные оценки прогноза представляют собой однозначную величину, которою трендовая модель выдает на определенный момент времени. Например, если аппроксимируем региональное потребление электроэнергии линейной регрессией, то подставив в уравнение линейного тренда номер следующего за интервалом наблюдения месяца, получим точечную оценку расхода этого ресурса на следующий месяц – предположим, 6447 млн кВт*ч. Очевидно, что абсолютно точное совпадение точечной оценки прогноза с фактическим расходом ресурса в следующем месяце – событие маловероятное. Данное обстоятельство снижает доверие к прогнозу, а также ценность точечной оценки прогноза для подготовки управленческого решения.
Интервальные оценки прогноза представлены диапазоном значений, в котором с определенной вероятностью будет находиться истинное значение прогноза. Эти интервалы учитывают неопределенность прогноза и обеспечивают более полное представление о возможных изменениях. Например, интервал может составить 6447 ± 900 млн кВт*ч с доверительной вероятностью 95%. Это означает, что мы с 95% уверенностью ожидаем, что истинный расход ресурса в следующем месяце окажется в диапазоне от 5547 до 7347. Следует отметить, что разные трендовые модели могут давать близкие точечные оценки прогноза, при этом интервальные оценки прогноза могут существенно различаться. Например, квадратичная трендовая модель может иметь практически такую же точечную оценку – 6443. Однако оценка ошибки прогноза по этой модели может оказаться значительно меньше – 150, что приведет к более узкому доверительному интервалу: 6443 ± 150 млн кВт*ч с доверительной вероятностью 95% (от 6293 до 6593). Использование интервальных оценок позволяет более эффективно анализировать и интерпретировать данные, снижая риск принятия решений на основе недостаточно информативных прогнозов.
Практически во всех исследованиях, посвященных прогнозированию временных рядов, отмечается влияние интервала наблюдения на ошибку прогноза. Однако известные исследования не содержат оценок значимости этого влияния, а также не предоставляют четких рекомендаций по выбору интервала наблюдения для интервального прогнозирования, ограничиваясь общей рекомендацией: принимать длину периода прогнозирования, т.е. срока удаления прогнозируемого уровня во времени от конца базы расчета тренда не более трети, в крайнем случае, половины длительности интервала наблюдения , .
Также существует мнение, что ошибка статистического прогноза будет тем меньше, чем меньше срок упреждения (период прогнозирования) и чем длиннее информационная база прогноза (интервал наблюдения) . Из этого утверждения следует, что увеличение длины интервала наблюдения повышает точность прогноза. К сожалению, обоснования указанного утверждения в работе не приводится.
Для практического использования технологий прогнозирования важно оценить погрешность прогноза , а снижение погрешности прогноза улучшает качество информационного обеспечения процесса управления. Поэтому представляется достаточно актуальной задача совершенствования технологии прогнозирования в направлении минимизации ошибки прогноза, что будет содействовать минимизации риска принятия решений на основе недостаточно информативных прогнозов.
Исследование основывается на методах математической статистики, методах анализа и прогнозирования временных рядов, а также на статистических данных, размещенных на официальном сайте Федеральной службы государственной статистики, статистических материалах Департамента мониторинга, анализа, и стратегического развития здравоохранения Министерства здравоохранения.
2. Основные результаты
Одним из преимуществ применения методов математической статистики при анализе и прогнозировании временных рядов является возможность аналитической оценки неопределенности . Имеются аналитические зависимости для расчета оценки ошибки прогноза для линейной, квадратичной и кубической модели :
где ta – критическое значение t-статистики Стьюдента при уровне значимости α;
σ – среднеквадратическое отклонение расчета по модели и исходных данных;
n – длина интервала наблюдения;
k – отсчитываемый от середины интервала наблюдения номер элемента временного ряда, для которого составляется прогноз;
Σ t2, Σ t4 и Σ t6 – сумма возведенных соответственно во вторую, четвертую и шестую степень номеров элементов интервала наблюдения, отсчитываемых от его середины.
Длина интервала наблюдения n в явном виде входит в формулы расчета ошибок прогноза. Кроме того, большая часть входящих в формулы ошибок прогноза величин зависит от длины интервала наблюдения:
1. Критическое значение t-статистики Стьюдента при заданном уровне значимости α зависит только от числа степеней свободы, т.е. разности между длиной интервала наблюдения и количеством коэффициентов модели. Значение ta максимально при числе степеней свободы, равном единицы. С ростом числа степеней свободы значение ta снижается, что означает снижение ta с увеличением длины интервала наблюдения.
2. Отсчитываемый от середины интервала наблюдения номер элемента временного ряда k увеличивается на половину увеличения длины интервала наблюдения.
3. Суммы возведенных во вторую, четвертую и шестую степень номеров элементов интервала наблюдения, отсчитываемых от его середины, увеличиваются с увеличением длины интервала наблюдения.
Входящее в аналитические зависимости расчета оценки ошибки прогноза среднеквадратическое отклонение определяется по формуле:
где yi – расчет по модели для i-го интервала наблюдения;
y0i – фактическое значение прогнозируемого параметра для i-го интервала наблюдения.
На первый взгляд, поскольку длина интервала наблюдения находится в знаменателе формулы, то можно ожидать, что среднеквадратическое отклонение с увеличением длины интервала наблюдения будет уменьшаться. Однако среднеквадратическое отклонение зависит, прежде всего, от расхождения расчетных и фактических данных, на которое влияет множество факторов, включая сложность модели и качество самих данных. Поэтому увеличение длины интервала наблюдения в отдельных случаях может приводить к росту среднеквадратического отклонения (например, при включении в интервал наблюдения аномальных данных).
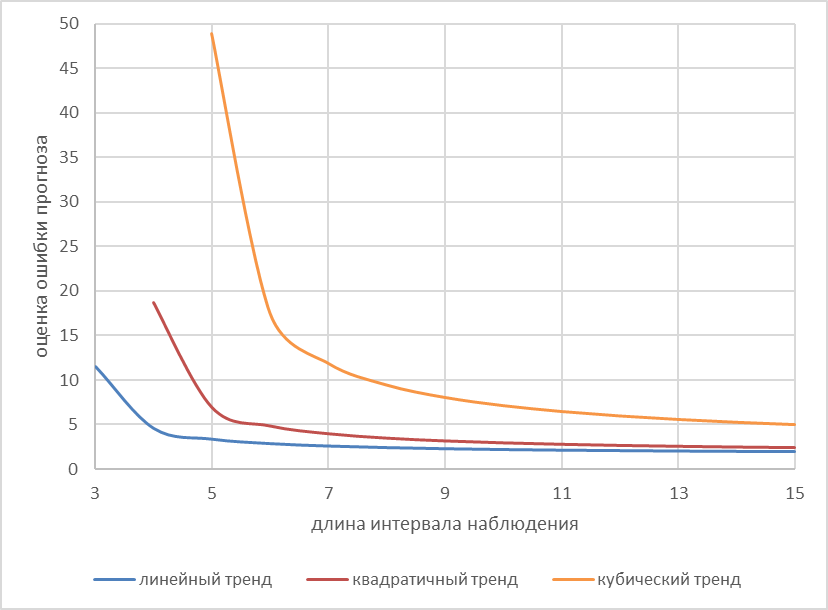
Рисунок 1 - Зависимость оценки ошибки прогноза от длины интервала наблюдения при σ = 1
При постоянном значении среднеквадратического отклонения увеличение длины интервала наблюдения действительно повышает точность прогноза – для всех видов тренда на рис. 1 наблюдается монотонное убывание оценки ошибки прогноза.
Минимальной длине интервала наблюдения соответствуют максимальные значения оценок ошибок прогноза, причем при увеличении длины интервала наблюдения на две единицы оценка ошибки снижается в 3-4 раза.
Для анализа значимости влияния интервала наблюдения на ошибку на точность интервального прогнозирования при переменном значении среднеквадратического отклонения рассмотрим задачу прогнозирования на следующий год количества случаев травм, отравлений и некоторых других последствий воздействия внешних причин (далее – количество травм). Сведения о количестве таких происшествий в России в 2000-2022 годах имеются в отчете «Заболеваемость населения по основным классам болезней» , размещенном на официальном сайте Федеральной службы государственной статистики. Данные за 2023 год приведены в статистических материалах Департамента мониторинга, анализа, и стратегического развития здравоохранения Министерства здравоохранения Российской Федерации . Исходные данные за последние 15 лет сведены в таблицу 1.
Таблица 1 - Исходные данные
Год | Количество травм на 1000 человек населения | Год | Количество травм на 1000 человек населения | Год | Количество травм на 1000 человек населения |
2009 | 90,0 | 2014 | 90,7 | 2019 | 89,7 |
2010 | 91,7 | 2015 | 90,1 | 2020 | 80,6 |
2011 | 92,7 | 2016 | 88,6 | 2021 | 82,8 |
2012 | 93,6 | 2017 | 87,7 | 2022 | 85,6 |
2013 | 92,4 | 2018 | 88,4 | 2023 | 87,2 |
На представленной на рис. 2 графической интерпретации исходных данных можно отметить:
- отсутствие явно выраженной тенденции (отмечается как рост, так и снижение количества травм, а также имеются локальные экстремумы – в 2012, 2017, 2019 и в 2020 годах меняется направление изменения данных);
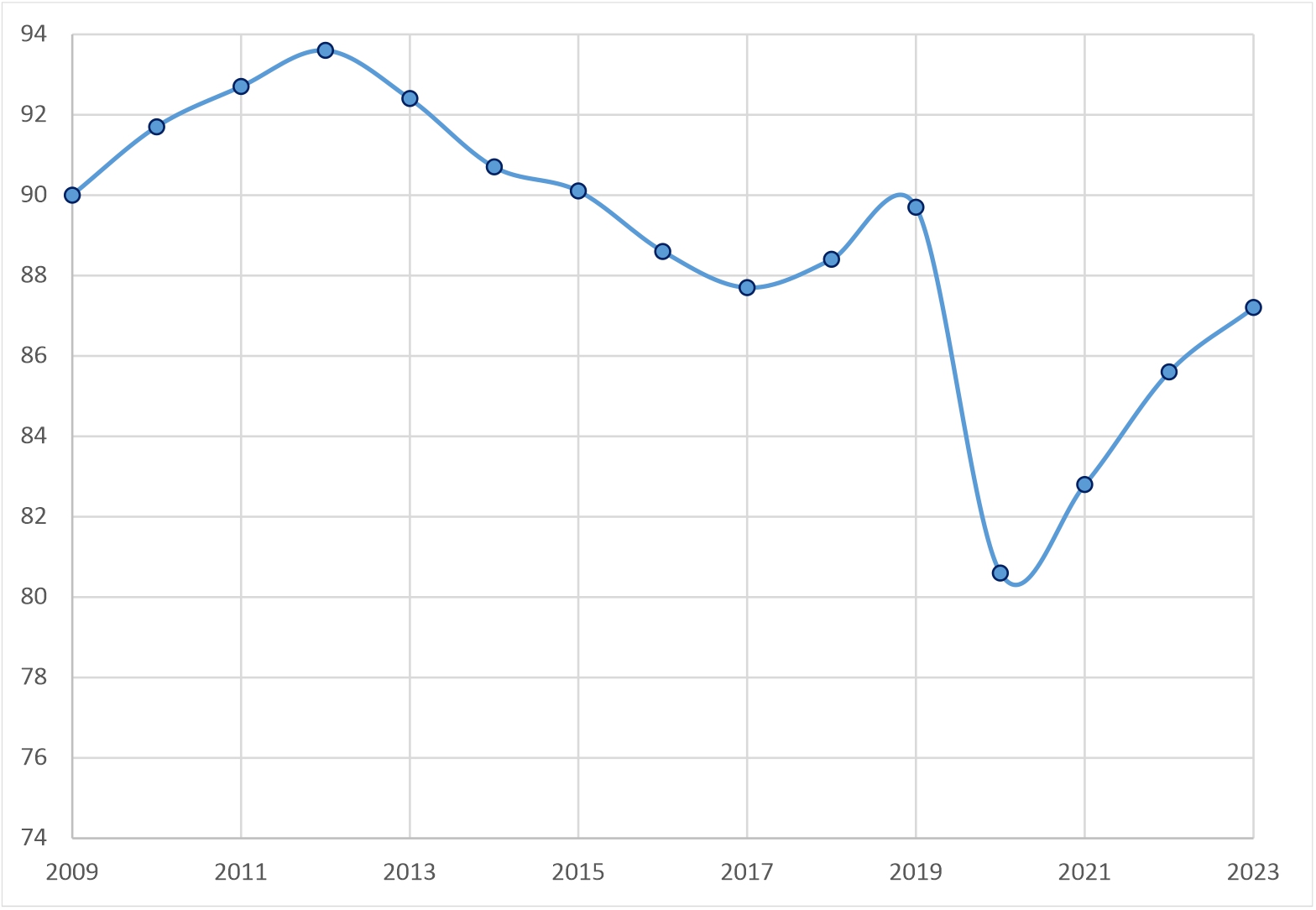
Рисунок 2 - Сведения о количестве травм
Что касается использования теоремы Котельникова для прогнозирования временного ряда, то стоит отметить несколько аспектов:
- теорема позволяет эффективно связывать частотные свойства временного ряда с его значениями во временной области и может использоваться в частотном анализе для предсказания будущих значений;
- теорема подразумевает определённые условия, такие как линейность и стационарность, которые не всегда выполняются в реальных данных временных рядов (в том числе и в данных рассматриваемой задачи);
- если временной ряд не стационарен или имеет сложную структуру, простое применение теоремы может оказаться неэффективным;
- методика интервального прогнозирования с использованием теоремы Котельникова в настоящее время недостаточно разработана.
С учетом изложенного теорема Котельникова не включена в математический аппарат данного исследования.
В список трендовых моделей для данного исследования в дополнение к линейному, квадратичному и кубическому тренду включим показательную модель, поскольку она линеаризуется при логарифмировании :
где х – номер года, отсчитываемый от начала интервала наблюдения.
Регрессионный анализ сводится к поиску значений коэффициентов модели, при которых достигается минимальная сумма квадратов отклонений между расчетом по модели и фактическими данными . Анализ проводился в программе Microsoft Excel (надстройка «Пакет анализа») с доверительной вероятностью 90% для интервалов наблюдения от 3 до 15 лет. В соответствии с принятой доверительной вероятностью из рассмотрения исключались модели с недостаточной статистической значимостью уравнения (значимостью критерия Фишера более 0,1), а также с недостаточной статистической значимостью коэффициентов уравнения (вероятностью справедливости гипотезы о равенстве коэффициента модели нулю более 0,1).
Для решаемой задачи квадратичная и кубическая модели оказались непригодны: варианты этих моделей практически для всех длин интервалов наблюдения пришлось исключить ввиду недостаточной статистической значимости уравнения модели или его коэффициентов. Единственная статистически значимая модель – кубический тренд для пятнадцатилетнего интервала наблюдения в два раза уступает по точности прогноза линейному тренду для той же длины интервала наблюдения.
Результаты расчетов оценок ошибок прогноза для линейного и показательного тренда приведены на рис.3.
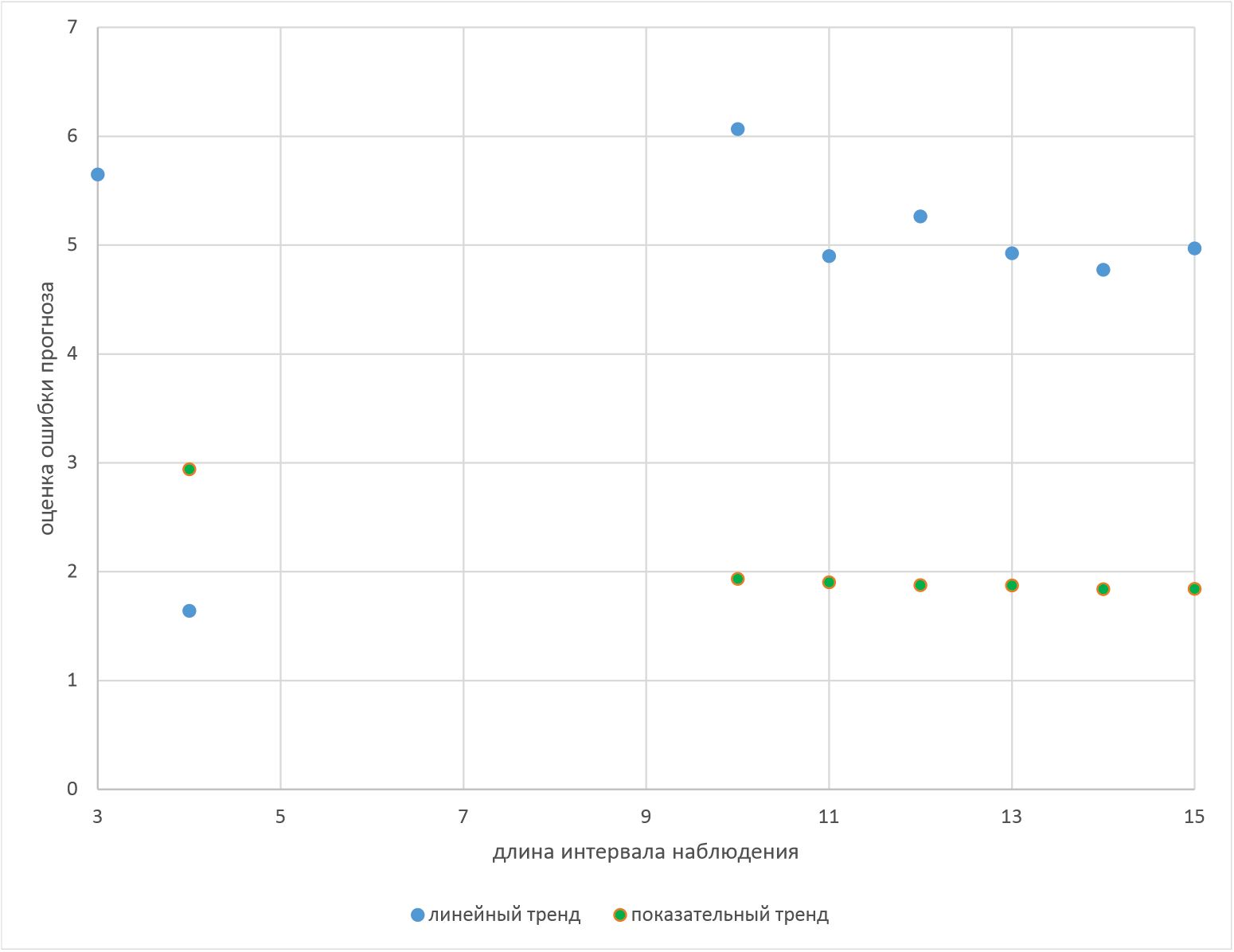
Рисунок 3 - Зависимость оценки ошибки прогноза от длины интервала наблюдения
Известно, что аномальные данные оказывают наибольшее влияние на результаты регрессионного анализа в том случае, когда они расположены в середине интервала данных. Действительно:
в интервалы наблюдения до 5 лет (с 2020 по 2023 год) аномальное изменение данных не входит и, соответственно, влияния результаты регрессионного анализа не оказывает;
в интервалах наблюдения от 5 до 9 лет влияние аномальных данных, накладываясь на влияние неустойчивой динамики изменения данных, существенно снижает статистическую значимость регрессионных моделей;
в интервалах интервалов наблюдения от 10 лет влияние аномальных данных пятого временного интервала снижается до уровня, позволявшего получить статистически значимые модели.
Варианты прогнозов для статистически значимых регрессионных моделей сведены в таблицу 2. Входящая в уравнение модели величина х – номер года, отсчитываемый от начала интервала наблюдения, поэтому для прогноза на один год х = n + 1.
Таблица 2 - Варианты прогнозов
№ п/п | Длина интервала наблюдения | Уравнение модели | Прогноз | Оценка ошибки прогноза |
1. | 3 года | y = 2,2 х + 80,8 | 89,6 | 5,65 |
2. | 4 года | y = 2,26 х + 78,4 | 89,7 | 1,64 |
3. | ln(y) = 0,0269 х + 4,364 | 89,86 | 2,94 | |
4. | 10 лет | y = –0,679 х + 90,87 | 83,41 | 6,06 |
5. | ln(y) = –0,00782 х + 4,51 | 83,42 | 1,93 | |
6. | 11 лет | y = –0,679 х + 90,87 | 83,41 | 6,06 |
7. | ln(y) = –0,00782 х + 4,51 | 83,42 | 1,93 | |
8. | 12 лет | y = –0,806 х + 93,35 | 82,88 | 5,26 |
9. | ln(y) = –0,00915 х + 4,54 | 82,96 | 1,88 | |
10. | 13 лет | y = –0,784 х + 93,96 | 82,98 | 4,93 |
11. | ln(y) = –0,00889 х + 4,54 | 83,06 | 1,87 | |
12. | 14 лет | y = –0,719 х + 94,1 | 83,3 | 4,77 |
13. | ln(y) = –0,00816 х + 4,55 | 83,36 | 1,84 | |
14. | 15 лет | y = –0,617 х + 93,72 | 83,85 | 4,97 |
15. | ln(y) = –0,00702 х + 4,54 | 83,87 | 1,84 | |
16. | y = 0,023 х3–0,58 х2+3,4 х+87,1 | 88,58 | 10,24 |
Оценки ошибок прогноза для показательного тренда в интервале наблюдения от 10 до 15 лет оказались ниже соответствующих оценок для линейного тренда. При этом минимальная оценка ошибки прогноза Δ = 1,64 получена для линейного тренда при длине интервала наблюдения четыре года.
Рассмотренный пример свидетельствует о существенном влиянии длины интервала наблюдения на точность интервального прогнозирования на основе тренда: максимальная оценка ошибки прогноза линейного тренда больше минимальной в 3,7 раза. Для показательного тренда максимальная ошибка больше минимальной в 1,6 раза. При этом уравнение этого тренда для интервала наблюдения в три года оказалось статистически незначимым, в противном случае соотношение максимальной и минимальной ошибок было бы выше.
При общей тенденции к уменьшению оценки ошибки прогноза при росте длины интервала наблюдения наблюдаются отдельные периоды роста оценки ошибки прогноза (так, на рис.2 отмечается рост оценки ошибки прогноза линейного тренда при переходе от четвертого года к десятому и от четырнадцатого к пятнадцатому).
Для прогнозирования выбираем модель с минимальным значением оценки ошибки прогноза – вариант линейного тренда, полученный для интервала наблюдения четыре года. Эта модель обеспечивает хорошее качество описания исходных данных – коэффициент детерминации R2 = 0,99, статистически значима на уровне значимости 0,005 (0,5%). Положенное в основу прогнозирования предположение о случайности ошибок аппроксимации подтверждено проверками:
- равенства нулю суммы ошибок аппроксимации (значение критерия Стьюдента меньше критического значения, 0 < 2,92);
- случайности колебаний ошибок аппроксимации по критерию «поворотных точек» ;
- соответствия распределения ошибок аппроксимации нормальному закону распределения на основе критерия Харке – Бера .
Точечную оценку прогноза получаем при подстановке в уравнение модели номера года x= 5 (номер года, следующего за интервалом наблюдения):
Интервальный прогноз:
Прогнозируем, что количество случаев травм, отравлений и некоторых других последствий воздействия внешних причин в России в 2024 году с вероятностью 90% окажется в пределах от 88,06 до 91,34 на 1000 человек населения.
Автор полагает, что эффект от изменения длины интервала наблюдения зависит от свойств временного ряда данных и выбранной трендовой модели.
3. Заключение
Выводы:
- полученные результаты о существенном, в некоторых случаях – кратном, влиянии длины интервала наблюдения на точность интервального прогнозирования;
- при общей тенденции к уменьшению оценки ошибки прогноза при росте длины интервала наблюдения могут наблюдаться отдельные периоды роста оценки ошибки прогноза;
- при интервальном прогнозировании целесообразно провести серию пробных прогнозов с различными интервалами наблюдения и выбрать наилучший на основе оценки ошибки прогноза.
