DEVELOPMENT OF MATHEMATICAL MODEL FOR OPTIMIZATION OF EVAPORATORS WITH INDUCTIVE HEATING OF LIQUEFIED HYDROCARBON GAS

В современной мировой практике энергоснабжения промышленных, коммунальных и сельскохозяйственных потребителей, удаленных от опорных пунктов газоэнергоснабжения все более широкое применение находят децентрализованные системы энергоснабжения потребителей с использованием пропан-бутановых смесей сжиженного углеводородного газа (СУГ)

Использование сжиженных углеводородных газов в качестве основного или резервного источника энергии предполагает, перед подачей потребителю, их перевод из жидкого состояния в газообразное, т.е. искусственное испарение в специальных устройствах – испарителях с жидкой и твердотельными теплопередающими средами, обладающих значительными материалоемкостями

Предлагаемая математическая модель оптимизации испарителя с индукционным нагревом сжиженного углеводородного газа

Математическое моделирование является одним из основных положений системного анализа (подхода), под которым подразумевается методология и организация выполнения научных исследований, обеспечивающая требуемую достоверность результатов, при обосновании и оптимизации теплоэнергетического оборудования.

Объектом анализа являются электрические промышленные испарители пропан-бутановых смесей сжиженных углеводородных газов.

Основными задачами исследований являются:

1) составление расчетной структурной схемы электрических промышленных испарителей СУГ;

2) разработка математической модели оптимизации электрических промышленных испарителей СУГ;

3) сравнение конкурирующих вариантов электрических промышленных испарителей СУГ.

Структурирование и определение внешних связей электрических промышленных испарителей относят к первоначальным положениям системного экономического анализа.

Структурирование основано на том, что объект исследований представляется целостной системой

В качестве сравниваемых приняты следующие варианты.

1. Вариант n=1 – промышленный трубный испаритель на базе электрического испарителя с жидкой промежуточной теплопередающей средой на основе диэтиленгликоля.

2. Вариант n=2 – промышленный трубный испаритель на базе электрического испарителя с твердотельной промежуточной теплопередающей средой из алюминия.

3. Вариант n=3 – промышленный трубный испаритель на базе электрического испарителя с индукционным нагревом сжиженного углеводородного газа.

Отобранные варианты имеют одинаковое количество элементов m.

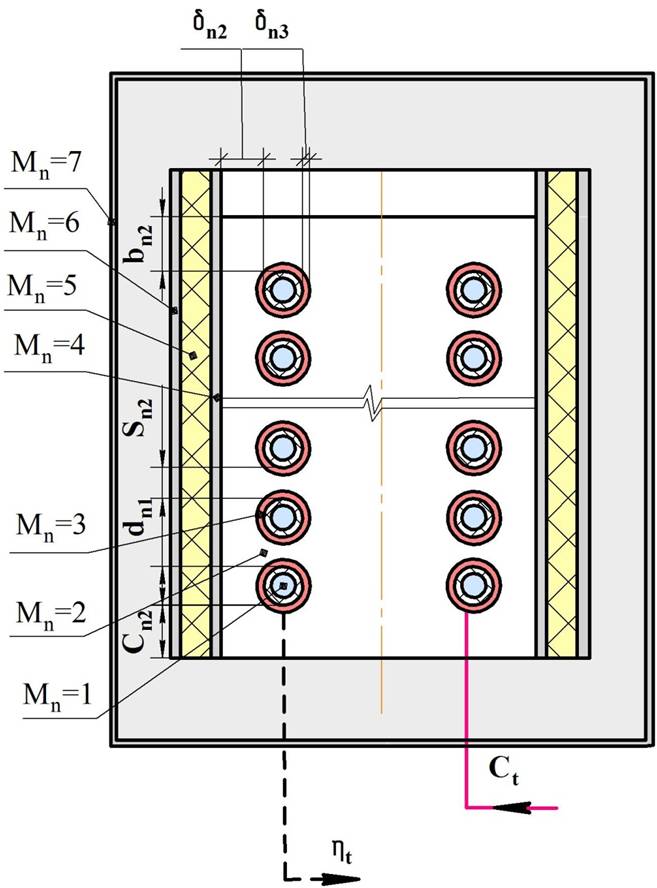
Рисунок 1 - Структурная схема n-го варианта промышленного трубного испарителя

DOI:10.23670/IRJ.2024.142.122.1

Где Mn=1 – змеевиковое испарительное устройство;

Mn=2 – внутреннее пространство n-го варианта промышленного трубного испарителя;

Mn=3 – электрический нагревательный элемент;

Mn=4 – корпус n-го варианта промышленного трубного испарителя;

Mn=5 – тепловая изоляция n-го варианта промышленного трубного испарителя;

Mn=6 – защитный футляр n-го варианта промышленного трубного испарителя;

Mn =7 – шкаф для защиты n-го варианта промышленного трубного испарителя от воздействия ветра, снега и дождевых осадков.

На структурной схеме показаны: сплошной линией – отпуск энергоносителя из внешней в собственную сеть энергоснабжения по цене Сt; пунктирной линией – обратная связь, характеризующая с помощью коэффициента полезного действия ηt, эффективность использования энергоносителя в n-м варианте промышленного трубного испарителя.

При математическом моделировании в качестве управляющего принимаются параметры, оказывающие противоположное влияние на капитальные вложения и эксплуатационные расходы, на оплату энергоресурсов. Проведенный анализ показывает, что управляющими параметрами являются величины:

- расстояния между соседними витками испарительного трубного змеевика n-го варианта трубного испарителя (ВТИ) Sn2, расстояния в свету между наружной стенкой испарительного трубного змеевика и корпусом n-го ВТИ δn2;

- расстояния между наружными поверхностями нагревательных элементов и испарительного змеевика n-го ВТИ δn3;

- расстояния между верхом испарительного змеевика и верхом корпуса n-го ВТИ bn2;

- расстояния между низом испарительного змеевика и низом корпуса n-го ВТИ Сn2, так как их влияние на основные и дополнительные капитальные вложения и эксплуатационные затраты в n-ый ВТИ в большинстве случаев противоположно друг другу.

Так, например, при увеличении Sn2, δn2, δn3, Сn2, bn2 значения материалоемкости промежуточных теплопередающих сред; нагревательных элементов; корпуса; теплоизоляции; кожуха для защиты теплоизоляции от увлажнения и повреждений; защитного шкафа, предотвращающего проникновение атмосферных осадков, n-го ВТИ и, соответственно, значения капитальных вложений в эти элементы также возрастают, а значения металлоемкости и капитальных вложений в испарительный змеевик уменьшаются и наоборот.

При возрастании значений параметров Sn2, δn2, δn3, Сn2, bn2 повышаются капитальные вложения и затраты на эксплуатацию, которые связанны с ремонтом n-го ВТИ.

С другой стороны, в этом случае, снижаются материалоемкость, капитальные вложения и затраты на эксплуатацию, которые связанны с ремонтом змеевикового испарительного устройства.

Предлагаемая математическая модель (1)-(6) получена для временного интервала t = 0, 1, 2 ... T и включает в себя:

- целевую функцию (1)-(4);

- структурную схему n-го варианта промышленного трубного испарителя СУГ, показанную на рисунке 1;

- систему ограничений управляющих параметров (5);

- уравнение теплового баланса (6).

Рассмотрим каждую из составляющих математической модели (1)- (6) более подробно.

1. Целевая функция. В качестве критерия оптимальности целевой функции, согласно

(1)

(2)

где t – расчетный год эксплуатации n-го в ВТИ;

Т – срок службы n-го ВТИ, лет; принимается равным сроку службы системы энергоснабжения Тсл =25 лет;

Ct – удельная стоимость энергии в пункте отпуска энергоносителя промышленному объекту, руб./МВт·ч;

Qпn. – общее годовое потребление энергоносителя, полезно используемого n-м ВТИ, МВт;

τ – число часов работы n-го ВТИ в течение года, ч;

ηt – коэффициент полезного действия n-го ВТИ, д.е;

f – количество замен m-го элемента в течение срока службы n-го ВТИ, f = Т/tm ;

tm – срок службы m-го элемента n-го ВТИ, год;

Е – норма дисконта, 1/год; принимается равной 0,12, то есть средней кредитной ставке банка;

Кn.m, Kn.m.доп – соответственно, основные и дополнительные капвложения в изготовление m-го элемента n-го ВТИ, руб.;

Иin – i-й вид эксплуатационных затрат n-го ВТИ, руб./год;

Sn2 - расстояние между соседними витками испарительного трубного змеевика n-го ВТИ, м.; 

δn2 – расстояние в свету между наружной стенкой испарительного трубного змеевика и корпусом n-го ВТИ, м.;

δn3 - расстояние между наружными поверхностями нагревательных элементов и испарительного змеевика n-го ВТИ, м.;

bn2 – расстояние между верхом испарительного змеевика и верхом корпуса n-го ВТИ, м.;

Сn2 – расстояние между низом испарительного змеевика и низом корпуса n-го ВТИ, м.

Дополнительные капитальные вложения в m-й элемент монтажа для каждого n-го ВТИ, связанные с установкой промышленного трубного испарителя на фундамент, обвязкой трубопроводами, электрокоммуникациями, испытанием и сдачей в эксплуатацию, определяются как доля отчислений от основных капиталовложений Knm на монтаж n-го ВТИ по формуле:

(3)

где n.э – доля годовых отчислений от Kn.m. и Kn.m.доп на эксплуатацию m-го элемента n-го ВТИ, д.е.

Расходы по эксплуатации  для каждого n-го ВТИ, связанные с капитальным (m=1), текущим (m=2) ремонтом и обслуживанием (m=3), определяются как доля годовых отчислений на эксплуатацию от Kn.m. и Kn.m.доп для n-го ВТИ по формуле:

(4)

где n.э – доля годовых отчислений от Kn.m. и Kn.m.доп на эксплуатацию m-го элемента n-го ВТИ, д.е.

Оценка стоимости энергоносителей при реализации математической модели осуществлялась в рублях по курсу 2023 года, без учета инфляционной составляющей.

2. Система ограничений управляющих параметров математической модели (1) - (6):

(5)

Величины  в формулах (1) - (6) являются независимыми (управляющими) параметрами, поскольку оказывают противоположное влияние на различные элементы основных и дополнительных капвложений Кn.m., Kn.m.доп и эксплуатационных затрат Иi.n при значениях m = 1;2;3. Так, при увеличении  значения капвложений Кn.2 – Кn.6 также увеличиваются, а значения Кn.1 уменьшаются и наоборот.

3. Уравнение теплового баланса предлагаемой математической модели, согласно результатам исследований

(6)

где p =1; 2; 3; 4 – соответственно, расслоенный, волновой, кольцевой и туманообразный режимы течения;

kp – коэффициент теплопередачи от теплопередающего элемента к СУГ, соответственно на участках с p =1; 2; 3; 4, Вт/(м2×К);

tт – температура теплопередающего элемента, оС;

d– наружный диаметр проточного испарительного трубопровода, м;

Fp –расчетная поверхность испарительного трубопровода СУГ, соответственно на участках с p =1; 2; 3; 4, м2;

Х n.н, Хn.гр – начальные и граничные значения степени сухости парожидкостной смеси пропан-бутан, соответственно на участках с p =1; 2; 3; 4

 – общий расход парожидкостной смеси СУГ, кг/ч;

rp.г.ср, сp.г.ср – средние значения скрытой теплоты парообразования и теплоемкости пропан-бутановой смеси, в интервалах ее выкипания, соответственно на участках с p =1; 2; 3; 4, определяемых в кДж/кг, согласно

tp.g.n, t p.g.k, – начальная и конечная температуры кипящей парожидкостной смеси пропан-бутан СУГ, соответственно на участках с p =1; 2; 3; 4, 0С.

1. В качестве управляющих параметров математической модели приняты величины: расстояния между соседними витками испарительного трубного змеевика Sn2, расстояния в свету между наружной стенкой испарительного трубного змеевика и корпусом испарителя δn2, расстояния между наружными поверхностями нагревательных элементов и испарительного змеевика испарителя δn3, расстояния между верхом испарительного змеевика и верхом корпуса испарителя bn2; расстояния между низом испарительного змеевика и низом корпуса испарителя Сn2, так как их влияние на основные и дополнительные капитальные вложения и эксплуатационные затраты в n-ый вариант промышленного трубного испарителя в большинстве случаев противоположно друг другу. 

2. Предлагаемая математическая модель (1)-(6) включает в себя:

– целевую функцию (1)-(4);

– структурную схему n-го варианта промышленного трубного испарителя (см. рисунок 1); 

– систему ограничений управляющих параметров (5);

– уравнение теплового баланса (6) и реализует высокий уровень сопоставимости конкурирующих вариантов.

Математическая модель оптимизации промышленных трубных испарителей сжиженного углеводородного газа (1)-(6) позволяет повысить достоверность расчетов, за счет учета динамики стоимости энергоресурса и ценовых факторов, таких как капитальные вложения и эксплуатационные затраты, в зависимости от ряда управляющих геометрических параметров: Sn2, δn2, δn3, Сn2, bn2.