ELEMENTARY QUARTIC FUNCTIONS AND SETS THEY FORM
Кокотов Ю.А.
Доктор химических наук,
Санкт-Петербург, Россия
ЭЛЕМЕНТАРНЫЕ КВАРТОВЫЕ ФУНКЦИИ И ОБРАЗУЕМЫЕ ИМИ МНОЖЕСТВА
Аннотация
Впервые замечено, что функциональный ряд разложения экспоненты разбивается на четыре ряда, определяющие элементарные квартовые функции: А(x) и С(x) (четные), В(x) и D(x) (нечетные) c простыми взаимосвязями между производными. Этими элементами образуются многие известные и неизвестные функции (непериодические, периодические, и «кентавры», состоящие из периодической и непериодической ветвей), составляющие квартовое множество. Квартовая формула описывает «состав» функций, модификация которого направленно изменяет их свойства, легко выявляемые численным моделированием. Сопоставление элементов А(x) и С(x), также как В(x) и D(x), выявляет необычное бесконечнократное пересечение их ветвей (не имеющих перегибов), соотносящееся с периодами происходящих от них тригонометрических функций.
Четыре мнимые квартовые функции вещественного аргумента (вместе с вещественными) образуют кроме обычных «тригонометрических» комплексных функций, также и функции с другим квартовым составом. Все они совместно образуют квартовое множество мнимых и комплексных функций. Введение четырех квартовых функций мнимого аргумента позволяет устанавливать и объяснять связи между функциями вещественного и комплексного квартовых множеств. Квартовый состав определяет общность многих внешне не связанных друг с другом, но образованных из квартовых элементов функций. Все это предоставляет широкие возможности практического применения самих квартовых функций в математике и физике.
Ключевые слова: квартовые: элементы, формула, функции (периодические, непериодические, кентавры, мнимые, мнимого аргумента), бесконечнократное пересечение, вещественное и комплексное квартовые множества.
Kokotov Yu.A.
PhD in Chemistry,
Saint-Petersburg, Russia
ELEMENTARY QUARTIC FUNCTIONS AND SETS THEY FORM
Abstract
We noted that exponential decomposition in series is divided into four series, which determine the elementary quartic functions: A (x) and C (x) (even), B (x) and D (x) (odd). Each of them can be considered as the 1st, 2nd or 3rd derivative of one of the others and as its own 4th derivative. These elements form real set of quartic functions (periodic, non-periodic and centauros, consisting of periodic and non-periodic parts). A comparison of the curves of the functions A(x) and C(x), B(x), and D(x) reveals an unusual phenomenon of their infinite mutual intersection (in the absence of inflections), conjugated with the periodicity of trigonometric functions. The four imaginary quartic elements are introduced in accordance with four real. Together they form a set of quartic complex functions, including not only ordinary ("trigonometric or Euler"), but also functions with other quartic composition. The introduction of four quartic elements of an imaginary argument easily explains the known and unknown connections between functions of real and of imaginary argument . The modification of the "quartic composition" of non-periodic and periodic functions of the quartic set, including usual, allow change their properties broadly and directionally. Numerical modeling reveals the most important and often unexpected features of functions related to a quartic set. Obviously, all of this explains the wide possibilities of applying quartic functions themselves in the field of theory and practice.
Keywords: quartic elements, formula, functions (periodical, non-periodical, сentaurus, imaginary, complex, imaginary argument), infinite multiple intersections, real and complex sets.
Statement of problem
A carefully study of the expansions in a series of exponents and some algebraic and trigonometric functions shows that they are formed by combinations of the four independent "sub series." The work is devoted to the analysis of non-obvious consequences of this obvious fact.
Results
A complete infinite power-factorial functional series of the exponent
![]() (1)
(1)
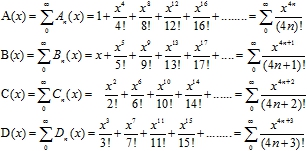
They define four independent quartic function A(x), B(x), C(x) and D(x)[1], which can be presented graphically (Fig. 1 ) .The quartic functions can be considered really both algebraic and geometric "elements" or elementary functions.
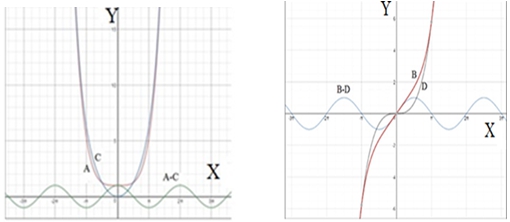
Fig. 1 – Quartic functions A(x) and С(х), B(x) and D(x) and their differences
Graphs of even functions A and C are two different U-shaped curves with a minimum and with infinitely increasing branches. They are located above the X-axis and are symmetrical with respect to the Y-axis. The coordinates of the minimum points, respectively, are (0,0) and (0,1). All members of their series, except for the first term of series A, are also even U-shaped functions
The curves of the odd quartic functions B and D are two different centrally symmetric S-shaped curves with one inflection in a neighborhood of zero. All members of their series, except for the first term of series B, are also odd S-shaped functions. Relationships between quartic functions and their derivatives and between the derivatives themselves are described by the table1.
Table 1 – The relationships between quartic functions and their derivatives
| F(x) | F(1)(x) | F(2)(x) | F(3)(x) | F(4)(x) | F(5)(x) | F(6)(x) | F(7)(x) | F(8)(x) |
| A | D | C | B | A | D | C | B | A… |
| B | A | D | C | B | A | D | C | B… |
| C | B | A | D | C | B | A | D | C… |
| D | C | B | A | D | C | B | A | D… |
They should be compared with the well-known relations of relevant algebraic and trigonometric functions.
The following known functions are determined by quartic functions, defined not only through series, but also in other way
1) Non periodic hyperbolic functions formed by the sums of two quartic series:
![]() (3)
(3)
2) Periodic trigonometric functions cosine and sine, formed by the differences of two quartic series:
![]() (4)
(4)
3) The proper exponent, determined by the sum of all four quartic series:
![]() (5)
(5)
4) The second exponent, determined by the differences of the same series:
![]() (6)
(6)
5) Four quartic series determined also two trigonometric functions (trigonometric binomials) that are less used and have no special names and designations:
They should be regarded as independent and important periodic functions.
In essence, all these are formulas of analytic geometry, establishing more complex than usual connections between algebra and geometry.
It follows from equations (3) - (4)) that the quartic functions themselves can be described by combinations of functions that have independent definitions also:
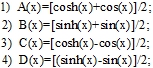 (9)
(9)
These formulas are certain "inverse" relations that determine algebraic functions through geometry and trigonometry.
Quite unusual and interesting are the centaurs - eight quartic functions, formed by the sums and differences of the series, originating from even and odd functions: ApB, AmB, ApD, AmD, BpC, BmC, CpD, CmD. Centaurs can also be defined and not analytically -by the functions exp(x), exp(-x), cps(x) and cms(x).
Their unusual graphs (Fig. 2) consist of three parts: a smooth part of exponential type infinitely extended along Y-axis ( to up or to down) and an "wave" parts infinitely extended along of the X-axis(to right or to left). Naturally, there is a relatively short transition part between these sections.
Centaurs turn out to be half sums of one of two non-periodic exponentials and one of two periodic trigonometric binomials. In the region of a slow increase in the exponential, the properties of the periodic component strongly prevail, and its wave part becomes practically periodic. In the region of rapid increase of the exponent, the traces of periodicity disappear, and its main part becomes practically exponential. The generality of non-periodic (both exponentials) and periodic functions is manifested in a completely unexpected way through "centaurs". Indeed, according to equation (5), (6). The exponents are decomposed not only into hyperbolic functions, but also to "centaurs". In general, the whole a subset of 14 sums and differences of two quartic functions can be considered as of quartic binomials, including 4 well-known and 10 other unknown functions.
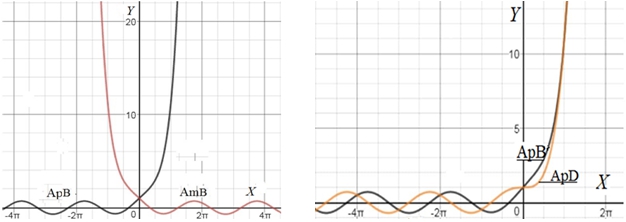
Fig. 2 – Three variants of centaur functions and their comparison
The eight functions determined by Eq. (7) - (10) and the functions: can be referred to as sub set of quartic four-element quadrinomials. Comparing quadrinomials , we notice that they form four pairs of functions of different types conjugated to each other. 1) Two well- known exponents are non-periodic functions. 2) Two periodic trigonometric binomials (Fig.3)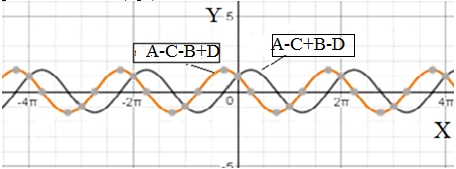
Fig. 3 – Trigonometric binomials cos(x)+sin(x) and cos(x)-sin(x)
3) Two (U) -shaped functions expressed in terms of the sum and difference of the hyperbolic cosine and the trigonometric sine (Fig.4).
4) Two S-shaped functions expressed in terms of the sum and difference of the hyperbolic sine and trigonometric cosine (Fig. 4).
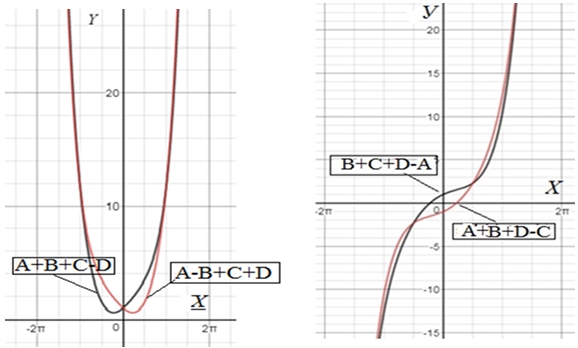
Fig. 4 – Two variants of U-shaped and two variants of S-shaped quadrinomials
Thus we find the existence, along with the exponents, of three important kinds of functions of common origin, having completely different characteristic properties.
It can be noted that among the functions considered above there are no sums and differences of exponentials and trigonometric sines and cosines. Such functions must to be "centaurs". The formulas of these centaurs should be attributed to three-element quadruples.
The quartic trinomials also include the set of non-trivial functions. For brevity, we will not consider this triples here, since there are too many of them. All graphics of them are variants of U-shaped or S-shaped forms. On some of the curves, two extrema (maximum and minimum) are formed in a neighborhood of zero.
The "quartic formulae" have been considered as the combination of the single symbols of certain "elements" (two element binomials, three element trinomials and four element quadruples ) up to now.
However, all functions originating from quartic series, including trigonometric, hyperbolic and exponents, can be modified, for example, by introducing into the formula of the quartic composition of integer or fractional coefficients
The quartic products and quotients (straight or cross) can be considered also. They contain analogs of conventional and hyperbolic tangent and cotangent (Figu5)
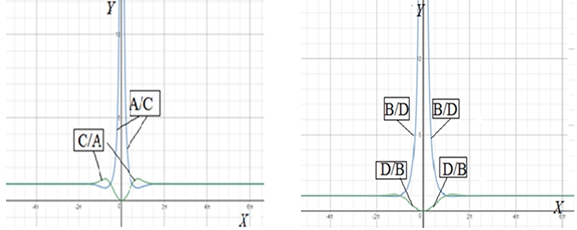
Fig. 5 – Four variants of quartic quotients
Various variants of quotients and products formed by quartic functions form curves that often have unexpectedly "quiet" and convenient properties. Recording and modification of various "quartic formulas" allows you to create a variety of quartic functions, change their properties in the desired direction, enhance or weaken their character properties. All these very different algebraic functions and their various geometric forms occur only from four U-shaped and S-shaped quartic "elements" and together form a common quartic set. All of them are formed by an exceptionally thin balance of factorial-power functions of the form: ![]()
Comparison of the quartic functions themselves reveals an unusual phenomenon of an infinite-multiple intersection of smooth curves, not related to the presence of any inflections on them.
The curves A and C, plotted on a common plot, intersect an infinite number of times, forming first explicitly, and then weakly expressed, stretched loops outwardly merging into one line. It is surprising that at the same time their intersecting branches do not have inflections. Both these curves intersect the smooth curve of the averaging function (ApC) / 2 at the same points, but in different directions.
The sum of both even functions ApC, is non-periodic hyperbolic cosine.
Their difference, AmC , is periodic cosine, having an infinite set of inflection points. To each cosine period corresponds one of the loops of the joint graph of two quartic curves. The point of inflection of the cosine curve corresponds to the point of intersection of the quartic curves.
The curves of the functions B(x) and D(x) on the joint graph intersect an infinite number of times (also in the absence of inflections), forming increasingly tapering and lengthening loops. Both these curves intersect the smooth curve of the averaging function (BpD)/2. The sums of both functions, BpD is a hyperbolic sine with one inflection in a neighborhood of zero. The curve of their difference, BmD, is a sinusoid. The completely unusual infinite-multiple intersection of quartic functions (in the absence of inflections) and the periodicity of trigonometric functions turn out to be interrelated phenomena.
The concept of quartic functions can be extended to imaginary and complex numbers. In this way, we can introduce four imaginary quartic functions of a real argument, which together with real form a quartic set of complex functions.
The usual ("trigonometric") complex functions ("numbers")
![]() (12)
(12)
These «trigonometric» complex functions and the complex Euler exponent are organically related precisely to such complex combinations of quartic functions, that enter in equations (16). Moreover, these combinations themselves can be considered as independent complex functions. However, other quartс combinations form completely different complex functions, for example, «hyperbolic»:
![]() (14)
(14)
They allow us to establish connections between various quartic functions of real and complex quartic sets and easily explain many unusual facts in the field of "complex numbers", for example, the well-known connections of certain real functions with the functions of an imaginary argument.
Graphic calculators provide ample opportunities for mathematical modeling of the functions considered, leading to often unexpected and useful results. Calculator «Desmos» well counts finite series of power -factorial type in a wide range of values of the argument, which allows us to consider "finite" models of real quartic functions. Experiments with models with a different number of terms (including those with a small number) reveal common tendencies of infinite series. With the help of finite models of quartic functions and their directional modifications, one can trace the formation and transformation of various non-periodic and periodic geometric curves, the formation of periodicity and waves, to demonstrate various wave phenomena. Simulation reveals an unusual multiple intersection of the curves of quartic functions and its relation to periodicity. The calculator finds the intersection points of the curves, establish their coordinates (as well as the coordinates of any points of the curves), consider the relative position of the curves of the functions being compared in the neighborhood of these points.
With the help of simple transformations, it is possible to change the relative position of the curves of the functions being compared on a joint graph. The relative displacement of the curves of the functions A(x) and C (x) along the ordinate axis changes the length of the loops, then simultaneously switches all the intersections into contact, eliminating the loops, and furthermore simultaneously and completely separates the function curves from each other. However, the periodicity of the corresponding difference functions is preserved, their curves simply shift up or down in the graph with respect to the abscissa axis without changing the shape. Even a small relative displacement of the compared curves along the abscissa axis sharply reduces the number of intersections and the size of the loops, violating the periodicity. Similar picture is observed with a vertical relative displacement of the functions B(x) and D(x), along the ordinate axis (the simultaneous transition of all intersections into contact, and then the disappearance of all contact at once). The sinusoid also moves vertically. With a relative displacement of the curves along the abscissa axis, the number of intersections of the functions decreases until they disappear completely. Naturally, with this, the periodicity also gradually disappears. Extremely interesting are the experiments on the modification of the quartic series themselves. For example, the functions
are respectively non periodic U and S-functions (Fig. 10). It means complete disappearance of the previously considered intersections elementary quartic functions due to the removal of the minor term of one of the quartic series.
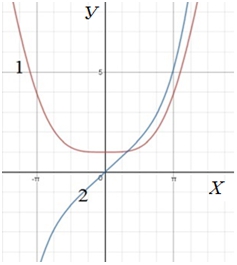
Fig. 7 – Disappearance of the periodicity of trigonometric functions due to the simple modification of one of the quartic series (eq.16)
The finite models of centaur functions demonstrate two smooth section: the "head" and the "tail". For centaurs with an infinite number of terms, the question of the second smooth section ("head" or "tail") becomes meaningless. The experiments also indicate that the wave part of the centaur outside the short transition region becomes a periodic function. Various variants of modification experiments with periodic and non-periodic functions, and with centauros allow one to trace the transition from non-periodic to periodic functions, and to observe the formation of waves on initially non-periodic functions. In general, the modification of the quartic composition of any of the functions (considered and not considered) creates wide possibilities for obtaining a multitude of curves of very different shapes. Quartic functions with various quartic formulas can be useful for describing and modeling periodic and wave processes, approximation and mathematical description of experimental data. They can be useful in solving various mathematical and physical problems. The next step is to extend the views considered here to 3D space using 3D calculators.
This paper demonstrates the continuing possibility of obtaining unexpected and useful results with respect to simple and well-known mathematical tools, considered in textbooks of the general mathematical plan (for example, [1]). It is not known what the mathematicians of the past knew from what was said here. They did not have a computer, let alone a graphic calculator.
Conclusions
The division of the exponential series into quartic series leads to the definition of four essentially different real quartic functions: A (x), B (x), C (x) and D (x). Their comparison reveals an unusual phenomenon of an infinite intersection of two curves, not connected with the existence of inflections on them.
The quartic functions can be considered and used as elements of quartic set, the various combinations of which form a variety of various and convenient quartic functions.
Specifically examined and compared are quartic binomials, trinomials, and quadruples that form a number of known and unknown functions (periodic, non-periodic, and "centaurs" that combine both kinds of functions). Quartic products and ratios or should be added to them.
In particular, quartic four members form four pairs of different functions, only one of which forms well-known and frequently used exponents.
The introduction of imaginary quartic functions of a real argument and quartic functions of an imaginary argument allows us to use them in the field of mathematics of "complex numbers". In particular, it is shown that in addition to the "trigonometric" complex functions, with which the complex Euler exponent is directly related, there are other types of complex functions (for example, hyperbolic).
The quartic functions allow us to clearly define the generality of a number of functions used in different sections of mathematics, sometimes felt earlier.
Interesting and important quartic functions in themselves and their various modifications can be useful for describing and modeling periodic and wave processes, approximation and mathematical description of experimental data. We can assume that they will be useful in solving many mathematical and physical problems.
[1]Further, to describe combinations of quartic functions, we introduce a number of easily understood notations in which the symbols are replaced by the symbols p, m and pm.
Список литературы / References
1.Fihtengolz G.M. Course of differential and integer calculus. Volume 1-3. – Saint-Peterbourg, 1997.