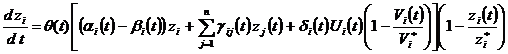ON THE ISSUE OF MATHEMATICAL MODELING MOTIVATION IN THE STUDY OF DIFFERENT PROCESSES
Харитонова Л.П.
Кандидат технических наук, доцент, Волгоградский государственный архитектурно-строительный университет
К ВОПРОСУ О МАТЕМАТИЧЕСКОМ МОДЕЛИРОВАНИИ МОТИВАЦИИ ПРИ ИЗУЧЕНИИ РАЗЛИЧНЫХ ПРОЦЕССОВ
Аннотация
На результаты различных видов человеческой деятельности мотивация оказывает важное, а часто и определяющее, значение. Определены факторы внутренней и внешней мотивации, влияющие на результаты обучения и научной деятельности. Модели мотивации обеспечивают систематизацию и учет взаимосвязей этих факторов. Представляется перспективным использования нейросетевого моделирования. Модели мотивации позволят не только определить ее уровень, но и повлиять на развитие мотивации. В результате человек (например, студент, выпускник вуза, научный сотрудник и т.д.) получит более высокие результаты и может приобрести конкурентные преимущества.
Ключевые слова: математическое моделирование, мотивация.
Haritonova L.P.
PhD in Engineering, associate professor, Volgograd State University of Architecture and Civil Engineering
ON THE ISSUE OF MATHEMATICAL MODELING MOTIVATION IN THE STUDY OF DIFFERENT PROCESSES
Abstract
On the results of various kinds of human activity motivation has an important, and often determines the value. The factors of internal and external motivation, influencing the results of teaching and research activities were given. Motivation models provide systematization and keep the relationship of these factors. It seems promising to use the neural network modeling. Motivation models will not only determine its level, but also give an affect to the development of motivation. As a result a person (eg, a student, a graduate of the university, researcher, etc.) will get better results and can gain a competitive advantage. Keywords: mathematical modeling, motivation.
Чтобы иметь высокий спрос на рынке труда выпускник вуза, а еще ранее студент, должен быть мотивирован [1] на приобретение конкурентных преимуществ. В целом творческий потенциал человека в работе [2] определяется как неразрывная совокупность интеллекта, креативности, мотивации, и квалификации. Безусловно, построение математических моделей мотивации при изучении различных процессов - сложный вопрос. Рассмотрим только ряд подходов к его решению, а также процессов, на результаты которых мотивация оказывает важное, а то и определяющее влияние.
Мотивация сильно влияет на результаты обучения. Как указывается в работе [3] важен вопрос о том, возможно ли научить и научиться мотивации. Требуется разработка курсов, обеспечивающих в студентах развитие мотивации, которая тесно связана с самообладанием и самооценкой. Психологи различают внутреннюю и внешнюю мотивацию. Внутренняя мотивация зависит от личных, индивидуальных потребностей. Студенты хотят учиться вследствие желания удовлетворения личных интересов и целей. На развитие внутренней мотивации [4] в значительной мере может повлиять преподаватель, предлагая студентам интересующие их темы и увлекая интересной информацией, например результатами собственной научной деятельности [5]. Внешняя мотивация вызвана воздействиями на студента родственниками, желанием учиться в престижном вузе, стремлением предотвращения неудачи, страхом плохой оценки, вероятностью отчисления из вуза или потери стипендии или желанием получить поощрение в самом разном виде.
Рассмотрим вопрос влияния мотивации на распространение знаний в вузе. В работе [6] приведена математическая модель распространения знаний в студенческой среде в виде функции от мотивации. Эта модель получена основе приведенной в работе [7] формулы, не учитывающей влияния мотивации. Модель обязательно должна учитывать наличие мотивации к обучению, которая меняется со временем у каждого студента от практически равной нулю (студент поступил в вуз, так как этого хотели его родители) до самой сильной (равной единице) при ярко выраженном стремлении к получению образования именно по выбранной им самим специальности; от весьма неопределенной мотивации у студентов дневной формы обучения, до высокой потребности, которая, часто имеется у студентов дистанционной формы обучения, работающих по выбранной специальности. Уровень мотивации может сильно изменяться у одного и того же студента при изучении различных дисциплин от иногда невысоких значений при изучении общеобразовательных предметов до самых высоких величин при изучении специальных дисциплин. Пусть ![]() - значение мотивации. Так как мотивация обычно изменяется с течение времени, т.е.
- значение мотивации. Так как мотивация обычно изменяется с течение времени, т.е. ![]() =
= ![]() , в результате получаем следующую математическую модель.
, в результате получаем следующую математическую модель.
где ![]() - время;
- время; ![]() - i=1,2,3, … , n - уровень знаний и i-ой группе;
- i=1,2,3, … , n - уровень знаний и i-ой группе; ![]() -предельное значение уровня знаний;
-предельное значение уровня знаний; ![]() ,
, ![]() ,
, ![]() - - коэффициенты усвоения знаний, забывания и управляемости в i-ой группе соответственно;
- - коэффициенты усвоения знаний, забывания и управляемости в i-ой группе соответственно; ![]() - коэффициент влияния j-ой группы на i-ю группу.
- коэффициент влияния j-ой группы на i-ю группу. ![]() и
и ![]() - управляющее воздействие и предел управляющего воздействия.
- управляющее воздействие и предел управляющего воздействия.
Остановимся далее на вопросе уровня мотивации при научной деятельности. Уровень мотивации может характериззвать удовлетворение, получаемое человеком от научной деятельности. Компоненты научного потенциала личности как правило изменяются в зависимости от возраста и вида деятельности. Мотивация является одним из наиболее подвижных. Как указано в работе [2] она определяет время, уделяемое научной деятельности. Очень велики роль внешней среды, а также стимулирование в зависимости от достигнутых результатов и квалификации. В работе [2] предлагается скорость изменения суммарного уровня мотивации творческой личности принимать в зависимости от следующих факторов: - внутреннего мотивационного импульса (по К. Юнгу- ощущение личного предназначения); - эмоций (например усталости при выполнении необходимой, но рутинной работы, или воодушевления при удачных попытках найти новые идеи, т.е. при различных элементах творческой деятельности); - утомления; - внешнего стимулирования научной деятельности (признания в обществе, наград, а конце концов и материального стимулирования и проч.).
Дифференциальное уравнение для расчета скорости изменения суммарного уровня мотивации M творческой личности [2] предлагается записать в виде:
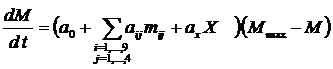 , (2)
где
, (2)
где ![]() - время;
- время; ![]() ,
, ![]() ,
, ![]() - весовые коэффициенты, которые учитывают относительную значимость факторов;
- весовые коэффициенты, которые учитывают относительную значимость факторов; ![]() - физиологически предельный уровень мотивации;
- физиологически предельный уровень мотивации;![]() - квалификация исследователя;
- квалификация исследователя; ![]() - множитель, учитывающий снижение темпа уровня мотивации в при приближении к физиологически возможному предельному уровню мотивации; i= 1, … , 9 – номера функций исследовательской деятельности (от поиска темы до анализа полученного решения; j = 1, … , 4 – номера уровней научно- исследовательской деятельности (от научного сотрудника, занимающегося выполнением фрагмента работы, до членов академий наук, руководящих направлением);
- множитель, учитывающий снижение темпа уровня мотивации в при приближении к физиологически возможному предельному уровню мотивации; i= 1, … , 9 – номера функций исследовательской деятельности (от поиска темы до анализа полученного решения; j = 1, … , 4 – номера уровней научно- исследовательской деятельности (от научного сотрудника, занимающегося выполнением фрагмента работы, до членов академий наук, руководящих направлением); ![]() - текущее среднее время, которое было отведено соответствующему элементу научной работы. Последняя формула является составной частью математической модели, которая представляет собой задачу оптимального управления и решается с использованием аппарата линейного программирования. К сожалению, судя по всему весовые коэффициенты, которые учитывают относительную значимость факторов, определяются экспертно, то есть весьма субъективно. Вместе с тем нам представляется, что структура формулы (2) может быть использована также для расчета скорости изменения уровня мотивации в процессе обучения или некоторых других видах человеческой деятельности (к примеру - в спорте). Например, для процесса обучения в качестве i можно рассматривать: получение задачи; выбор метода и формулы, с помощью которых можно найти решение; анализ полученного результата. В качестве j- номера выполняемых заданий (например, при изучении одной темы возможны как задания простейшей, средней и т.д. сложности, так и инновационные задания, требующие специальных исследований). При разработке математических моделей мотивации возможности строгой формализации объектов моделирования ограничены. При этом получение таких моделей представляется весьма перспективным, так как обеспечивает систематизацию и учет взаимосвязи динамики большого количества факторов, от которых зависит мотивация. Поэтому аналогично [2] представляется целесообразным использование математического аппарата работы с неопределенной информацией. Например, подход, позволяющий объединять полученные из разных соображений разнокачественные оценки, кроме количественных также качественные шкалы (ПРИНН - метод для принятия решений в условиях неопределенности). Но в целом, задача математического моделирования мотивации требует дальнейших исследований, и в связи с огромным количеством факторов, часть из которых перечислена выше, и выходит за рамки настоящей статьи. Ценность имеет даже не само моделирование как таковое. Важно прогнозирование полученных результатов. Сейчас насчитывается порядка 100 методов прогнозирования. Представляется перспективным использование нейросетевого моделирования для установления сложных закономерностей, которые не могут быть обнаружены известными линейными методами.
- текущее среднее время, которое было отведено соответствующему элементу научной работы. Последняя формула является составной частью математической модели, которая представляет собой задачу оптимального управления и решается с использованием аппарата линейного программирования. К сожалению, судя по всему весовые коэффициенты, которые учитывают относительную значимость факторов, определяются экспертно, то есть весьма субъективно. Вместе с тем нам представляется, что структура формулы (2) может быть использована также для расчета скорости изменения уровня мотивации в процессе обучения или некоторых других видах человеческой деятельности (к примеру - в спорте). Например, для процесса обучения в качестве i можно рассматривать: получение задачи; выбор метода и формулы, с помощью которых можно найти решение; анализ полученного результата. В качестве j- номера выполняемых заданий (например, при изучении одной темы возможны как задания простейшей, средней и т.д. сложности, так и инновационные задания, требующие специальных исследований). При разработке математических моделей мотивации возможности строгой формализации объектов моделирования ограничены. При этом получение таких моделей представляется весьма перспективным, так как обеспечивает систематизацию и учет взаимосвязи динамики большого количества факторов, от которых зависит мотивация. Поэтому аналогично [2] представляется целесообразным использование математического аппарата работы с неопределенной информацией. Например, подход, позволяющий объединять полученные из разных соображений разнокачественные оценки, кроме количественных также качественные шкалы (ПРИНН - метод для принятия решений в условиях неопределенности). Но в целом, задача математического моделирования мотивации требует дальнейших исследований, и в связи с огромным количеством факторов, часть из которых перечислена выше, и выходит за рамки настоящей статьи. Ценность имеет даже не само моделирование как таковое. Важно прогнозирование полученных результатов. Сейчас насчитывается порядка 100 методов прогнозирования. Представляется перспективным использование нейросетевого моделирования для установления сложных закономерностей, которые не могут быть обнаружены известными линейными методами.
Литература
- Харитонова Л.П. Концептуальные основы измерения и повышения уровня знаний и мотивационные аспекты при формировании профессионального мышления в высшей школе /Известия ВолгГТУ: межвуз.сб. науч. ст. № 8. (Сер. Новые образовательные системы и технологии обучения в вузе. Вып. 1). Волгоград.2004. С.84 - 86.
- Пиявский С.А. Математическое моделирование управляемого развития научных способностей. Известия Российской академии наук. Теория и системы управление. 2000. №3.С.100-106.
- Baranovskaya T.A. Self –Regulation Skills Several Ways of Helping Students Develop Self-Regulated Learning. Journal of Language & Education. Volume 1. Issue1. 2015. p. 37-44.
- Mezei G. Motivation and self-regulated learning: a case-study of a pre-intermediate and an upper-it-ermediate adult student. Working papers in language pedagogy. 2. 2008. p.79-104.
- Харитонова Л.П. Об использовании элементов научных исследований процессов различной физической природы, в том числе по теории тепломассообмена и аэродинамики, при преподавании высшей математики. Известия ВГТУ. Новые образовательные системы и технологии обучения в вузе / ВолгГТУ. Волгоград.2013.Том 10. №13 (116). С.150-152.
- Харитонова Л.П. К вопросу о математическом моделировании одного процесса. В сборнике: Наука и образование: архитектура, градостроительство и строительство. Материалы Международной конференции, посвященной 80-летию строительного образования и 40-летию архитектурного образования Волгоградской области. 2010. С. 85-87.е
- Бойков И.В. Суздалева И.А. Об одной модели образования // Известия высших учебных заведений. Поволжский регион. № 5. 2006. С. 82 - 86.
References
- Haritonova L.P. Konceptual'nye osnovy izmerenija i povyshenija urovnja znanij i motivacionnye aspekty pri formirovanii professional'nogo myshlenija v vysshej shkole /Izvestija VolgGTU: mezhvuz.sb. nauch. st. № 8. (Ser. Novye obrazovatel'nye sistemy i tehnologii obuchenija v vuze. Vyp. 1). Volgograd.2004. S.84 - 86.
- Pijavskij S.A. Matematicheskoe modelirovanie upravljaemogo razvitija nauchnyh sposobnostej. Izvestija Rossijskoj akademii nauk. Teorija i sistemy upravlenie. 2000. №3.S.100-106.
- Baranovskaya T.A. Self –Regulation Skills Several Ways of Helping Students Develop Self-Regulated Learning. Journal of Language & Education. Volume 1. Issue1. 2015. p. 37-44.
- Mezei G. Motivation and self-regulated learning: a case-study of a pre-intermediate and an upper-it-ermediate adult student. Working papers in language pedagogy. 2. 2008. p.79-104.
- Haritonova L.P. Ob ispol'zovanii jelementov nauchnyh issledovanij processov razlichnoj fizicheskoj prirody, v tom chisle po teorii teplomassoobmena i ajerodinamiki, pri prepodavanii vysshej matematiki. Izvestija VGTU. Novye obrazovatel'nye sistemy i tehnologii obuchenija v vuze / VolgGTU. Volgograd.2013.Tom 10. №13 (116). S.150-152.
- Haritonova L.P. K voprosu o matematicheskom modelirovanii odnogo processa. V sbornike: Nauka i obrazovanie: arhitektura, gradostroitel'stvo i stroitel'stvo. Materialy Mezhdunarodnoj konferencii, posvjashhennoj 80-letiju stroitel'nogo obrazovanija i 40-letiju arhitekturnogo obrazovanija Volgogradskoj oblasti. 2010. S. 85-87.
- Bojkov I.V. Suzdaleva I.A. Ob odnoj modeli obrazovanija // Izvestija vysshih uchebnyh zavedenij. Povolzhskij region. № 5. 2006. S. 82 - 86.