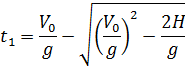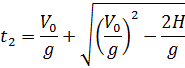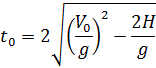HEURISTIC AND ALGORITHMIC APPROACHES IN SOLVING PROBLEMS
Палий Н.Ю.
Кандидат педагогических наук, Кубанский государственный университет
ЭВРИСТИЧЕСКИЙ И АЛГОРИТМИЧЕСКИЙ ПОДХОДЫ ПРИ РЕШЕНИИ ЗАДАЧ
Аннотация
В статье рассматриваются эвристический и алгоритмический подходы при решении задач в процессе обучения физике школьников и студентов, приводятся примеры использования нетривиальных методов решения классических физических задач, показывается, что для использования эвристического подхода к решению задач необходимо построить правильную физическую модель рассматриваемого процесса, также отмечается необходимость показывать обучающимся различные подходы к решению одних и тех же задач.
Ключевые слова: эвристический подход, алгоритмический подход, методика решения задач.
Palij N.Yu.
PhD in Pedagogy, Kuban State University
HEURISTIC AND ALGORITHMIC APPROACHES IN SOLVING PROBLEMS
Abstract
The article considers heuristic and algorithmic approaches in solving problems in a course of physics for pupils or students, we give examples of using of non-trivial methods for solving classical problems, it is shown that the heuristic approach to solving the problems it is necessary to build the correct physical model of the process, also noted the need to show pupils and students different approaches to solving the same problems.
Keywords: heuristic approach, algorithmic approach, a technique for solving problems.
При обучении решению физических задач всегда следует руководствоваться принципом, что правильный физический результат может быть получен разными способами. Справедливо и обратное: результат, полученный при определенном способе рассмотрения и не повторяющийся при использовании других подходов, как правило, неверен и является следствием использованных приближений, не отражая суть изучаемого явления.
Мастерство преподавателя при обучении физике определяется, прежде всего, тем обстоятельством, на скольких «разных языках» он может описать рассматриваемое явление. Поэтому при обучении решению задач важно возможно шире сочетать алгоритмические и эвристические подходы, отдавая сначала предпочтение алгоритмическому подходу с целью выработки и закрепления необходимых технических навыков и умений, а затем делая все больший и больший крен в сторону эвристического подхода с целью максимального развития творческих способностей учащихся. Рассмотрим конкретный пример сочетания эвристического и алгоритмического подходов при решении определенной физической задачи.
Тело бросают вертикально вверх. Наблюдатель измеряет промежуток времени t0 между двумя моментами, когда тело проходит точку А, находящуюся на высоте Н. Определить начальную скорость V0 брошенного тела.
Алгоритмический путь решения этой задачи начинается с использования уравнения движения тела с постоянным ускорением свободного падения g. В проекции на направленную вверх вертикальную ось оно имеет вид:
где h – высота относительно поверхности земли той точки, где находится тело спустя промежуток времени t после начала движения. В условии задачи говорится о нахождении тела на заданной высоте H. Поэтому, подставляя в (1) h=H, можно найти время t, когда тело находится на этой высоте. Уравнение (1) квадратное относительно t. Решая его, находим:
По условию задачи тело побывало на высоте Н дважды. Это значит, что дискриминант D в (2) положителен:
откуда ![]() – высота Н меньше максимальной высоты подъема тела
– высота Н меньше максимальной высоты подъема тела ![]() , брошенного вертикально с начальной скоростью V0. Итак, только из того факта, что тело пребывало на высоте дважды, можно получить некоторую оценку для величины начальной скорости V0:
, брошенного вертикально с начальной скоростью V0. Итак, только из того факта, что тело пребывало на высоте дважды, можно получить некоторую оценку для величины начальной скорости V0: ![]() .
.
Теперь задумаемся над смыслом каждого из корней (2) квадратного уравнения. Поскольку ![]() есть время подъема тела на максимальную высоту, то значение t1 со знаком «минус» перед радикалом соответствует времени подъема тела на заданную высоту Н, а значение t2 со знаком «плюс» перед радикалом определяет время, по истечение которого тело снова окажется на высоте Н, спускаясь вниз:
есть время подъема тела на максимальную высоту, то значение t1 со знаком «минус» перед радикалом соответствует времени подъема тела на заданную высоту Н, а значение t2 со знаком «плюс» перед радикалом определяет время, по истечение которого тело снова окажется на высоте Н, спускаясь вниз:
Очевидно, что заданный в условии промежуток времени t0 равен разности значений t2 и t1:
Подставим сюда значения t2 и t1, имеем:
откуда:
При эвристическом подходе к решению задачи можно обойтись без использования исходного уравнения (1). Для этого достаточно только сообразить, что тело поднимается вверх от точки А на высоту Н в течение времени ![]() , останавливается, а затем падает до точки А в течение времени
, останавливается, а затем падает до точки А в течение времени ![]() . Падая до точки А, тело успевает набрать скорость
. Падая до точки А, тело успевает набрать скорость ![]() . Теперь легко найти скорость V, которую тело наберет, пройдя путь равный Н, от точки А до поверхности земли:
. Теперь легко найти скорость V, которую тело наберет, пройдя путь равный Н, от точки А до поверхности земли:
Очевидно, что эта скорость V равна скорости V0, с которой тело было брошено вертикально вверх. Решение, основанное на эвристическом подходе, оказывается таким же строгим, как и приведенное выше решение, ибо использует только факт одинаковости времени подъема и падения тела, брошенного вертикально вверх, и кинематическое соотношение между перемещением, скоростями в начальной и конечной точках и ускорением при равнопеременном движении. Применительно к движению в поле земного тяготения это соотношение эквивалентно закону сохранения энергии.
Эвристический подход часто позволяет получить ответ, вообще не выписывая никаких соотношений в явном виде. Рассмотрим задачу:
Через неподвижный брусок перекинута нерастяжимая нить, к концам которой прикреплены грузы с массами m и M, причем m<<M. Найти силу натяжения нити при движении грузов, пренебрегая трением, массами блоков и нити.
Вместо того, чтобы выписывать уравнения движения обоих грузов, можно сообразить, что при указанном в условии задачи неравенстве m<<M тяжелый груз будет падать практически свободно, т.е. почти с ускорением g. Но тогда в силу нерастяжимости нити легкий груз будет подниматься с таким же по величине ускорением, направленным вверх. Для этого действующая на него со стороны нити сила должна быть вдвое больше силы тяжести mg. Поэтому сила натяжения нити T=2mg. Так как массой блока можно пренебречь, то сила натяжения нити одинакова по обе стороны блока.
Эвристический подход к решению физических задач тесно связан с вопросом построения физической модели изучаемого явления. Эвристический подход заключается в выборе нетривиальной модели рассматриваемого процесса.
Литература
- Бутиков Е.И., Быков А.А., Кондратьев А.С. Физика в примерах и задачах. М. – СПб: Издательство МЦНМО – Петроглиф, 2015. 516 с.
- Канн К.Б. Курс общей физики. М.: Курс ИНФРА-М, 2015. 360 с.
- Палий Н.Ю. Методика преподавания физики на подготовительном отделении: учебное пособие для учителей. Краснодар, 2011. 74 с.
References
- Butikov E.I., Byikov A.A., Kondratev A.S. Fizika v primerah i zadachah. – SPb: Izdatelstvo MTsNMO – Petroglif, 2015. 516 s.
- Kann K.B. Kurs obschey fiziki. M.: Kurs INFRA-M, 2015. 360 s.
- Paliy N.Yu. Metodika prepodavaniya fiziki na podgotovitelnom otdelenii: uchebnoe posobie dlya uchiteley. Krasnodar, 2011. 74 s.