A MATHEMATICAL MODEL OF RAILWAY TRACK ON APPROACHES TO BRIDGES TAKING INTO ACCOUNT VARIABLE STIFFNESS OF THE UNDER-RAIL FOUNDATION
A MATHEMATICAL MODEL OF RAILWAY TRACK ON APPROACHES TO BRIDGES TAKING INTO ACCOUNT VARIABLE STIFFNESS OF THE UNDER-RAIL FOUNDATION
Abstract
The article is dedicated to the development of a mathematical model of railway track on approaches to bridges, taking into account variable stiffness of the under-rail foundation. The refined solution is presented, which makes it possible to increase the accuracy of the predicted deflection of the rail track considering additional factors previously not taken into account in the calculations, which will ensure the smooth movement of rolling stock, increase the overhaul life of the track, and also make it possible to predict the choice of material and type of base construction when switching from ballastless to ballastless track. The obtained refined solutions also make it possible to minimize the value of the specific resistance of the rolling stock, as well as the amount of electricity and fuel consumed. The presented work is relevant within the framework of this research.
1. Введение
Как известно из работ , , основной характеристикой для оценки напряженно-деформируемого состояния железнодорожного пути является модуль упругости, который при расчетах на прочность позволяет определить связь между деформацией и прикладываемой нагрузкой на железнодорожный путь. В классических расчетах на прочность, представленных в работах , подразумевается, что жесткость подрельсового основания величина равномерно распределенная. Точность величины модуля упругости напрямую влияет на расчеты прогиба плети и напряжений, возникающих в ней. На значение модуля упругости железнодорожного пути влияют большое количество факторов: тип шпал, прокладок, земляного полотна, балластного слоя и т.д., работающих как одна система, при этом с неравной степенью их вклада в общую деформацию.
Неравноупругость в подрельсовом основании может быть вызвана нарушением состояния железнодорожного пути: интенсивное и тяжеловесное движение составов, просадки зачет слабых грунтов основания, загрязнение балласта, нарушение скреплений и пр., а также самой конструкцией железнодорожного пути в местах примыкания к мостам и путепроводам (конструкции переменной жесткости) для плавного перехода. Одним из наиболее характерных примеров изменения модуля упругости является конструкция перехода обыкновенного пути на балласте в безбалластный путь на плитах БМП мостов, с использованием переходных участков .
Целью работы является усовершенствование методов расчета пути на прочность с учетом варьирования величины модуля упругости на подходах к мостам и путепроводам, а также построение математической модели зависимости модуля упругости и прогиба рельсовой плети.
2. Методы и принципы исследования
За основу расчета рельсового пути на прочность с учетом переменной жесткости основания воспользуемся расчетом рельсовой нити, где основание под ней равноупругое, а нагрузка, приложенная к плети вертикальная, при этом зависимость модуля упругости и прогиба рельсовой плети – линейная величина , , . В нашем случае при решении задачи учитывается случай переменного модуля упругости основания с нелинейной поправкой вдоль оси y. Преобразование величины равно-упругого основания решается путем определения малого параметра. Далее определяется влияние неравноупругости подрельсового основания на значение максимального прогиба.
Исходными данными для решения поставленной задачи являются следующие допущения: рельсовая плеть – балка длина которой стремится к бесконечности, подрельсовое основание неоднородное и неравноупругое, воздействие вертикальной нагрузки Q постоянное, также значение модуля упругости основания представлено нелинейной характеристикой от деформации рельсовой плети. В рассматриваемом случае решение дифференциального уравнения для вертикального перемещения рельса примет следующий вид:
где Е – значение модуля упругости стальной балки; J – момент инерции балки; у – прогиб балки; u(y) – зависимость варьирования модуля упругости подрельсового основания по переменной у.
При решении задачи примем, что u(y) – это нелинейная функция от у
Где – константы,
– экспериментальные постоянные величины.
Обозначим следующие выражения:
Для нахождения у+, у– решим следующие уравнения (4), учитывая следующие граничные условия (5):
Задача решается в виде:
Учитывая (4–7) с точностью до членов О(ε2), получим следующее:
Полученное решение примет вид:
Нахождение (10)–(11) осуществляется с помощью следующих значений: для определения
Используя (12) получим:
Ниже представлены решения выражений (10) с учетом максимальных значений для :
Приминая во внимание (13), найдем:
Учитывая изложенные выше выражения (10)–(11) записывается следующим образом:
где уч+ и уч– определяются выражениями
Подставляя (16) в (10), определим
Используя граничные условия (11) найдем с1 и с2
Точное решение задачи до О(ε2):
3. Основные результаты
На основании полученных значений построим график зависимости безразмерного значения прогиба рельсовой плети с учетом неравноупругого и равноупругого основания (рис.1, рис. 2, рис.3):
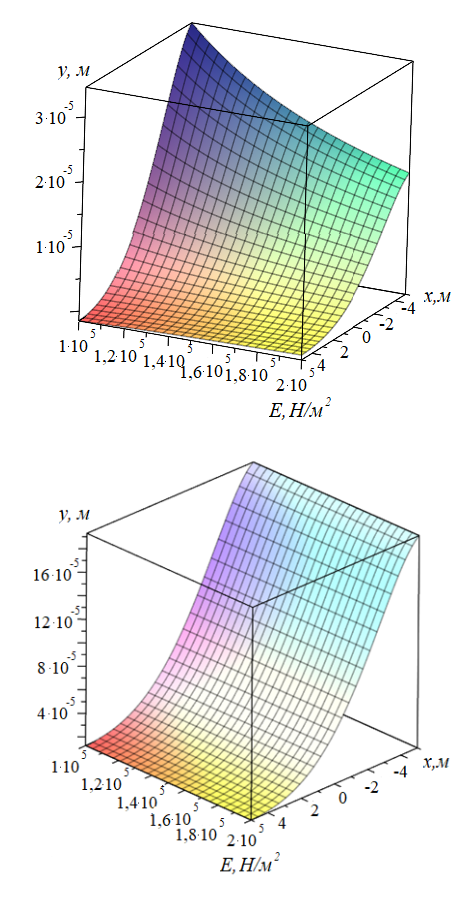
Рисунок 1 - График зависимости значения прогиба рельсовой плети и изменения значения модуля упругости рельса с учетом:
а – равноупругого основания; б – неравноупругого основания
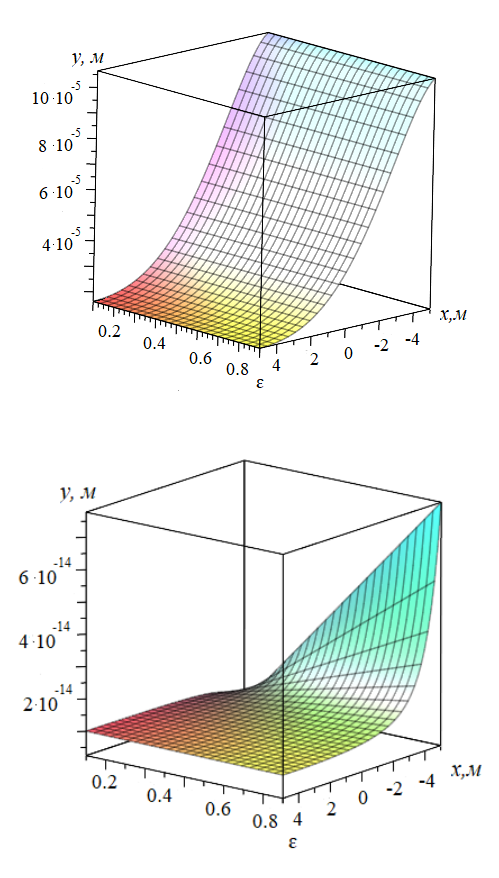
Рисунок 2 - График зависимости значения прогиба рельсовой плети и изменения величины неравномерности подрельсового основания с учетом:
а – равноупругого основания; б – неравноупругого основания
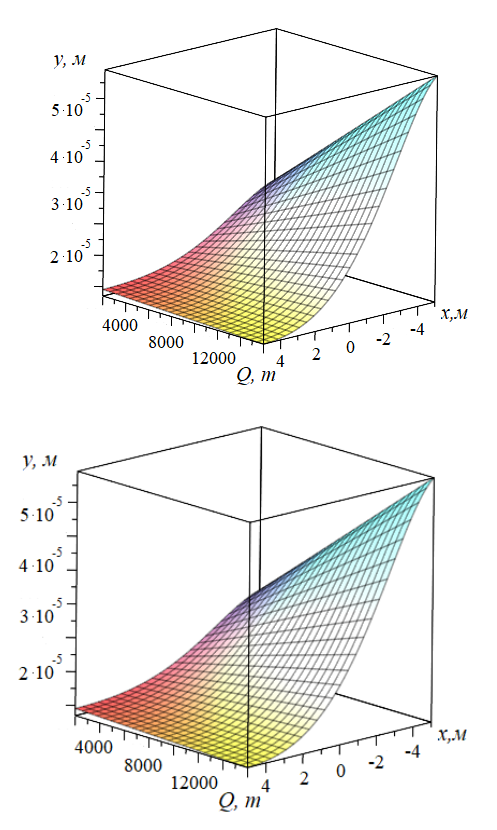
Рисунок 3 - График зависимости значения прогиба рельсовой плети и изменения веса сотостава с учетом:
а – равноупругого основания; б – неравноупругого основания
4. Заключение
1. Найденная расчетная модель позволяет усовершенствовать методику расчета пути на прочность с учетом варьирования величины модуля упругости на подходах к мостам и путепроводам.
2. Построенная математическая модель наглядно показывает повышение точности расчетов.
3. Полученные значения в результаты расчета значительно снижают величину удельного сопротивления поезда, объем потребляемого электричества в случае электровозной тяги и топлива в случае тепловозной тяги, а также позволяют оптимизировать и прогнозировать значение прогиба поверхности катания колеса.
