Toward Robust Stability Margin Evaluation in Continuous and Discrete Systems
Toward Robust Stability Margin Evaluation in Continuous and Discrete Systems
Abstract
The work presents the problem of determining the robust stability margin, i.e. the stability margin in conditions of uncertainty in setting all or part of parameters of continuous and discrete dynamic systems. A procedure for determining the maximum stability margin, based on the introduction of the parameter determining the value of the stability margin into the characteristic equation in explicit form, is suggested. When determining the robust stability of reduced polynomials, the Routh–Hurwitz theorem for continuous dynamical systems and the Korsakov criterion for discrete dynamical systems, as well as the basic statements of the theory of robust stability, which allows to take into account the initial parametric uncertainty, are used. Examples of finding the maximum robust stability margin in concrete continuous dynamical systems with the second and third order characteristic polynomials are presented.
1. Введение
Запасом устойчивости называют количественную характеристику, определяющую степень удаления параметров системы от границы устойчивости . Для нормального функционирования конкретных технических систем необходимость обеспечения достаточного запаса устойчивости является естественной задачей , , . А поскольку точное определение параметров реальной системы часто бывает затруднительно, возникает задача оценивания запасов устойчивости систем с интервальными параметрами (т.е. робастного запаса устойчивости) , . При этом, традиционно при решении задачи определения запасов устойчивости используется критерий Найквиста , .
В настоящей работе рассматривается задача об определении максимального запаса устойчивости в пространстве параметров для непрерывных и дискретных систем с использованием других критериев устойчивости. Пересчет параметра, характеризующего запас устойчивости в динамических системах, в коэффициенты их характеристических уравнений, позволяет использовать известные критерии устойчивости , , , , не только в случае заданного запаса устойчивости, но и распространить их на случай его интервального задания. В качестве примера рассмотрено нахождение максимального робастного запаса устойчивости в непрерывных динамических системах с характеристическими полиномами второго и третьего порядка.
Актуальность указанного подхода связана прежде всего с задачами, где речь идет не только о качественных исследованиях, но и получении некоторых количественных характеристик интервально неопределенных как непрерывных, так и дискретных систем. В частности с задачей получения оценок длительности переходных процессов в интервально неопределенных системах.
2. Запас устойчивости непрерывных систем и метод Рауса-Гурвица
Будем характеризовать запас устойчивости величиной , для которой корни семейства полиномов
удовлетворяют условию . Для того чтобы свести задачу определения
к проблеме Гурвица перейдем на плоскости корней к новому значению
, соответствующему сдвигу мнимой оси на величину
влево. В этом случае полином (1) переходит в полином
коэффициенты которого определяются из тождества
и равны
Известно , что переход корней полинома через прямую
слева направо соответствует нарушению неравенств
и
, где
– предпоследний определитель Гурвица, составленный из коэффициентов полинома
. Поскольку
и не зависит от
, нарушение неравенства
соответствует нарушению неравенства
, т.е. легко проверяется. Нарушение же неравенства
при
легко может быть уставлено с помощью анализа выражения
при условии, что при . Следовательно, для определения максимального значения параметра
необходимо анализировать выражение
при увеличении
, начиная со значения
. Представим при
выражение для
в виде разности
где – члены правой части (5), содержащие
в четных степенях, включая ноль, а
– члены, содержащие
в нечетных степенях. Тогда очевидно, что
где
При такой постановке вопроса является минимальным положительным корнем уравнения
при условии, что
. Необходимо, однако, отметить, что нахождение точного выражения для
затруднительно. Поэтому можно использовать различного рода оценки для
. Одну из таких оценок получим следующим образом.
Представим в виде разности положительных членов
Такое представление всегда возможно, т.к.
и в силу требования о выполнении необходимого условия устойчивости
. То есть появление в (9) отрицательных членов связано только с операцией раскрытия определителя
. При
, согласно (9), имеет место оценка
Здесь черта у и
переносится однотипно на все входящие в них
. Тогда выполнения неравенства
достаточно для утверждения, что
и, следовательно, при
комплексно-сопряженные корни семейства полиномов (1) не могут находиться на прямой
.
Для оценки величины на основе оценки знакоположительности
можно, скажем, считать, что
. Тогда условие знакопостоянства
можно установить на основе анализа величины
, где
а черта у и
переносится однотипно на все входящие в них
и параметр
.
3. Алгоритм оценивания максимального значения робастного запаса устойчивости и его применение к непрерывным системам с характеристическими полиномами второй и третьей степени
Как следует из приведенных выше рассуждений, при достаточными условиями робастной устойчивости полинома (2) являются
Предположим, что при для полинома
в плоскости каких-либо двух выбранных параметров
при интервальности других построена область робастной устойчивости . Для оптимизации качества переходного процесса в системе необходимо определить такое
, чтобы выполнялись соотношения (12). Так как
и
являются полиномами относительно
, процесс определения
можно провести следующим образом:
1) Находим аналитически или с помощью известных алгоритмических процедур корни уравнений и
. Обозначим их через
и
соответственно.
2) Образуем последовательность действительных положительных чисел из этих корней.
3) Определяем .
4) Строим область робастной устойчивости в плоскости параметров при интервальности всех остальных параметров.
1. Пусть характеристическое уравнение имеет вид
После введения величины будем иметь
Для определения имеем два уравнения
Из (15) определяем
Предположим, что . Тогда достаточная граница робастной устойчивости, оптимизирующая качество переходного процесса в системе, будет определяться из уравнения
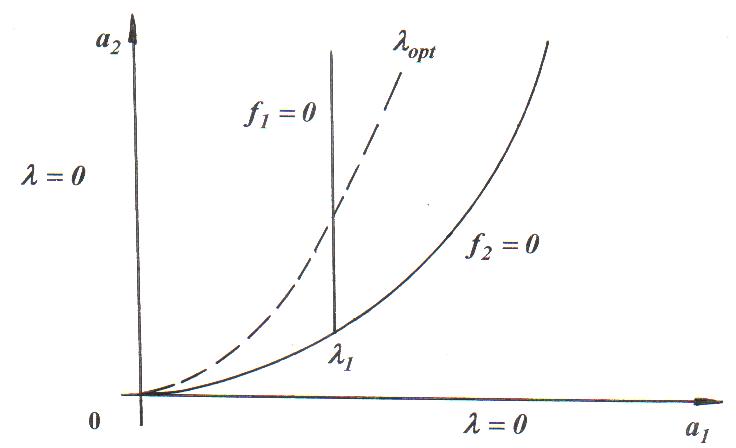
Рисунок 1 - Область робастного запаса устойчивости полинома второй степени
В реальной системе характеристический полином имеет вторую степень, скажем, в математической модели автоколебаний в основной стойке шасси самолета при бесконечной жесткости на кручение, когда момент инерции ориентирующей части стойки относительно оси стойки и коэффициент демпфирования колебаний по углу равны нулю .
2. Предположим теперь, что характеристический полином имеет третью степень, т.е. характеристическое уравнение будет иметь вид
Такая ситуация имеет место в математической модели автоколебаний в основной стойке шасси самолета в случае бесконечной жесткости на кручение без учета момента инерции ориентирующейся части стойки относительно оси стойки . Полином при этом будет иметь вид
где
Уравнения для определения имеют вид
В безразмерных переменных для системы из могут изменяться в пределах
. Тогда, если предположить, что минимальный из
определяется корнем первого уравнения, то, согласно (20), (21),
. А граница, определяющая область робастного запаса устойчивости, задается уравнением
где в качестве параметров для выделения области робастной устойчивости выбраны , а остальные параметры остались интервальными. Уравнение границы (23) можно записать в виде
а если учесть ограничения на параметры, получим
В плоскости выбранных параметров график функции (25) будет иметь вид, приведенный на рисунке 2. Из (25) и рисунка 2 видно, что область робастного запаса устойчивости будет располагаться внутри приведенной кривой.
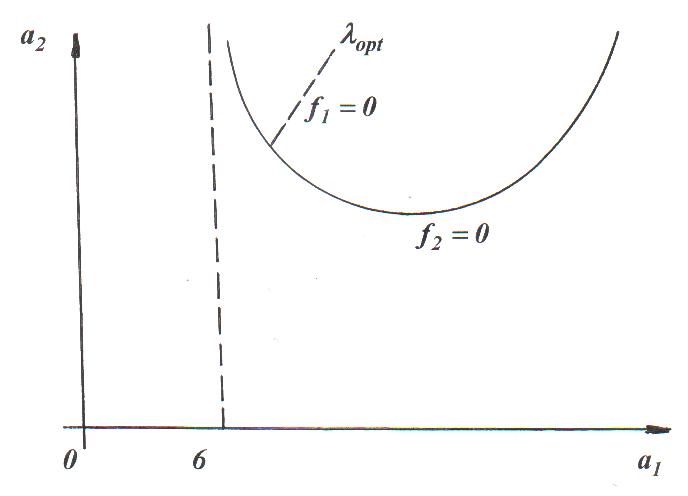
Рисунок 2 - Область робастного запаса устойчивости полинома третьей степени
4. Некоторые предложения по оцениванию максимального значения робастного запаса устойчивости для дискретных систем
Запас устойчивости дискретных динамических систем может быть охарактеризован параметром таким, что
, где
– корни характеристического полинома (1). Поскольку устойчивость (1) имеет место при
, задача обеспечения заданного запаса устойчивости (или определение минимально возможного
) является более общей задачей по отношению к определению условий устойчивости характеристического полинома. Параметр
можно ввести формально в (1) за счет замены
. В этом случае при любом
корни полинома должны лежать в единичном круге, т.е. так, как это имеет место при исследовании устойчивости. При таком подходе
где
При использовании критерия Корсакова как для проверки устойчивости относительно единичного круга при
, так и для нахождения возможного значения
такого, что при
устойчив, можно ограничиться анализом условий невыхода в пространстве
за границы области устойчивости. В этом случае расположение в сторону области устойчивости от границ
соответствует выполнению неравенств
и
, где
– матрицы Корсакова полинома
.
Проверка условия на семействе очевидна, т.к для этого необходимо и достаточно, чтобы выполнялось неравенство
, где
Для анализа условия достаточно, чтобы имело место
, где
Процедура определения при попадании на границы
сводится к определению максимального корня
, при котором обращается в ноль правая часть (28) или правая часть (29).
При рассмотрении выполнимости условия с квадратными матрицами
-го порядка вида
после замены основная сложность состоит в нахождении выражения для
. Так в случае
а значит , где
и условие является достаточным для выполнения
. А в случае
т.е. представляет собой уже полином от достаточно высокой степени, и получение оценки
уже является затруднительным, хотя и возможным
И получение достаточных оценок тем сложнее, чем больше .
5. Заключение
В работе приведены результаты разработки оригинальной методики определения значений параметров, при которых достигается максимальный запас устойчивости и, следовательно, минимальная длительность переходных процессов с непрерывных и дискретных системах, допускающих построение линеаризованных математических моделей, в условиях начальной неопределенности параметров. Показано, что при введении в характеристическое уравнение параметра, характеризующего запас устойчивости, исходные коэффициенты оказываются в линейных комбинациях в новых пересчитанных коэффициентах. В результате при решении вопроса о том, является ли запас устойчивости робастным, исследование с помощью реберной теоремы в любом случае превратилось бы из необходимого и достаточного в достаточное. Поэтому приобретает смысл использования более простых достаточных оценок для исследования робастной устойчивости. Такого типа оценки и получены в работе.
