Determination of Power Flow over a Transmission Line with Arbitrary Point Compensation Devices Using the Four-Pole Circuit Tandem Connection
Determination of Power Flow over a Transmission Line with Arbitrary Point Compensation Devices Using the Four-Pole Circuit Tandem Connection
Abstract
A power transmission line is examined, containing compensation devices, P and Q power extraction devices and reactive power sources (RPS) connected at separate nodes of the line. To calculate the transmission mode, the individual line sections together with the compensating devices are regarded as four-pole circuits with distributed parameters
, .The suggested calculation algorithm is based on the theory of tandem connection of four-pole circuits, which allows to effectively account for any changes in power line parameters and in the initial conditions. In contrast to traditional methods, which include the methods of contour equations and node voltage equations, the proposed approach makes it possible to find the value of power flow in any arbitrary point of the transmission line. The low computational resource requirement of the considered approach should also be noted.
1. Введение
Электроэнергетические системы являются самыми масштабными искусственными объектами, сделанными людьми. Для эффективного функционирования таких систем и адекватной реакции на возникающие аварийные угрозы необходимо полное понимание физических процессов протекающих в этих системах и достоверная оценка параметров в любой точке и любой момент времени.
Кроме своей масштабности, электроэнергетические системы являются комплексными структурами с многослойным иерархическим строением.
На больших расстояниях, что характерно для Восточно-Сибирских и Дальневосточного регионов, передача электроэнергии осуществляется, как правило, с помощью воздушных линий (ВЛ) электропередач.
Чем на большее расстояние необходимо передать электроэнергию, тем больше напряжение требуется для лучшей эффективности энергопередачи. Для поддержания напряжения в заданных пределах, определяемых рамками руководящих документов, служат дополнительные устройства, в частности к этим устройствам относятся источники реактивной мощности(ИРМ) обеспечивающие эту задачу.
Для масштабных электропередач, соединяющих удаленные регионы, возникает задача определения параметров режима не только в выделенных узлах, но и в произвольных сечениях . Существующие методы расчета параметров энергосистемы основаны на методах, представляющих электропередачу как систему с сосредоточенными параметрами, что справедливо для систем с небольшой протяженностью (до 300 км). Большие длины передач переменного тока приводят к необходимости учета волнового характера процессов, происходящих при передаче электрической энергии. Поскольку на частоте 50 Гц длина электромагнитной полуволны (сдвиг по фазе на 180°) в ВЛ составляет 3000 км, то при длинах свыше 300 км представление линий электропередач в виде четырехполюсника с сосредоточенными параметрами приводит не только к большой погрешности расчетов, но и к качественно неверным выводам
, . Анализ и расчеты режимов ДЭП должны выполняться с учетом распределенности параметров вдоль линии.Рассмотрим компенсированную электропередачу, для которой принимаются следующие условия:
а) схему электропередачи (рисунок 1) моделируют в виде каскада n четырехполюсников (рисунок 2), представляющих участки линии электропередачи с распределенными параметрами, компенсирующие устройства, точки промежуточного отбора мощности и ИРМ;
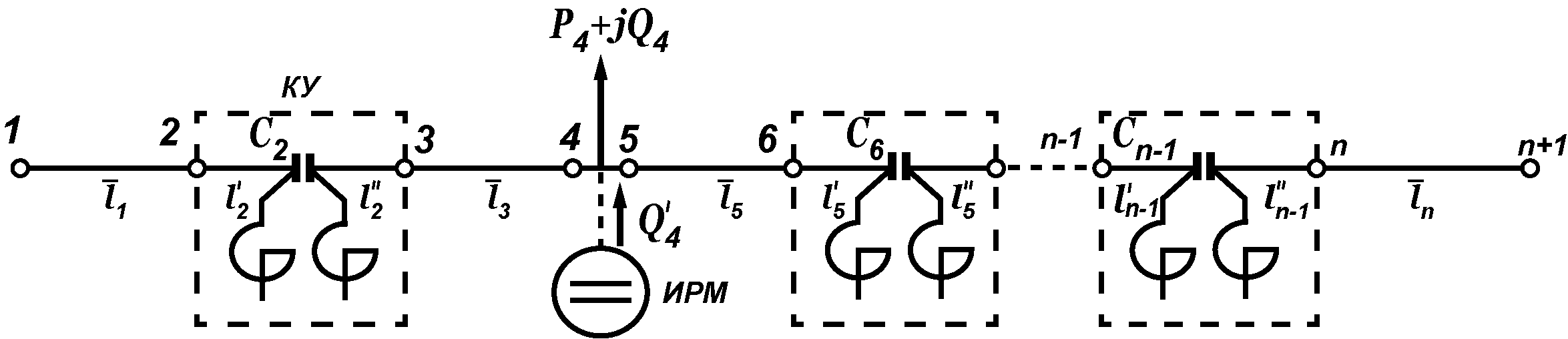
Рисунок 1 - Схема электропередачи с компенсирующими устройствами

Рисунок 2 - Каскад последовательно соединенных четырехполюсников
в) параметры компенсирующих устройств;
г) активная и реактивная мощности отбора, представленные в виде постоянных сопротивлений и
или в виде статических характеристик, величина реактивной мощности
в узлах подключения ИРМ;
д) параметры режима: активная () и реактивная (
) мощности начала (
) или конца (
) линии, модуль (
) и фаза (
) напряжения конца (
) или начала (
) линии, причем
;
е) ограничения в промежуточных узлах компенсированной линии по напряжению – .
Требуется определить параметры режима в любой произвольной точке линии, в том числе в узлах
.
2. Математическая модель эквиалентного четырехполюсника
Представление схемы замещения в виде каскада последовательно соединенных четырехполюсников (рисунок 2) позволяет записать уравнения режима отдельных составных четырехполюсников в виде зависимостей:
здесь и
– комплексные напряжения и токи; 1, 2 – индексы входа и выхода четырехполюсника.
Матрица коэффициентов уравнения (1) имеет следующий вид:
- для четырехполюсников, представляющих участки линии с распределенными параметрами
где – индекс участка линии,
и
– волновое сопротивление и коэффициент распространения, соответственно, которые вычисляются из соотношений:
для четырехполюсников, представляющих компенсирующие устройства:
здесь – параметры элементов
-образной схемы замещения компенсирующего устройства
;
для четырехполюсников, представляющих промежуточный отбор мощности и мощность ИРМ:
где и
– параметры, учитывающие отбор мощности и вычисляемые по заданным статическим характеристикам на заданном шаге итерации,
- мощность ИРМ,
– индекс узла линии, в котором установлено устройство компенсации или подключена нагрузка.
Матрица эквивалентного четырехполюсника (рисунок 3) представляется в виде произведения матриц
элементарных четырехполюсников, в виде:
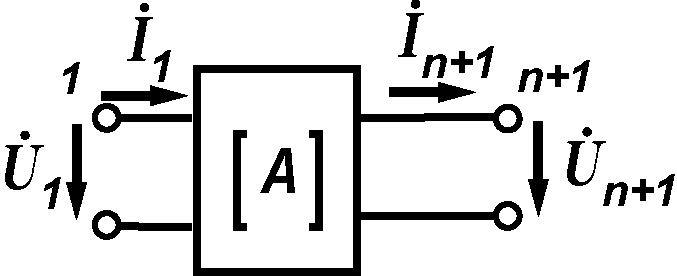
Рисунок 3 - эквивалентный четырехполюсник
где – индексы входа (1) и выхода (
) эквивалентного четырехполюсника;
– элемент матрицы
– параметров уравнения (6), вычисляемых по полученной матрице
эквивалентного четырехполюсника:
Уравнения установившегося режима для эквивалентного четырехполюсника запишем в полярной форме:
где
В этих формулах активная и реактивная
мощности в узле
, берутся со знаком минус, что соответствует мощности нагрузки, подключенной к указанному узлу
3. Расчетные соотношения
Для решения системы уравнений (8)-(11) применяем классический итерационный подход. Критерием окончания расчета служит приращение в двух последовательных шагах итерации с последующей проверкой величины заданного небаланса мощностей
и
. По параметрам режима в конце ВЛ можно определить параметры режима в любом из узлов
по выражениям:
где
-параметры
четырехполюсника соответственно
В начале расчета в выражениях (12)-(15) индекс принимает значения
– индекса узла приемного конца линии – соответственно в качестве начальных параметров принимаются
конца электропередачи. В последующих итерациях применяются те же соотношения (12)-(15) с подстановкой в них параметров
соответствующего четырехполюсника и найденных из расчета параметров предыдущего четырехполюсника.
Если отбор мощности задан постоянными сопротивлениями и в узлах выполняются налагаемые ограничения по напряжению, то расчет завершен. При задании отбора мощности статическими характеристиками нагрузки, последние аппроксимируются многочленами второй степени [q, q],
где и
- коэффициенты полиномов, определяемые составом потребителей, верхний индекс
– шаг последовательных приближений.
В соответствии с расчетом напряжений в узлах отбора в первом шаге итерации производится уточнение их мощностей и
, а по ним, соответственно, параметров
и
.
Режим в произвольной точке участка линии с распределенными параметрами, представленного четырехполюсником, находится путем решения системы уравнений
, :где - индекс участка линии в заданной точке
которого необходимо определить параметры режима;
– длина участка линии с распределенными параметрами;
– расстояние от начала соответствующего участка (
) до искомой точки.
4. Апробация рассматриваемого подхода
Рассмотрим применение рассмотренной методики расчета на примере электропередачи 500 кВ Бурейская ГЭС-Хабаровская 2 (рисунок 4).
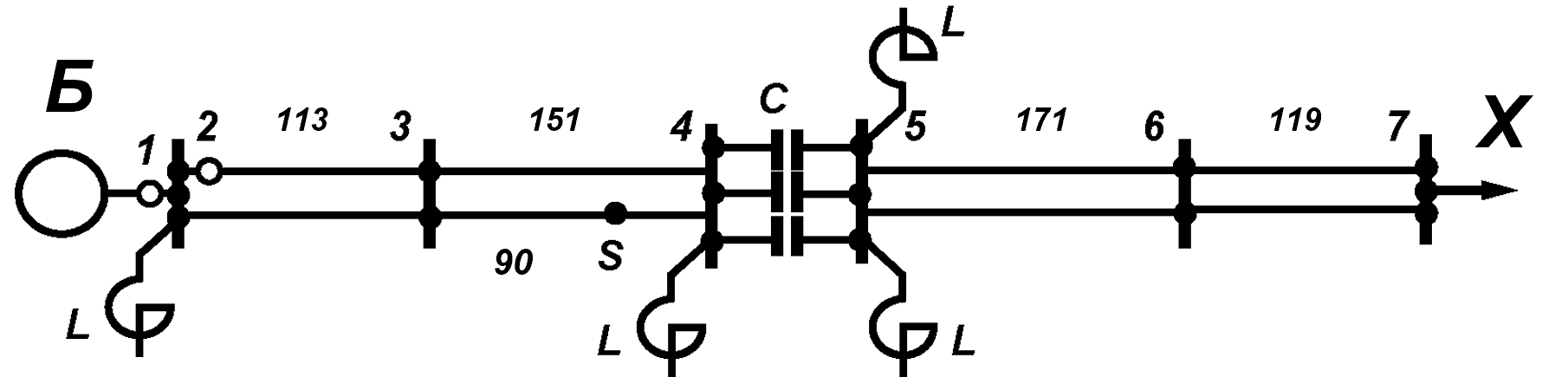
Рисунок 4 - Электропередача Бурейская ГЭС -Хабаровская 2
Параметры режима концов электропередачи: =503,5 кВ;
=0;
=1300 МВт;
=200 МВар.
Результаты расчета сведены в таблицу (таблица 1)
Таблица 1 - Расчет установившегося режима электропередачи Бурейская ГЭС -Хабаровская 2
№ узла | Параметры режима | |||
P, МВт | Q, МВAр | U, кВ |
| |
1 | 1364,5 | -173,4 | 503,5 | 0 |
2 | 1364,5 | -341,1 | 503,5 | 0 |
3 | 1350,5 | -186,7 | 512,5 | -0,1413 |
4 | 1333,0 | 48,0 | 510,7 | -0,3248 |
5 | 1332,8 | -247,8 | 509,7 | -0,1606 |
6 | 1313,4 | 21,0 | 511,4 | -0,3653 |
7 | 1300,0 | 200,0 | 499,9 | -0,5076 |
s | 1340,1 | -49,2 | 513,4 | -0,2496 |
5. Заключение
В работе предложена методика расчета установившегося режима ВЛ, которая учитывает распределенность параметров участков линии и наличие в отдельных узлах устройств компенсации реактивной мощности, а также источников реактивной мощности.
Модель эквивалентного четырехполюсника позволяет определить параметры режима электропередачи в произвольной точке линии, что продемонстрировано на примере электропередачи ЛЭП 500 Бурейская ГЭС – Хабаровская 2.
