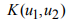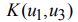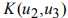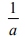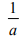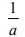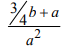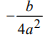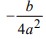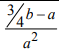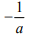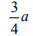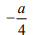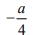THE SECTIONAL CURVATURE OF A THREE-DIMENSIONAL RIEMANNIAN HOMOGENEOUS SPACES

Можей Н.П.

Канд. физ.-мат. наук, доцент, докторант КГУ

СЕКЦИОННАЯ КРИВИЗНА ТРЕХМЕРНЫХ РИМАНОВЫХ ОДНОРОДНЫХ ПРОСТРАНСТВ

Аннотация

Целью работы является описание инвариантных аффинных связностей на трехмерных римановых однородных пространствах. Проведена полная локальная классификация римановых однородных пространств, что эквивалентно описанию эффективных пар алгебр Ли, допускающих инвариантную невырожденную билинейную форму на изотропном модуле. Описаны также все инвариантные аффинные связи вместе с тензорами кривизны и кручения.

Ключевые слова: аффинные связности, однородные пространства, алгебры Ли.

Key words: affine connections, homogeneous spaces, Lie algebras.

Пусть M – многообразие размерности 3, на котором транзитивно действует группа , (M, ) – однородное пространство, G = 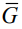 - стабилизатор произвольной точки x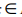M. Пусть  – алгебра Ли группы Ли 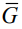, а g – подалгебра, соответствующая подгруппе G. Изучая однородные пространства важно рассматривать не саму группу  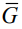а ее образ в Diff(M), другими словами, достаточно рассматривать только эффективные действия группы  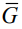на многообразии M. Строение пар групп Ли (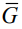, G), соответствующих данной эффективной паре алгебр Ли ( 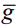g), было описано в [1], т.е. проблема классификации однородных пространств сводится к классификации пар.

В дальнейшем будем предполагать, что 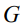 – связная подгруппа, что всегда можно сделать, ограничиваясь локальной точкой зрения, следовательно можно заменить требование 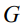-инвариантности на инвариантность относительно соответствующих действий алгебры Ли g. Отображение

называется изотропным представлением подалгебры g. Риманово однородное пространство задается тройкой (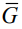, M, ρ), где 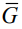- связная группа Ли, M является связным гладким многообразием с транзитивным действием 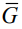, а ρ - инвариантная риманова метрика на M. Инвариантные римановы метрики ρ на M находятся во взаимно-однозначном соответствии с инвариантными симметрическими невырожденными билинейными формами B на G-модуле 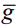/g. Поскольку каждая инвариантная риманова метрика определяет инвариантную аффинную связность, g-модуль 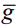/g точен. Ограничимся случаем с ненулевым стабилизатором, т.к. все остальные римановы однородные пространства - только трехмерные группы Ли с инвариантной метрикой. Для нахождения всех изотропно-точных пар нужно классифицировать (с точностью до изоморфизма) все точные трехмерные g-модули U (это эквивалентно классификации всех подалгебр в gl(3, R) с точностью до сопряженности), а далее классифицировать (с точностью до эквивалентности) все пары (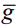, g) такие, что g-модули 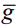/g и U эквивалентны и выбрать пары, допускающие риманову метрику. Далее описать все такие формы B с точностью до индуцированного действия Aut(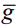, g):

	Таблица умножения	B
1.3.1	e1 u1 u2 u3 e1 0 -u2 u1 0 u1 u2 0 0 0 u2 -u1 0 0 0 u3 0 0 0 0	ε1 0 0 0 ε1 0 0 0 ε2	ε1, ε2=±1
1.3.2	e1  u1  u2  u3  e1  0  -u2  u1  0  u1  u2  0  0  u1  u2  -u1  0  0  u2  u3  0  -u1  -u2  0	ε 0 0  0 ε 0  0 0 a	ε=±1, a≠0
1.3.3	e1  u1  u2  u3  e1  0  -u2  u1  0  u1  u2  0  e1+u3  0  u2  -u1  -e1-u3  0  0  u3  0  0  0  0	a 0 0  0 a 0  0 0 b	ab≠0
1.3.4	e1  u1  u2  u3  e1  0  -u2  u1  0  u1  u2  0  -e1+u3  0  u2  -u1  e1-u3  0  0  u3  0  0  0  0	a 0 0  0 a 0  0 0 b	ab≠0
1.3.5	e1  u1  u2  u3  e1  0  -u2  u1  0  u1  u2  0  e1  0  u2  -u1  -e1  0  0  u3  0  0  0  0	a 0 0  0 a 0  0 0 ±1	a≠0
1.3.6	e1  u1  u2  u3  e1  0  -u2  u1  0  u1  u2  0  -e1  0  u2  -u1  e1  0  0  u3  0  0  0  0	a 0 0  0 a 0  0 0 ±1	a≠0
1.3.7	e1  u1  u2  u3  e1  0  -u2  u1  0  u1  u2  0  u3  0  u2  -u1  -u3  0  0  u3  0  0  0  0	ε 0 0  0 ε 0  0 0 a	ε=±1, a≠0
3.5.1	e1  e2  e3  u1  u2  u3  e1  0  e3  -e2  -u3  0  u1  e2  -e3  0  e1  -u2  u1  0  e3  e2  -e1  0  0  -u3  u2  u1  u3  u2  0  0  0  0  u2  0  -u1  u3  0  0  0  u3  -u1  0  -u2  0  0  0	1 0 0  0 1 0  0 0 1	±
3.5.2	e1  e2  e3  u1  u2  u3  e1  0  e3  -e2  -u3  0  u1  e2  -e3  0  e1  -u2  u1  0  e3  e2  -e1  0  0  -u3  u2  u1  u3  u2  0  0  e2  e1  u2  0  -u1  u3  -e2  0  e3  u3  -u1  0  -u2  -e1  -e3  0	a 0 0  0 a 0  0 0 a	a≠0
3.5.3	e1  e2  e3  u1  u2  u3  e1  0  e3  -e2  -u3  0  u1  e2  -e3  0  e1  -u2  u1  0  e3  e2  -e1  0  0  -u3  u2  u1  u3  u2  0  0  -e2  -e1  u2  0  -u1  u3  e2  0  -e3  u3  -u1  0  -u2  e1  e3  0	a 0 0  0 a 0  0 0 a	a≠0

Здесь e_i - базис g, u_i – дополнительный к g в 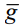(i=1, 2, 3).

Из трехмерных римановых однородных пространств следующие 7 соответствуют классификации Терстона:

- если стабилизаторы точек трехмерны, то тройка 3.5.1. задает евклидово пространство,  3.5.2. --- сферу, а  3.5.3. --- гиперболическое пространство;

- если стабилизаторы одномерны, то  M - 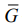-инвариантное расслоение над одной из двумерных геометрий. Метрика определяет связность, при нулевой кривизне связности 1.3.5. задает  S²×E¹ ,  1.3.6. задает  H²×E¹ ,  а при ненулевой кривизне 1.3.3. задает  SL(2, R),  1.3.7. задает  нильгеометрию.

- 1.3.1, 1.3.2, 1.3.4 – подалгебры в  3.5.1, 3.5.2 и 3.5.3 соответственно и задают те же однородные пространства.

Для каждого из указанных выше римановых однородных пространств найдена секционная кривизна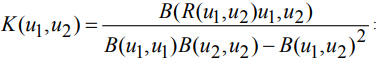

 

Номер тройки
1.3.1.	0	0	0
1.3.2.
1.3.3.
1.3.4.
1.3.5.		0	0
1.3.6.		0	0
1.3.7.
3.5.1.	0	0	0
3.5.2.
3.5.3.