On Quantization of Magnetic Flux

Izbrecht A.R.

doi:10.23670/IRJ.2024.140.7

On Quantization of Magnetic Flux

Research article

Избрехт Александр Рудольфович0000-0001-8018-1144Пенсионер, Екатеринбург, Российская Федерация

Izbrecht A. R.

https://doi.org/10.23670/IRJ.2024.140.7

DOI:

https://doi.org/10.23670/IRJ.2024.140.7

EDN:

IAJNBA

Suggested:

30.09.2023

Accepted:

26.01.2024

Published:

16.02.2024

Issue: № 2 (140), 2024

Rightholder: authors. License: Attribution 4.0 International (CC BY 4.0)

1640

29

XML

PDF

Abstract

The objective of this work is to substantiate the possibility of quantization of the magnetic flux in a superconducting ring and in a superconducting cylinder according to the constant h/2|e| without involving the concept of Cooper pairs of electrons. For this purpose, the well-known de Broglie formula L = h/meV is transformed to the form Ekn = nhIn/2|e| (where Ekn is the kinetic energy of the electron at the n-energy level, In is the current created by the electron at the n- energy level). The position that the value h/2|e| is a quantum of magnetic flux is justified, so the magnetic flux F created by a single electron during its movement along the circumference is determined by the relation F = nh/2|e|. The method of calculation of the magnetic field created by a single electron during its motion along the circumference, based on the property of ideal diamagnetism of superconductors, is presented. The correspondence of the formulas obtained as a result of the application of this method to the values of diameters and wall thicknesses of superconducting tubes in the experiments of Deaver and Feuerbenk, Doll and Nöbauer is shown, and a detailed analysis of these experiments is given. It is concluded that for explaining the quantization of the magnetic flux in accordance with the constant h/2|e| there is no need to refer to the concept of Cooper pairs of electrons.

Keywords:

de Broglie formula, magnetic flux quantum, superconductivity.

1. Введение

Как известно, впервые эффект квантования магнитного потока в сверхпроводящем кольце с током был предсказан Ф. Лондоном

(обычно ссылки даются на его книгу 1950 года ). Ф. Лондон является создателем вместе со своим братом Г. Лондоном первой макроскопической теории сверхпроводимости. Первоначально предсказанная Ф. Лондоном величина кванта потока была

, так как Ф. Лондон исходил из того, что сверхпроводящий ток создается одиночными электронами . Лишь в 1950-е годы была принята модель сверхпроводящего тока, создаваемого спаренными электронами с противоположными спинами и имеющими общий заряд

. Это предположение легло в основу микроскопической теории сверхпроводимости Бардина-Купера-Шриффера (теория БКШ) (1957). Явление квантования магнитного потока было открыто экспериментально Б. С. Дивером и У. М. Фейрбенком и независимо Р. Доллом и М. Нёбауэром в 1961 году. Эксперимент показал, что квант магнитного потока определяется величиной

. Этот результат отличался множителем 1/2 от первоначально предсказанного Ф. Лондоном значения величины кванта магнитного потока

, однако указывал на то, что носителями сверхпроводящего тока являются пары электронов . Объяснение квантования магнитного потока кратно постоянной

считается первым экспериментальным подтверждением теории Бардина-Купера-Шриффера.

Теория БКШ является на сегодняшний день доминирующей теорией, тем не менее полностью удовлетворительная теория сверхпроводимости в настоящее время отсутствует. Так, например, теория БКШ не позволяет объяснить, почему конкретные сверхпроводники имеют ту или иную критическую температуру. В настоящее время известно, что существование изотопического эффекта не является доказательством фононного механизма, ответственного за спаривание электронов. Неудовлетворённость теорией БКШ привела к попыткам создать другие модели («… развитие теории сверхпроводимости стимулировало поиски других механизмов сверхпроводимости»

). Однако, хотя в них рассматривались различные механизмы объединения электронов в пары, к прогрессу в понимании явления сверхпроводимости эти разработки тоже не привели . Поэтому возможность объяснения явления сверхпроводимости без использования концепции объединения электронов в пары является актуальной темой для исследований.

Целью данной работы является обоснование возможности квантования магнитного потока в сверхпроводящем кольце и в сверхпроводящем цилиндре в соответствии с константой

без привлечения концепции куперовских пар электронов

Если такой подход окажется верным, то отпадает необходимость в использовании концепции спаренных электронов для объяснения явления сверхпроводимости.

2. Квантование магнитного потока в атоме модели Бора

Рассмотрим квантование магнитного потока, создаваемого электроном, движущимся по окружности в атоме модели Бора. Для этого преобразуем известную формулу де Бройля (1) к виду (3):

(1)

,

(2)

(3)

В формулы (1 – 3) входят следующие обозначения:

h - постоянная Планка;

– длина волны де Бройля электрона при его движении по окружности в атоме модели Бора;

– масса электрона;

V – поступательная скорость движения электрона по окружности;

Ek – кинетическая энергия электрона;

– время прохождения электроном расстояния вдоль окружности, равного длине волны де Бройля электрона.

Умножим обе части уравнения (3) на целое положительное число n:

(4)

Так как для стабильного движения частицы по окружности необходимо, чтобы на длине окружности укладывалось целое число длин волн де Бройля

, то произведение

определяет период T обращения частицы по окружности, поэтому (4) запишем в виде

(5)

Формула (5) справедлива как для заряженных частиц, так и для частиц, не имеющих заряда. Для электрона, двигающегося по окружности на каком-либо энергетическом уровне в атоме модели Бора формулу (5) преобразуем к виду

(6)

где,

– энергия уровня электрона в атоме Бора (

, так как в атоме Бора энергия уровня электрона по модулю равна его кинетической энергии);

e – заряд электрона;

In – ток, создаваемый электроном при его движении по окружности на каком-либо энергетическом уровне в атоме Бора.

Запишем (6) в виде

(7)

Проверим справедливость формулы (7) на примере атома водорода. Для этого выведем формулу, определяющую величину тока In на какой-либо боровской орбите:

(8)

где, Tn – период обращения электрона по n-ой боровской орбите;

– скорость движения электрона по n-ой боровской орбите ;

– радиус n-ой боровской орбиты .

Найдём теперь отношение

:

(9)

где

– абсолютное значение энергии уровня электрона на n – ой боровской орбите в атоме водорода .

Формула (9) подтверждает справедливость формулы (7).

Из формулы (7) следует, что

(10)

Принято считать, что магнитный поток Ф, создаваемый одиночным электроном, как это было указано во введении к данной статье, квантуется в соответствии с постоянной

. В таком случае величина

равна половине магнитного потока

, а величина, стоящая в правой части уравнения (10), равна энергии магнитного поля

, создаваемого одиночным электроном в рассматриваемом случае, т.е.

(11)

и

(12)

Однако существует и другая точка зрения. В

указано, что магнитный поток через круг радиуса

равен кванту потока

, т.е.

. Далее в в сноске 27 записано: «Мы, следуя Абрикосову , используем для электронов обозначение кванта потока, принятое для сверхпроводников (т.е.

). Иногда вводят отличающееся в два раза значение кванта для нормальных металлов (т.е. Φ0 = h/|e|)».

Если принять величину кванта магнитного потока

, тогда формулы (11) и (12) запишутся в виде

(13)

(14)

или

(15)

То есть, в зависимости от того, какая величина кванта магнитного потока

принята (Φ0 = h/|e| или Φ0=h/2|e|) кинетическая энергия электрона

может быть или равна энергии магнитного поля, создаваемого им при движении по окружности (формула 12), или энергия магнитного поля, создаваемого электроном при движении по окружности, равна половине его кинетической энергии (формула (15)). Этот вывод следует из основной формулы (7).

3. Квантование магнитного потока при движении электронов по циклотронным орбитам

Покажем, что магнитный поток

, создаваемый двигающимся по окружности одиночным электроном, всегда определяется величиной

и, следовательно, квант магнитного потока

равен

.

Допустим, что одиночный электрон под действием силы Лоренца движется по циклотронной орбите в магнитном поле, перпендикулярном плоскости его орбиты. Величина радиуса циклотронной орбиты электрона должна отвечать двум условиям. Первым условием является соответствие радиуса циклотронной орбиты формуле (16)

(16)

где,

– радиус циклотронной орбиты электрона;

– поступательная скорость движения электрона по циклотронной орбите;

– индукция внешнего магнитного поля, перпендикулярного плоскости циклотронной орбиты электрона.

Вторым условием является соответствие радиуса

правилу квантования круговых орбит электронов (т.е. второму постулату Бора). Использование второго постулата Бора в данном случае необходимо вследствие того, что циклотронные орбиты электронов могут быть устойчивыми только в том случае, когда на длине окружности орбиты укладывается целое число длин волн де Бройля . Покажем, как целое число длин волн де Бройля, укладывающихся на длине окружности орбиты электрона, связано со вторым постулатом Бора.

(17)

(18)

(19)

В формулах (17-19) содержатся следующие обозначения:

– поступательная скорость движения электрона по n-ой циклотронной орбите;

– радиус n-ой циклотронной орбиты.

Приравнивая условия (16) и (19) найдём значение индукции магнитного поля

в данном случае:

(20)

Площадь, охватываемую n - ой циклотронной орбитой электрона, найдём по формуле (21), следующей из (19):

(21)

Поэтому магнитный поток

, создаваемый внешним магнитным полем через площадь, ограниченную n - ой циклотронной орбитой одиночного электрона, находится по формуле:

(22)

В формуле (22) величина

(23)

является квантом магнитного потока.

Это же значение

а, соответственно, и значение

в согласии с (22), можно получить из формулы (16) , из которой следует, что при любом значении

квант магнитного потока, создаваемого внешним магнитным полем через площадь, ограниченную n-ой циклотронной орбитой одиночного электрона, всегда находится по формуле (23).

Теперь представим себе, что металлическое кольцо охладили до низкой температуры и перевели в сверхпроводящее состояние. Затем перпендикулярно плоскости кольца включили внешнее магнитное поле. За некоторый промежуток времени Δt индукция внешнего магнитного поля изменилась от нулевого значения до величины

. Так как магнитная индукция в течение времени Δt является переменной величиной, то сверхпроводящие электроны по закону электромагнитной индукции приобретут ускорение и в течение времени Δt их скорость достигнет некоторого значения

, после достижения индукцией внешнего магнитного поля величины

её изменение прекращается. Поскольку направление силовых линий индукции

внешнего магнитного поля перпендикулярно траектории движения электронов в сверхпроводящем кольце, то под действием силы Лоренца после достижения значения

электроны будут двигаться по циклотронным орбитам некоторых радиусов

, которые находятся в соответствии с записанными выше условиями (16) и (19).

Круговые токи, которые вследствие движения сверхпроводящих электронов появятся в металлическом кольце, создадут магнитное поле с индукцией

, равной по величине и противоположной по направлению индукции

. Поэтому результирующий магнитный поток через площадь, охватываемую внешним контуром кольца, будет равен нулю. Это явление известно как диамагнетизм сверхпроводников
. Итак, явление диамагнетизма сверхпроводников указывает на то, что магнитное поле, создаваемое двигающейся по окружности заряженной частицей, всегда полностью компенсирует внешнее магнитное поле, перпендикулярное к плоскости циклотронной орбиты частицы и вынуждающее эту частицу двигаться по окружностям. Для двигающейся по окружности заряженной частицы при отсутствии внешнего магнитного поля всегда можно подобрать в соответствии с условием (16) внешнее магнитное поле, перпендикулярное плоскости её орбиты, индукция которого будет полностью компенсировать индукцию магнитного поля, создаваемого движущейся по окружности заряженной частицей.

Незатухающий сверхпроводящий ток можно получить и другим способом, отличным от описанного выше. Поместим кольцо из сверхпроводника в перпендикулярное к нему магнитное поле. Охладив затем кольцо ниже критической температуры, выключим поле. В результате в кольце индуцируется незатухающий электрический ток

. В данном случае отсутствует внешнее магнитное поле с индукцией

, однако сверхпроводящие электроны создают собственное магнитное поле с индукцией

, которое может быть измерено. Явление идеального диамагнетизма сверхпроводников указывает на то, что магнитное поле с индукцией

и без наличия внешнего поля с индукцией

имеет те же параметры, как и при наличии поля с индукцией

. Напомню, что поле с индукцией

это такое магнитное поле, силовые линии которого перпендикулярны плоскости циклотронной орбиты электрона и направлены навстречу силовым линиям магнитного поля, создаваемого движущимся электроном, и при этом поле с индукцией

может полностью компенсировать поле с индукцией

. Поэтому формулы, которые используются для расчёта виртуального внешнего поля с индукцией

могут быть использованы и для расчёта собственного магнитного поля электрона с индукцией

.

Вернёмся теперь к атому модели Бора. Зная скорость движения электрона в атоме Бора и радиус его орбиты мы можем рассчитать параметры внешнего магнитного поля, при которых электрон вне атома Бора двигался бы с такой же скоростью и по тому же радиусу, что и в атоме модели Бора. Для такого внешнего магнитного поля мы можем рассчитать величину магнитного потока

через площадь, охваченную орбитой электрона. Явление диамагнетизма сверхпроводников указывает на то, что магнитный поток

, создаваемый в данном случае током электрона вследствие его движения по циклотронной орбите, должен быть равен по модулю магнитному потоку

, отсюда мы можем найти магнитный поток

, создаваемый электроном в атоме модели Бора.

Итак, зная скорость движения электрона по орбите

в атоме Бора и радиус его орбиты

, в соответствии с условием (16) найдём значение индукции

, при которой электрон во внешнем магнитном поле будет двигаться с такой же скоростью

и по тому же радиусу

, как и в атоме модели Бора.

(24)

Используя условие (19), найдём площадь S, охватываемую орбитой электрона

(25)

(Величины

и

в (24) и (25) взяты из ).

Отсюда найдём магнитный поток

, создаваемый внешним магнитным полем

(26)

Вследствие того, что, как показывает явление диамагнетизма сверхпроводников,

, магнитный поток, создаваемый электроном в атоме Бора

равен:

(27)

Итак, магнитный поток в атоме модели Бора, создаваемый одиночным электроном при его движении по круговой орбите, квантуется в соответствии с постоянной

, которая и является квантом магнитного потока. Поэтому справедливы формулы (13), (14) и (15), а формулы (11) и (12) не соответствуют физической реальности.

4. Качественное обоснование величины кванта магнитного потока h/2|e|, создаваемого одиночным электроном

Дадим, дополнительно к приведённому выше в разделе 3, качественное обоснование величины магнитного потока

, создаваемого одиночным электроном, в соответствии с формулами (13), (14) и (15). В связи с этим рассмотрим следующий мысленный эксперимент. Допустим, что электрон, покоящийся в какой-либо инерциальной системе отсчёта (ИСО), под действием приложенной к нему силы F получает ускорение и в результате прямолинейного равноускоренного движения достигает некоторой скорости

, после достижения скорости

равноускоренное движение электрона прекращается и в дальнейшем он движется равномерно и прямолинейно со скоростью

. В соответствии с законом сохранения энергии энергия источника движения электрона, создающего силу F, преобразуется в кинетическую энергию электрона. Так как движение электрически заряженной частицы всегда сопровождается возникновением магнитного поля, то при самом незначительном отклонении состояния электрона от покоя в данной ИСО возникнет магнитное поле электрона, Так как электрон движется с ускорением, то это будет переменное магнитное поле, которое в согласии с первым законом Максвелла в дифференциальной форме создаёт вихревое электрическое поле

(28)

Поле электрических некулоновых сил, вызванное изменением во времени магнитного поля, называют электромагнитным полем. Поэтому можно утверждать, что с началом движения электрона в данной ИСО появляется электромагнитное поле. В электромагнитном поле электрические силы неразрывно связаны с магнитными силами и порождены в любой точке пространства изменением здесь во времени магнитных сил

. В согласии с законом сохранения энергии для создания электромагнитного поля электрона затрачивается энергия источника его движения, поэтому энергия электромагнитного поля электрона по своей величине эквивалентна его кинетической энергии, т.е. кинетическая энергия и электромагнитная энергия в данном случае являются различными формами одного и того же количества энергии, затраченного источником движения на ускоренное движение электрона. Следовательно, запись уравнения (12), а, соответственно, и уравнения (11), не соответствует физической реальности. В уравнении (12) кинетическая энергия приравнивается к энергии магнитного поля, возникшего с началом движения электрона, и не учитывается, что при ускоренном движении электрона в соответствии с формулой (28) появляется вихревое электрическое поле, для создания которого также требуется энергия источника движения электрона. Поэтому уравнение (12) должно быть записано в виде:

(29)

где,

– энергия магнитного поля электрона в рассматриваемом случае;

– энергия электрического вихревого поля электрона в рассматриваемом случае.

Силовые линии напряжённости E вихревого электрического поля направлены по отношению к электрону так, что, в соответствии с правилом Ленца, препятствуют изменению магнитного поля

, т.е. силовые линии напряжённости E направлены против вектора скорости электрона V, а произведение Ee играет в данном случае роль силы инерции электрона. «Сила инерции материальной точки является реальной силой, представляющей собой противодействие материальной точки изменению ее скорости …» . После достижения скорости

и дальнейшего прямолинейного и равномерного движения электрона энергия магнитного поля не изменяется и сохраняется, а вихревое электрическое поле в соответствии с уравнением (28) исчезает, при этом его энергия в согласии с законом сохранения энергии переходит в энергию постоянного электрического поля электрона. Согласно специальной теории относительности (СТО) при движении электрона относительно ИСО происходит сокращение его размеров в направлении движения, причём это сокращение размеров является принципиально наблюдаемым. Как отмечается в : «… мы должны сказать, что лоренцево сокращение не есть свойство одного масштаба, а представляет собой принципиально наблюдаемое взаимное свойство двух движущихся относительно друг друга масштабов», в этом смысле лоренцево сокращение размеров тел в направлении их движения носит объективный характер. Но сокращение размеров электрона в направлении его движения означает и увеличение плотности силовых линий его электрического поля в направлении движения, что эквивалентно увеличению энергии электрического поля электрона за счёт его кинетической энергии, поэтому кинетическая энергия электрона не может быть равна только энергии его магнитного поля и, следовательно, уравнения (11) и (12) неверны.

Как отмечается в

: «… материальная основа магнитного поля, возникающего при движении электрона (а также и электрического поля, связанного с зарядом электрона), неотделима от электрона. При ускорении электрон приобретает дополнительную массу от ускоряющего этот электрон поля, при торможении он отдаёт ранее приобретённую массу тормозящему полю». Приобретение электроном массы при его ускорении и отдача приобретённой им ранее массы происходят в соответствии с законом пропорциональности массы и энергии СТО.

Так как выше в данном разделе было показано, что как при ускорении электрона, так и при дальнейшем его движении с постоянной скоростью кинетическая энергия электрона всегда больше энергии его магнитного поля, то уравнения (11) и (12) не соответствуют физической реальности и поэтому квант магнитного потока, создаваемого одиночным электроном, не может быть равен

. Так как следующим меньшим значением кванта магнитного поля может быть только величина

, то следует признать справедливость формул (13), (14) и (15) для одиночного электрона.

В некоторых источниках (см.

) значение кинетической энергии одиночного электрона приравнивается к энергии создаваемого им магнитного поля (

, формула (12) в данной статье), что, как было показано выше, не соответствует физической реальности. При дальнейшем выводе в получают величину кванта магнитного потока Φ0=h/|e|. Если принять значение кинетической энергии одиночного электрона

(формула (14) в данной статье), то в будет получена величина кванта магнитного потока

.

Итак, из качественного анализа движения одиночного электрона, приведённого в данном разделе статьи, следует, что кинетическая энергия одиночного электрона равна сумме энергий его магнитного и электрического полей, при этом энергия магнитного поля и, появившаяся в результате движения электрона, дополнительная энергия его электрического поля равны между собой (формула (15) в данной статье).

5. Экспериментальное обнаружение квантования магнитного потока в соответствии с константой h/2|e|

Как было отмечено во введении к данной статье, квантование магнитного потока было открыто экспериментально Б. С. Дивером и У. М. Фейрбенком и независимо Р. Доллом и М. Нёбауэром в 1961 году. Эксперимент показал, что квант магнитного потока определяется величиной

. Описание указанных экспериментов можно найти в .

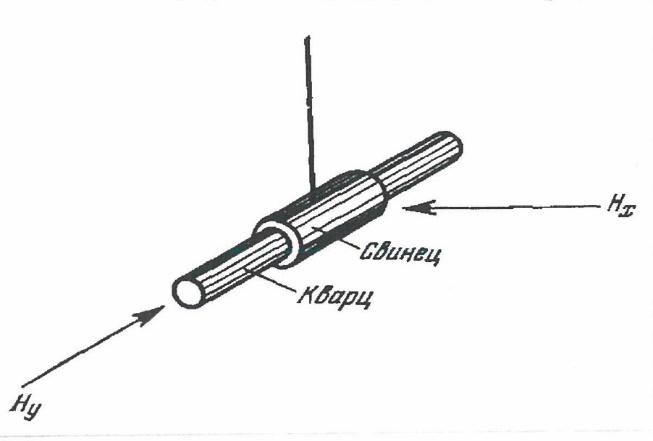
В экспериментах Дивера и Фейрбенка , в качестве сверхпроводящих цилиндров использовались оловянные трубки с внутренним диаметром порядка 1,5 ∙ 10-5 м (15 мкм) и длиной около 10-2 м (10 мм). Опыты Долла и Нёбауэра , проводились на свинцовой трубке диаметром 10-5 м (10 мкм) и длиной 0,6 мм. В опытах Долла и Нёбауэра образец переводился в сверхпроводящее состояние в поле

, параллельном оси цилиндра, после чего поле выключалось (рис.1).

Опыты Долла и Нёбауэра

Сверхпроводящий ток, возникающий в момент выключения поля, создаёт магнитный поток через внутреннюю полость цилиндра, который можно измерить. В опытах Дивера и Фейрбенка индуцирование сверхпроводящего тока также осуществлялось при выключении исходного поля, параллельного оси цилиндра. Было установлено, что поток через цилиндр увеличивается ступенчато с увеличением напряженности исходного приложенного поля.

На рис. 2 приведены результаты Долла и Нёбауэра, на рис.3 - Дивера и Фейрбенка .

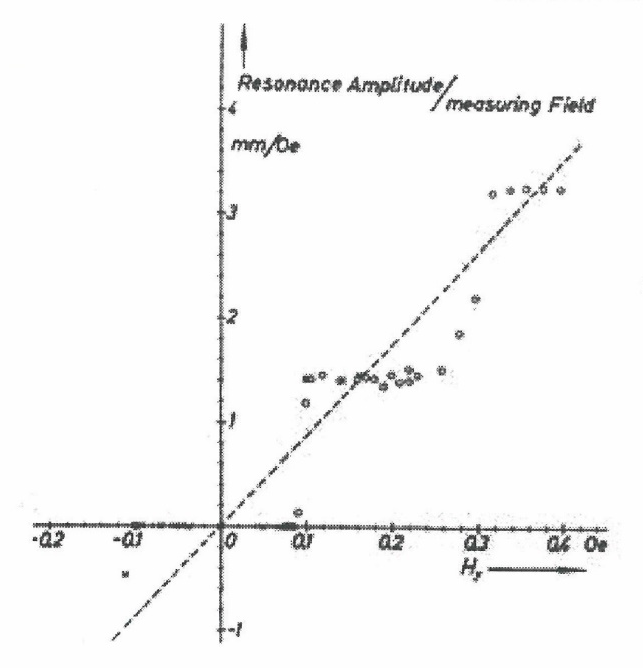
Результаты Р. Долла и М. Нёбауэра

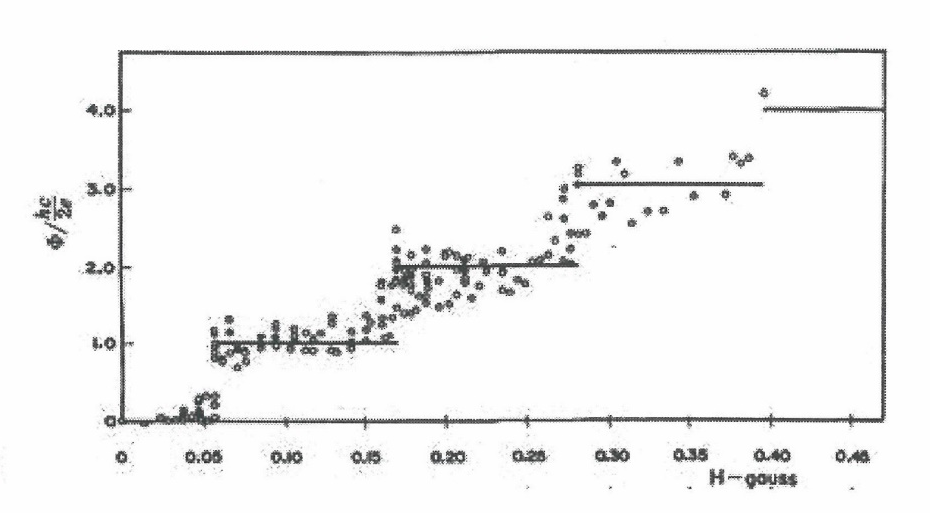
Результаты Б.С. Дивера и У.М. Фейрбенка

В сверхпроводящих трубках имеется очень большое количество сверхпроводящих электронов . Так как радиус трубок является фиксированной величиной и толщины их стенок недостаточно для того, чтобы в стенках трубок уместились в радиальном направлении две круговые орбиты (как это будет показано ниже), то каждый отдельный сверхпроводящий электрон в согласии с условиями (16) и (19) будет двигаться по отдельной круговой орбите с одинаковым для всех электронов радиусом и одинаковой скоростью вокруг общей оси, при этом плоскости каждой орбиты параллельны друг другу. Все электроны в результате своего кругового движения будут создавать некоторое магнитное поле с индукцией

, которое принципиально в силу свойства диамагнетизма сверхпроводников может быть скомпенсировано некоторым внешним магнитным полем с индукцией

, которая в согласии с соотношением (16) может быть рассчитана по формуле

(30)

где

– количество сверхпроводящих электронов.

Так как величина

в (30) сокращается, то оказывается, что индукция магнитного поля внутри сверхпроводящих трубок

в рассматриваемых опытах имеет такое же значение, какое необходимо и для вращения по циклотронной орбите с такими же параметрами одного электрона, соответственно и магнитный поток

, создаваемый во внутренней полости сверхпроводящих трубочек всеми сверхпроводящими электронами эквивалентен магнитному потоку, создаваемому одним электроном, поэтому и длина трубок в экспериментах Дивера и Фейрбенка, Долла и Нёбауэра (10 мм и 0,6 мм) не влияет на величину магнитного потока и кванта магнитного потока, обнаруженных в названых экспериментах. Возможно, что это удивительное явление имеет квантовое объяснение. Так как все электроны в сверхпроводящих трубках, двигаясь по индивидуальным круговым орбитам, находятся в одинаковом квантовом состоянии (как это будет показано ниже), то в силу принципа Паули их квантовые состояния в объёме сверхпроводника не могут накладываться друг на друга, соответственно и магнитные потоки, создаваемые каждым отдельным электроном вдоль оси сверхпроводника не пересекаются между собой и поэтому не складываются, а магнитный поток в каждом сечении полости трубки, перпендикулярном её оси, равен магнитному потоку, создаваемому одним электроном.

Используя условия (19) и (16) запишем формулу для нахождения радиуса циклотронной орбиты одного электрона в опытах Дивера и Фейрбенка, Долла и Нёбауэра:

(31)

(Формула (31) совпадает с формулой (10) в

).

В формуле (31)

это индукция в данном случае виртуального подобранного внешнего магнитного поля, перпендикулярного орбите электрона, при которой электрон двигался бы со скоростью

по циклотронной орбите с радиусом

, по которой он движется в действительности после отключения исходного внешнего поля в названых экспериментах. Так как, как было отмечено ранее, вследствие диамагнетизма сверхпроводников

, то формулу (31) запишем в виде

(32)

Подставив в формулу (32) Bown = 0,1 гс (10-5Тл) согласно эксперименту Дивера и Фейрбенка

и Bown = 0,25 гс (2,5∙10-5Тл) согласно эксперименту Долла и Нёбауэра при

вычислим соответствующие радиусы круговых орбит в названных экспериментах. Принимаем

, так в указано, что измеренные значения магнитного потока

равны кванту магнитного потока

при значениях магнитной индукции Bown = 0,1 гс (10-5Тл) и Bown = 0,25 гс (2,5∙10-5Тл). Для опыта Дивера и Фейрбенка мы получим значение rnc = 0,812∙10-5м (8,12 мкм), а для опыта Долла и Нёбауэра rnc = 0,513∙10-5м (5,13 мкм), эти значения rnc с высокой степенью точности соответствуют значениям внутренних диаметров сверхпроводящих цилиндров, приведённых в . Как известно, сверхпроводящий ток течёт в поверхностном слое сверхпроводящего цилиндра толщиной порядка λ ∼600 Å (0,06 мкм) , поэтому сравнение значений rnc, полученных с помощью формулы (32), со значениями внутренних диаметров сверхпроводящих трубок, приведёнными в , позволяет с некоторым приближением (из-за размера λ) вычислить толщину стенок трубок в рассматриваемых экспериментах. В опытах Дивера и Фейрбенка, согласно приведённым расчётам, толщина стенки оловянной трубки составляет величину порядка 0,6 мкм, в опытах Долла и Нёбауэра толщина напылённого слоя свинца составляет величину порядка 0,13 мкм. Очевидно, что при такой толщине стенок сверхпроводящих трубочек в радиальном направлении может уместиться только одна круговая орбита. Итак, расчётные формулы для радиусов круговых орбит электронов, полученные с использованием условий (16) и (19) для одиночных электронов, с высокой степенью точности соответствуют экспериментальным значениям диаметров сверхпроводящих трубок, указанных в .

Как было показано в разделе 3 данной статьи, использование условий (16) и (19) для одиночного электрона всегда приводит к значению кванта магнитного потока

(как и применение формулы (16) в ), величина кванта магнитного потока

и была обнаружена в рассматриваемых в данном разделе статьи опытах Дивера и Фейрбенка, Долла и Нёбауэра.

В

приведена формула (21) для длины волны

одиночного электрона, двигающегося под влиянием внешнего, перпендикулярного плоскости его циклотронной орбиты, магнитного поля с индукцией B. В рассматриваемом случае индукцию B вследствие свойства диамагнетизма сверхпроводников можно записать как

и соответственно формулу (21) из запишем в виде

(33)

Расчёт

при

и значениях

, приведённых в (0,1гс и 0,25гс), даёт величину

в опытах Дивера и Фейрбенка и величину

в опытах Долла и Нёбауэра, что очень хорошо соответствует значениям диаметров сверхпроводящих трубок в рассматриваемых экспериментах, на длинах окружностей орбит электронов при

укладывается одна длина волны де Бройля. Точность формулы (33), следующей из формулы (21) из , указывает и на правильность формулы (16) в (так как эти формулы взаимно связаны), а из формулы (16) следует, что квант магнитного потока при переходе электрона с одной циклотронной орбиты на другую всегда определяется величиной

.

Для того чтобы электронам перейти на следующий энергетический уровень при фиксированном диаметре сверхпроводящих трубок, необходимо уменьшить в 2 раза длину волны де Бройля электронов, тогда на тех же длинах орбит электронов будет укладываться две длины волны де Бройля, что соответствует квантовому числу

. Из формулы де Бройля (17) следует, что для этого необходимо увеличить циклотронную скорость электронов

в 2 раза. Добиться этого можно при помощи увеличения напряжённости H исходного магнитного поля (см. рис. 2 и рис.3). Из условия (19) следует, что при

изменению квантового числа

на единицу соответствует ступенчатое изменение скорости электронов с

до

. До тех пор, пока напряжённость H исходного магнитного поля не примет такое значение, при котором возможно достижение электронами скорости

, квантовый переход с числа n = 1 на число n = 2 невозможен и скорость электронов до названого квантового перехода будет оставаться

. Вследствие этого имеется определённый диапазон изменения напряжённости H исходного поля, при котором скорость электронов

остаётся постоянной и, соответственно, остаются постоянными значения величин магнитной индукции

и магнитного потока

, создаваемых сверхпроводящими электронами, поэтому на рис. 2 и рис.3 наблюдаются плато величин магнитного потока.

Из формулы (33) следует, что уменьшению длины волны де Бройля электронов в 2 раза и изменению квантового числа

с 1 до 2 соответствует и ступенчатое увеличение индукции магнитного поля

в 2 раза, что при фиксированных диаметрах сверхпроводящих трубочек приводит к ступенчатому повышению величины магнитного потока с

до

, именно это и наблюдалось в экспериментах. В дальнейшем при повышении напряжённости H исходного магнитного поля и последующим ступенчатом повышении скоростей орбитального движения сверхпроводящих электронов до величин

,

и т.д. происходит изменение величины магнитного потока

внутри сверхпроводящих трубок в соответствии с формулой

(34)

Формула (34) совпадает с формулами (22), (26), (27), полученными в данной статье для одного электрона.

Следует отметить, что в современной научной литературе, в которой рассматривается квантование магнитного потока, авторы вносят заряд

в исходные формулы для вывода величины кванта магнитного потока и затем получают результат, соответствующий эксперименту (см., например, ). В данной работе показано, что для объяснения квантования магнитного потока в сверхпроводящем цилиндре в соответствии с константой (квантом)

нет необходимости прибегать к концепции куперовской пары электронов.

6. Основные результаты

1. Вывод из формулы де Бройля основных уравнений (6) и (7) для заряженных частиц, двигающихся по окружности, согласно данным автора статьи, является новым, т.е. ранее не известным. Сами уравнения (6) и (7) также являются новыми.

2. С использованием свойства диамагнетизма сверхпроводников предложен новый метод расчёта магнитных полей, создаваемых двигающимися по окружности одиночными электронами. Вначале применяются условия (16) и (19) и производится расчёт виртуального внешнего магнитного поля, перпендикулярного орбите электрона, которое может полностью скомпенсировать магнитное поле, создаваемое действительно двигающимся электроном, а затем результаты расчёта применяются к действительно существующему магнитному полю, создаваемому двигающимся электроном. Именно так в данной статье были рассчитаны параметры магнитного поля, создаваемого одиночным электроном, в атоме модели Бора.

3. С использованием нового метода расчёта магнитного поля (см. п. 2 основных результатов) обосновано положение о том, что квантование магнитного потока одиночных электронов, двигающихся по окружностям как в атоме модели Бора (формулы 9 и 27), так и в сверхпроводящем кольце происходит пропорционально номеру

энергетического уровня электрона в соответствии с константой

, при этом величина

является квантом магнитного потока. Этот результат является новым, так как получен для одного электрона без использования концепции куперовской пары электронов.

4. В статье обосновано положение о том, что величина энергии магнитного поля электрона в рассмотренных случаях всегда равна половине энергии уровня электрона или половине кинетической энергии электрона, двигающегося по круговой орбите (формула 15). Этот новый результат следует из основных формул (6) и (7), строго выведенных из формулы де Бройля.

5. В статье с использованием условий (16) и (19) выполнен расчёт диаметров и толщин стенок сверхпроводящих трубок в экспериментах Дивера и Фейрбенка, Долла и Нёбауэра, что указывает на правильность следующих из условий (16) и (19) формул для расчёта магнитных полей электронов, двигающихся по циклотронным орбитам. Показано, что индукция магнитного поля и магнитный поток, создаваемые всей совокупностью сверхпроводящих электронов эквивалентны магнитной индукции и магнитному потоку, создаваемому одним сверхпроводящим электроном. Эти результаты являются новыми.

7. Заключение

В результате проведённого исследования установлено, что квантование магнитного потока в атоме модели Бора (формулы 6-9, 24-27), в сверхпроводящем кольце (формулы 22 и 26) и в сверхпроводящем цилиндре (формула 34) должно происходить в согласии с константой

при учёте заряда только одного электрона, т.е. результаты данной статьи не согласуются с концепцией куперовских пар электронов.

Возможность квантования магнитного потока в соответствии с константой

при учёте заряда только одного электрона делает возможным поиск альтернативных вариантов объяснения явления сверхпроводимости.

Additional materials

Not specified

Financing

The authors did not receive financial support for research, writing and publishing articles

Acknowledgements

Not specified

Conflicts of interests

Not specified

References

London F. On the Problem of the Molecular Theory of Superconductivity / F. London // Phys. Rev. — 1948. — Vol.74. — № 5. — P. 562-573.

London F. Superfluids. Vol.1.: Macroscopic Theory of Superconductivity / F. London. — N.Y.: John Wyley&Sons, 1950. — P. 151-152.

Tomilin K.A. K istorii otkrytija kvantovanija magnitnogo potoka [To the History of the Discovery of Magnetic Flux Quantization] / K.A. Tomilin. — Annual Scientific Conference of IIET RAS, 2004. [in Russian]

Glazkov V.N. Jelektrodinamika sverhprovodnikov. Osnovy mikroskopiki. Sverhprovodniki II roda (zametki k lekcijam po obshhej fizike), lekcija 9 [Electrodynamics of Superconductors. Fundamentals of Microscopy. Superconductors of II kind (notes for lectures on general physics), lecture 9] / V.N. Glazkov. — M.: MFTI, 2017. [in Russian]

Prohorov A.M. Bol'shoj jenciklopedicheskij slovar'. Fizika [Big Encyclopaedic Dictionary. Physics] / A.M. Prohorov [et al.] — M.: Great Russian Encyclopaedia, 1998. [in Russian]

Sokolov S.A. Novoe v oblasti sverhprovodimosti i perspektivy [New developments in the field of superconductivity and prospects] / S.A. Sokolov // T – comm – Telecommunications and Transport. — 2010. — № 8. — P. 10-12. [in Russian]

Bom. D. Kvantovaja teorija [Quantum Theory] / D. Bom. — M.: Nauka, 1965. [in Russian]

Putilov K.A. Kurs fiziki, tom 3 [Course of Physics, volume 3] / K.A. Putilov, V.A. Fabrikant. — M.: GI FML, 1963. [in Russian]

Aslamazov L.G. Udivitel'naja fizika [Fascinating Physics] / L.G. Aslamazov, A.A. Varlamov. — M.: Nauka, 1987. [in Russian]

Glazkov V.N. Nizkorazmernye jelektronnye sistemy (zametki k lekcijam po obshhej fizike), lekcija 12 [Low-dimensional Electronic Systems (notes for lectures on general physics), lecture 12] / V.N. Glazkov. — M.: MFTI, 2016. [in Russian]

Abrikosov A.A. Osnovy teorii metallov [Fundamentals of Metal Theory] / A.A. Abrikosov. — M.: Fizmatlit, 2010. [in Russian]

Javorskij B.M. Spravochnik po fizike [Physics guide] / B.M. Javorskij, A.A. Detlaf. — M.: Nauka, 1979. [in Russian]

Izbreht A.R. Jenergeticheskie urovni jelektronov v magnitnom pole i celochislennyj kvantovyj jeffekt Holla [Energy Levels of Electrons in a Magnetic Field and the Integer Quantum Hall Effect] / A.R. Izbreht // Mezhdunarodnyj nauchno-issledovatel'skij zhurnal [International Research Journal]. — 2023. — № 3 (129). [in Russian]

Savel'ev I.V. Kurs obshhej fiziki, tom 3 [Course in General Physics, Volume 3] / I.V. Savel'ev. — M.: Nauka, 1987. [in Russian]

Putilov K.A. Kurs fiziki, tom 2 [Course in Physics, Volume 2] / K. A. Putilov. — M.: GI FML, 1963. [in Russian]

Jablonskij A.A. Kurs teoreticheskoj mehaniki [Theoretical Mechanics Course] / A.A. Jablonskij, V.M. Nikiforova. — SPb.: Lan', 2001. [in Russian]

Pauli V. Teorija otnositel'nosti [Theory of Relativity] / V. Pauli. — M.: Nauka, 1991. [in Russian]

Pitaevskij L.P. Makroskopicheskie kvantovye javlenija [Macroscopic Quantum Phenomena] / L.P. Pitaevskij // UFN. — 1966. — Vol. 90. — Iss. 4 [in Russian]

Dеаνег В.S. Experimental Evidence for Quantized Flux in Superconducting Cylinders / В.S. Dеаνег, W.М. Fairbank // Phys. Rev. Letts. — 1961. — 7(43).

Dоll R. Experimental Proof of Magnetic Flux Quantization in a Superconducting Ring / R. Dоll, Μ. Näbaueге // Phys. Rev. Letts. — 1961. — 7(51).

Kurin V.V. Fizika sverhprovodnikov. Vvodnyj kurs [Physics of Superconductors. Introductory course] / V.V. Kurin. — Nizhnij Novgorod: Institute of Physics of Microstructures RAS, 2004. [in Russian]

References

London F. On the Problem of the Molecular Theory of Superconductivity / F. London // Phys. Rev. — 1948. — Vol.74. — № 5. — P. 562-573.
London F. Superfluids. Vol.1.: Macroscopic Theory of Superconductivity / F. London. — N.Y.: John Wyley&Sons, 1950. — P. 151-152.
Tomilin K.A. K istorii otkrytija kvantovanija magnitnogo potoka [To the History of the Discovery of Magnetic Flux Quantization] / K.A. Tomilin. — Annual Scientific Conference of IIET RAS, 2004. [in Russian]
Glazkov V.N. Jelektrodinamika sverhprovodnikov. Osnovy mikroskopiki. Sverhprovodniki II roda (zametki k lekcijam po obshhej fizike), lekcija 9 [Electrodynamics of Superconductors. Fundamentals of Microscopy. Superconductors of II kind (notes for lectures on general physics), lecture 9] / V.N. Glazkov. — M.: MFTI, 2017. [in Russian]
Prohorov A.M. Bol'shoj jenciklopedicheskij slovar'. Fizika [Big Encyclopaedic Dictionary. Physics] / A.M. Prohorov [et al.] — M.: Great Russian Encyclopaedia, 1998. [in Russian]
Sokolov S.A. Novoe v oblasti sverhprovodimosti i perspektivy [New developments in the field of superconductivity and prospects] / S.A. Sokolov // T – comm – Telecommunications and Transport. — 2010. — № 8. — P. 10-12. [in Russian]
Bom. D. Kvantovaja teorija [Quantum Theory] / D. Bom. — M.: Nauka, 1965. [in Russian]
Putilov K.A. Kurs fiziki, tom 3 [Course of Physics, volume 3] / K.A. Putilov, V.A. Fabrikant. — M.: GI FML, 1963. [in Russian]
Aslamazov L.G. Udivitel'naja fizika [Fascinating Physics] / L.G. Aslamazov, A.A. Varlamov. — M.: Nauka, 1987. [in Russian]
Glazkov V.N. Nizkorazmernye jelektronnye sistemy (zametki k lekcijam po obshhej fizike), lekcija 12 [Low-dimensional Electronic Systems (notes for lectures on general physics), lecture 12] / V.N. Glazkov. — M.: MFTI, 2016. [in Russian]
Abrikosov A.A. Osnovy teorii metallov [Fundamentals of Metal Theory] / A.A. Abrikosov. — M.: Fizmatlit, 2010. [in Russian]
Javorskij B.M. Spravochnik po fizike [Physics guide] / B.M. Javorskij, A.A. Detlaf. — M.: Nauka, 1979. [in Russian]
Izbreht A.R. Jenergeticheskie urovni jelektronov v magnitnom pole i celochislennyj kvantovyj jeffekt Holla [Energy Levels of Electrons in a Magnetic Field and the Integer Quantum Hall Effect] / A.R. Izbreht // Mezhdunarodnyj nauchno-issledovatel'skij zhurnal [International Research Journal]. — 2023. — № 3 (129). [in Russian]
Savel'ev I.V. Kurs obshhej fiziki, tom 3 [Course in General Physics, Volume 3] / I.V. Savel'ev. — M.: Nauka, 1987. [in Russian]
Putilov K.A. Kurs fiziki, tom 2 [Course in Physics, Volume 2] / K. A. Putilov. — M.: GI FML, 1963. [in Russian]
Jablonskij A.A. Kurs teoreticheskoj mehaniki [Theoretical Mechanics Course] / A.A. Jablonskij, V.M. Nikiforova. — SPb.: Lan', 2001. [in Russian]
Pauli V. Teorija otnositel'nosti [Theory of Relativity] / V. Pauli. — M.: Nauka, 1991. [in Russian]
Pitaevskij L.P. Makroskopicheskie kvantovye javlenija [Macroscopic Quantum Phenomena] / L.P. Pitaevskij // UFN. — 1966. — Vol. 90. — Iss. 4 [in Russian]
Dеаνег В.S. Experimental Evidence for Quantized Flux in Superconducting Cylinders / В.S. Dеаνег, W.М. Fairbank // Phys. Rev. Letts. — 1961. — 7(43).
Dоll R. Experimental Proof of Magnetic Flux Quantization in a Superconducting Ring / R. Dоll, Μ. Näbaueге // Phys. Rev. Letts. — 1961. — 7(51).
Kurin V.V. Fizika sverhprovodnikov. Vvodnyj kurs [Physics of Superconductors. Introductory course] / V.V. Kurin. — Nizhnij Novgorod: Institute of Physics of Microstructures RAS, 2004. [in Russian]

Review

All articles are peer-reviewed. But the reviewer or the author of the article chose not to publish a review of this article in the public domain. The review can be provided to the competent authorities upon request.

Author information

ORCID:0000-0001-8018-1144
AffiliationRetired, Ekaterinburg, Russian Federation
Role:Author
ELIBRARY AUTHOR ID:941401

Article metrics

Downloads:29

ViewsDownloads

Views

Total: