PREDICTION OF QUANTOMOBILE STABILITY WITH TEST MATERIALS OF REFERENCE AERODYNAMIC MODELS OF AUTOMOBILES
PREDICTION OF QUANTOMOBILE STABILITY WITH TEST MATERIALS OF REFERENCE AERODYNAMIC MODELS OF AUTOMOBILES
Abstract
The aim of the study was to predict the stability of a quantum car (a vehicle with a quantum motor (QM)) using the materials of tests of reference aerodynamic models of automobiles based on high-drag bodies (HDBs). The methods include: examination of the force balance of the quantomobile, the balance of force moments; taking into account the features of the air impact forces; adaptation of the HDBs test results to the modelling of the quantomobile. The author's Simulink model of the ground motion of the quantomobile (MPDC) is modernized, taking into account the target settings. A piecewise linear representation of the dynamics of the aerodynamic coefficients' variation under changing Reynolds number Re and body velocity V is generated. The main stability estimators were the values of the longitudinal overturning moment. The results of calculations carried out on the basis of weight and geometric data on the prototype KamAZ-5326 vehicle, as well as opposition HDBs 1-Box and Davis, cover a series of acceleration and steady-state motion of micro- and macromodels of quantum cars. Varying parameters: trust magnitude, altitude coordinate of the point of trust application to the crew body, drag coefficient of the supporting wheels, aerodynamic influence coefficients. A set of graphs characterizing the dependence of estimated indicators on the named parameters in the process of implementation of a set of driving modes is presented. The results of the calculations allowed to evaluate the dynamics of occurrence and changes in longitudinal overturning pitching moments and moments required for crew stabilization. Conclusions. The longitudinal unbalance of a quantomobile is different from that of a motor vehicle. Suspension of the trust over the supporting surface results in pitching moments that manifest themselves differently under different conditions. The choice of oppositional HDBs allowed to estimate the values of stability indices as boundary values. To neutralize the overturning moments, additional tracers and/or special aerodynamic aids are required, covered by a single control system with the main FC. The S-model can serve as an operational solver of the engagement of structural stabilizing elements on board the quantomobile. The novelty of the work can be regarded as significant, due to the lack of information on similar conceptual studies of a hypothetical quantomobile.
1. Введение
В последние десятилетия в физике развиваются идеи извлечения энергии из физического вакуума (ФВ) , , , , . На базе этих идей рассматриваются концепции квантовых двигателей (КД), способных найти применение на транспорте , , . Имеются сведения о лабораторных образцах КД , . Предположение, что усилия физиков и инженеров завершатся успешным извлечением энергии ФВ посредством работоспособных конструкций КД, инициирует необходимость рассмотрения особенностей использования траста КД для движения транспортного средства (ТС).
Основная функциональная особенность ТС с КД заключается в том, что КД, создавая направленный траст, способен обеспечить ТС тяговой силой, прикладываемой непосредственно к корпусу экипажа, исключая этим необходимость трансмиссии. Это подобно воздействию на экипаж ракетного двигателя (РД), однако в отличие от РД (где траст создается как реакция на импульс отбрасываемой массы газов), КД создает траст за счет деформации поля ФВ, обеспечивая опору трасту во внешней части задействованного фрагмента поля ФВ , , . Функция рабочей камеры КД заключается в создании деформации пространства-времени , обеспечивающего за счет появляющегося градиента сил возникновение направленного траста . При этом траст, благодаря отсутствию продуктов горения в его тыльной части, получит конструктивную возможность шарнирного обметания пространства с фиксацией любых пространственных углов. Отличием КД от РД явится также отсутствие необходимости содержания на борту запаса топлива.
Квантовый Двигатель является одновременно и Движителем, что может служить основанием введения для всей силовой установки ТС с КД аббревиатуры КДД (Квантовый Двигатель–Движитель). Автором в ряде работ рассмотрены концепции функционирования КДД. Для ТС с КДД введен термин квантомобиль , рассмотрены возможные режимы движения квантомобиля , , , сформированы концептуальные основы теории квантомобиля , , рассмотрена возможность создания всесредного мультимодального квантомобиля (ВМК) , , .
Изъятие трансмиссии из конструкции ТС, при наличии КДД, высвобождает колеса экипажа от функции движителя, они остаются лишь опорными. Вывешенный над опорной поверхностью (ОП) траст меняет схему сил и моментов, используемую для классического автомобиля. Точки возникновения сил тяги в пятнах контакта ведущих колес автомобилей переносятся и трансформируются в точки приложения вектора тяги КД к корпусу ТС , . При наличии возможности обеспечения наклона вектора траста появляется возможность вывешивания экипажа (лифт), либо его прижимания к ОП (антилифт). При всём этом заостряется проблема продольной устойчивости , .
Разница в величинах вертикальных нагрузок на колеса экипажа, с точки зрения продольной устойчивости, для автомобиля в большинстве случаев имеет второстепенное значение – поскольку при движении автомобиля названые нагрузки отражаются реакциями твердой ОП. В случае квантомобиля, однако, во-первых, из-за отсутствия ограничений по сцеплению колес с ОП возможна реализация тяговой силы, значительно превосходящей допустимую для автомобиля. Во-вторых, траст, вывешенный над ОП, формирует составляющую опрокидывающего момента, отсутствующую в автомобильном варианте. В-третьих, в отсутствие твердой опоры вывешенный квантомобиль получит склонность к вращательному движению в плоскости тангажа .
В последнее время в практике исследования аэродинамики автомобиля сложился методологический подход, основой которого является идея покрытия множества реальных форм экипажей некоторой совокупностью упрощенных плохообтекаемых тел (ПОТ) (Simplified bluff body , , , , ), каждое из которых представляет тот или иной класс ТС. Усилия научных коллективов концентрируются на исследованиях аэродинамики разномасштабных моделей этих упрощенных тел, внося вклад в общий прогресс этой области науки и техники. Отметим некоторые из утвердившихся ПОТ: 1-Box , , 2-Box , , Ahmed , Windsor , Docton , Davis , и др. Накопленный таким образом материал позволяет исследователям оценивать аэродинамические характеристики перспективных моделей автомобилей, близких по геометрическим пропорциям и профилю к тому или иному ПОТ. Получаемые оценки служат выработке рекомендаций и решений по обводам корпусов, жесткому и выдвигаемому оперению экипажей, реализации оптимальных режимов движения .
В русле затронутого подхода велика роль масштабирования. Разномасштабность моделей требует привлечения (в качестве критерия адекватности условий моделирования) чисел Рейнолдса , , , (возможно, и чисел Маха и Строхаля – для высоких скоростей), на базе которых определяются скоростные режимы как натурных испытаний, так и расчетных моделей автомобилей. Изложенный подход привлекателен и для построения аэродинамических портретов гипотетических ТС с КДД.
Следует отметить, что гибридное получение аэродинамических показателей на базе экспериментального и алгоритмического разнообразия: испытаний полнонатурных и масштабных моделей, конструктивного различия стендов, способов моделирования дорожного сопротивления, математических и цифровых моделей, практики и качества обработки данных, прочее , – не может предъявлять высоких требований к точности прогнозных оценок для таких гипотетических объектов, как квантомобиль. Тем не менее считаем, что исследование в методическом ключе будет оправданным.
Гипотезой исследования считаем, что разница показателей продольной устойчивости не только между различными конфигурациями квантомобилей, но и между квантомобилями и их автомобилями-аналогами, будет существенной.
Данная статья, являясь логическим продолжением публикации , отражает углубление представлений о продольной устойчивости квантомобиля на базе названых методов с использованием ПОТ.
2. Методы и принципы исследования
2.1. Цель и задачи исследования
Целью исследования обозначили прогнозирование продольной устойчивости квантомобиля с привлечением материалов испытаний ПОТ автомобилей.
Устранение трансмиссии, перенос движительных функций с опорных колес на траст КД, способность вектора траста действовать в плоскости тангажа, – всё это, в отсутствие признанных теоретических основ движения квантомобиля и эмпирических данных, вызывает необходимость использовать подход с опорой на программное имитационное моделирование (ПИМ).
Задачами по достижению цели являются:
1) формирование математической модели продольного движения квантомобиля (МПДК) под поставленную цель;
2) построение Simulink-модели движения квантомобиля – с детализацией скоростных аэродинамических характеристик, с охватом имитации стендовых аэродинамических испытаний и дорожного движения; с отработкой интерфейса взаимодействия с моделью и вывода данных;
3) на базе Simulink-модели проведение ряда ПИМ, покрывающего некоторое множество конфигураций кузова квантомобиля и вариантов его движения;
4) обсуждение и обобщение результатов расчетов;
5) формирование рекомендаций и выводов.
2.2. Вектор траста и особенности его использования в МПДК
Несмотря на имеющиеся публикации автора по концепциям механики ТС с КДД , , , , , ниже для усиления самодостаточности восприятия статьи приведем исходные позиции МПДК.
В рамках продольного движения экипажа в плоскости развёртывания угла тангажа β вектор траста FT раскладывается на две ортогональные компоненты FTx и FTz :
Ограничимся приземным (без отлета) движением квантомобиля по горизонтальной ОП (0 ≤ FTz +Fwz≤ Gq, где Fwz – аэродинамическая подъемная сила, а Gq – вес экипажа). Освободимся от учета динамики вертикальных перемещений ТС. Будем рассматривать непосредственное приложение силы FT к корпусу экипажа в его заданной конструктивной точке.
В данной статье будем рассматривать только лишь горизонтальный вариант реализации траста КД – ради прозрачности использования материалов испытаний ПОТ (способных генерировать и свой лифт, и антилифт).
2.3. Баланс сил и силовых моментов квантомобиля
Используем уравнение баланса горизонтальных сил квантомобиля , , :
где FTx – продольная сила тяги КД (траст), Н;
Fr – сила сопротивления качению ведомых опорных колес, Н;
Fwx – сила сопротивления воздуха продольному движению (drag), Н;
Fa – сила инерции, противодействующая ускорению экипажа, Н;
Gq' – сила давления экипажа на ОП с учетом общего лифта, Н;
fk0 – коэффициент сопротивления качению колес при нулевой скорости;
fkv – скоростной коэффициент сопротивления качению колес, с2/м2;
Vq – текущая скорость продольного движения экипажа, м/с;
cd – коэффициент аэродинамического сопротивления, безразмерный;
ρw – плотность воздуха, Н ×с2/м4;
Sfr – лобовая площадь экипажа, м2;
Gq – исходный вес (сила тяжести) квантомобиля (в отсутствие лифта/антилифта), Н;
g – ускорение свободного падения, м/с2;
a – продольное ускорение экипажа, м/с2;
δwh (deltaWh) – коэффициент инерции вращения опорных колес экипажа.
Поясняем: Gq' = Gq – FTz – Fwz; приведенная масса m’ = Gq(1+δwh)/g в отсутствие трансмиссии учитывает только вращение опорных колес; Fr = Fk0 + Fkv, где Fk0 = fk0 · Gq', а Fkv = fk0 · fkv ·Vq2· Gq'.
График прикладываемых к экипажу сил отображен на рис. 1. (выполненном с привлечением формы кузова Davis , , ). Обозначены: Vq – вектор скорости движения квантомобиля; V∞ – скорость невозмущенного набегающего потока воздуха (|V| = |V∞|); Cg – центр тяжести (ЦТ) экипажа; Gq – сила тяжести экипажа; Fa – приведенная сила инерции экипажа; CFT – точка приложения траста КД к корпусу экипажа; FT, FTx и FTz – сила тяги КД (траст) и ее покоординатные компоненты; Cw – центр давления (ЦД) аэродинамических сил; Fw, Fwx и Fwz – сила воздействия воздуха и ее покоординатные компоненты; Ff1 и Ff2 – силы сопротивления качению передних и задних колес, соответственно; Tf1 и Tf2 – моменты сопротивления качению колес; hFwx, hFTx, hg – расстояния векторов соответствующих сил Fwx, FTx, Fa от ОП; lFwz, lFTz – расстояния векторов соответствующих сил Fwz, FTz до вертикали от оси задних колес; l0 – расстояние вектора силы Fwz до вертикали центра колесной базы; Lwb, L1 и L2 – расстояния базовое и от осей колес до проекции центра тяжести на ОП; A и B – центральные точки пятен контакта колес с ОП; Rz1 и Rz2 – нормальные реакции ОП.
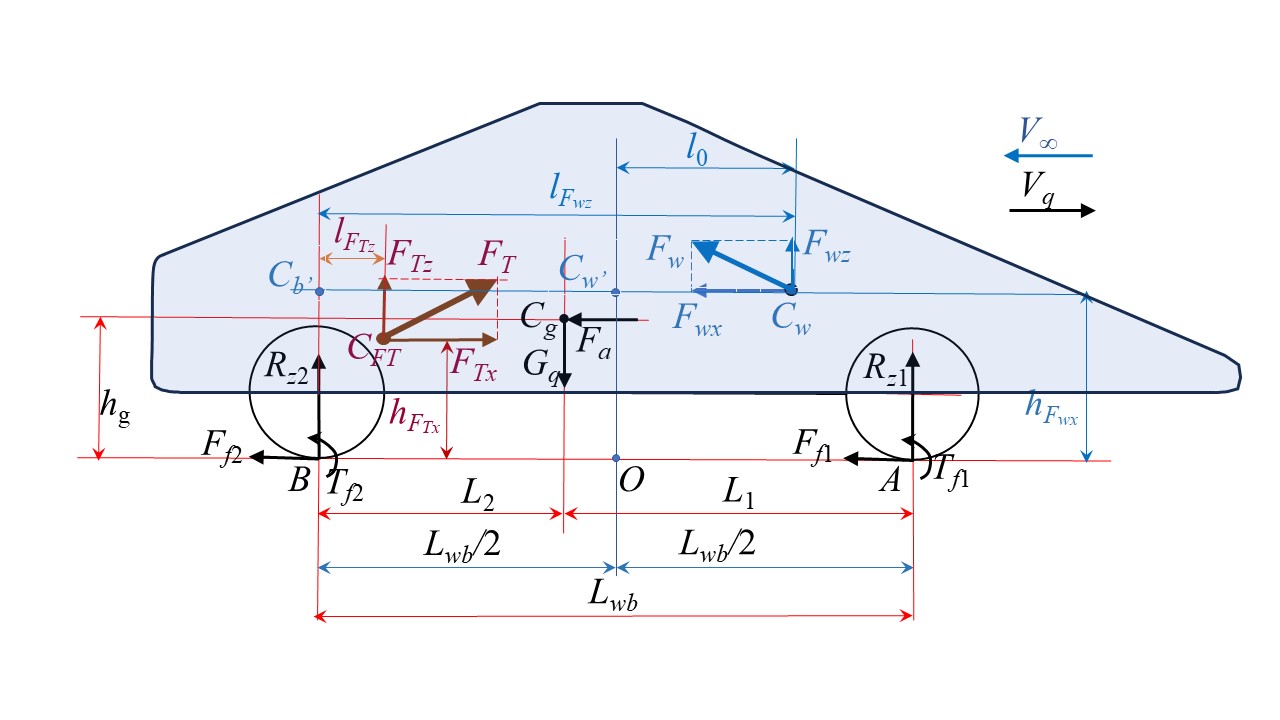
Рисунок 1 - Схема сил, действующих на квантомобиль
Примечание: форма кузова – Davis; по ист. [22], [25], [26]
Если начало связанной плоской системы координат разместить в точке B (назовем её СКB – c осью x по направлению к передку экипажа, осью z вверх; положительными моментами – против часовой стрелки), то сумма всех моментов относительно точки B (см. рис. 1):
Отсюда можно найти нормальную реакцию ОП Rz1.
Аналогичное уравнение моментов относительно точки A позволяет найти реакцию Rz2. Опрокидывающий питч-момент MΣpm = Lwb(Rz1–Rz2)/2. А требуемый стабилизирующий момент (ТСМ) тогда равен Mst = –MΣpm. Для оценки значимости аэродинамического питч-момента (АПМ) MFw = MFwx+MFwz относительно ТСМ Mst введен коэффициент KMFw.Mst = MFw/Mst.
2.4. Учет в МПДК формы представления результатов стендовых аэродинамических испытаний моделей автомобилей
Необходимо было обеспечить в МПДК, с одной стороны, возможность моделирования силового баланса и дорожного движения экипажа в принятой СКB. А с другой стороны, – обеспечить прием коэффициентов аэродинамического воздействия ci (cd, cl, cm), опирающихся на CКO (с началом в срединной точке O рис. 1), а также возможность имитационного моделирования стендовых испытаний в аэродинамической трубе в этой СКO .
Основная форма выражения аэродинамических сил , , , :
где i – вид силы (d (драг) или l (лифт); cd и cl – соответствующие аэродинамические коэффициенты).
Для аэро-питч-момента (АПМ):
Коэффициенты cd, cl, cm, получаемые по результатам испытаний объектов в аэродинамической трубе, в данном исследовании полагаем зависимыми от скоростного режима ТС или его масштабной модели.
2.5. Привлечение результатов испытаний эталонных ПОТ к ПИМ квантомобиля
В общепринятой практике аэродинамических исследований первостепенным при разномасштабном моделировании аэродинамических тел является соблюдение равенства чисел Рейнолдса Re, определяемых по базовому параметру – либо по длине тела ReL, либо по высоте тела ReH, либо по квадратному корню фронтальной площади ReS, либо по приведенному диаметру тела ReD. Остановимся на длине тела L. Между числом ReL и скоростью невозмущенного набегающего потока воздуха V∞ имеется прямолинейная зависимость:
где υ – коэффициент кинематической вязкости воздуха , , .
Одними из передовых работ по исследованию характера зависимостей аэродинамических коэффициентов cd, cl, cm от чисел Рейнолдса для автомобилей и их ПОТ типа 1-Box, являются диссертации Newnham P.S. и Perry A.K. . В этих работах упомянутое требование равенства чисел Re корректируется введением критических значений числа Re (соответствующих началу и концу срыва потоков), выше которых требование равенства чисел Re смягчается – лишь бы число Re было выше посткритического значения. Построили график, являющийся упрощенным обобщением этих работ – рис. 2 (на котором оси скоростей V1-Box и VКамАЗ определяются по уравнению (6)). Видим три характерных участка, для каждого из которых свойственно свое состояние воздушного потока, обтекающего тело. При малых числах Re (соответственно малых V∞) ReL <1,8*106 наблюдается предкритическая (Pre–critical) зона с ниспадающим cd (с падением от уровня cdVnul для скорости Vq=0). Примерно при ReL ~ 1,8*106 (Critical Re) начинается процесс срыва потока. Этот процесс Transitional (со значительным падением cd) развивается до Re ~ 2,3*106. При более высоких значениях числа Re господствует посткритическая (Post–critical) зона c устойчивым низким cd.
Видим, например, что пост–критическая зона для ПОТ 1-Box (длиной 0.845 м) охватывает скорости V >40 м/с, а для тела профиля 1-Box с габаритами автомобиля КамАЗ-4326 (длиной 7,3 м) зона охватывает скорости V >4,63 м/с .
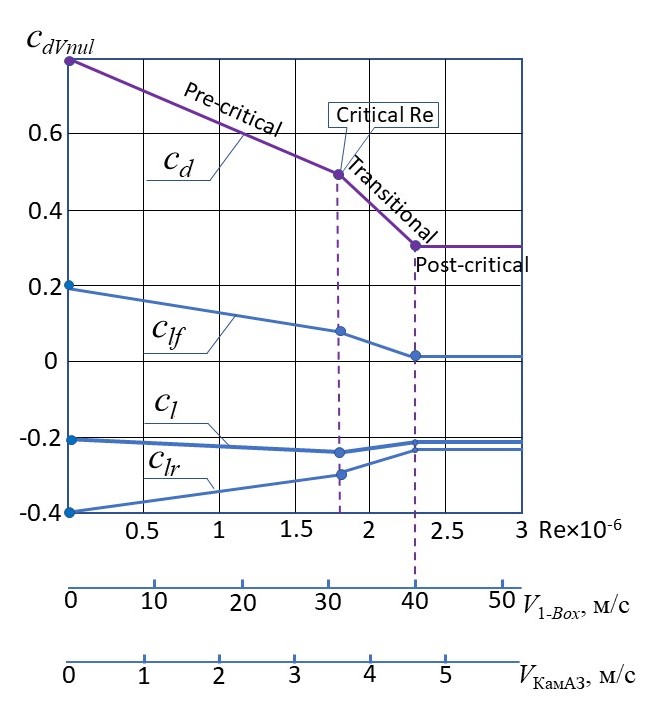
Рисунок 2 - Кусочно-линейное представление динамики изменения аэродинамических коэффициентов при изменении числа Re и скорости тела V: V1-Box и VКамАЗ – скорости обдува ПОТ 1-Box (длиной 0,845 м) и ПОТ с пропорциями 1-Box величиной с КамАЗ-4326 (длиной 7,3 м), соответственно
Рассмотренный аналитический материал использован при формировании имитационной системы МПДК. Две базовые подсистемы МПДК: продольной динамики экипажа (Vehicle Dynamics), а также расчета нормальных реакций и питч-моментов (NormReactions) – представлены в авторских работах , .
2.7. Масштабное совмещение конкретного автомобиля-аналога и вариантов ПОТ
Для отработки и верификации модели, а затем проведения на ее основе ПИМ движения квантомобиля необходимо привлечение конструктивных и эксплуатационных характеристик существующих автомобилей. Ранее автором для обоснования силового баланса и представления динамики продольного движения квантомобиля в качестве аналога использовался автомобиль КамАЗ-4326. Накопленный материал определил КамАЗ-4326 в качестве основного аналога и в данной работе. Рассмотрение аэродинамики движения потребовало привлечения данных и по некоторому множеству ПОТ , , , .
Условимся, для краткости, называть модели полнонатурных размеров ТС – макромоделями, а масштабированные модели малых размеров – микромоделями.
Хотя по каждому упомянутому во введении ПОТ множество публикаций содержит разнообразие реализованных векторов значений Ci ={cd, cl, cm} (это объясняется целями, методиками и условиями проведения исследований), все же в целом микромодели этих ПОТ можно расположить в следующий ряд с совершенствованием профиля и улучшением их аэродинамики: 1-Box , , 2-Box , , Ahmed , Windsor , Docton , Davis , , .
Для методической отработки прогнозирования устойчивости квантомобиля выбрали из этого ряда два крайних варианта ПОТ с двумя противонаправленными (оппозитными) компонентами вектора Ci:{cd = 0,38; cl = –0,22; cm =0,11} для 1-Box и {cd=0,263; cl=0,42; cm= –0,35} для Davis. (см. рис. 3)
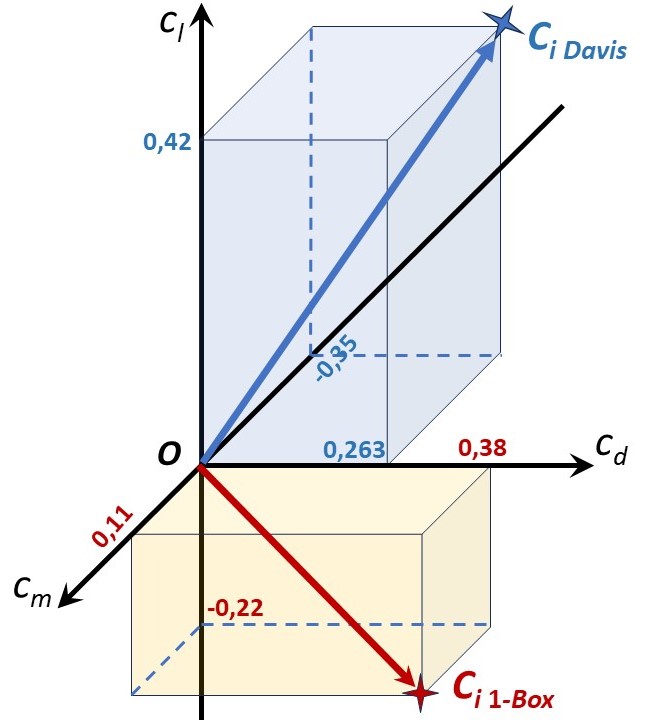
Рисунок 3 - Представление оппозитных вариантов ПОТ: 1-Box и Davis
Рассмотрим привлечение материалов по аэродинамике ПОТ 1-Box к построению аэродинамического паспорта квантомобиля-аналога КамАЗ-4326.
Полнонатурный КамАЗ-4326 имеет габаритные размеры L:W:H (м): 7,3:2,55:3,3 (соотношение 1:0,35:0,45). Представленная в литературе модель 1-Box имеет размеры 0,845:0,39:0,38 м (соотношение 1:0,46:0,45). Как видим, пропорции отличаются (по ширине), что отражено на рис. 4a, где параметром масштабирования выбрана длина объекта.

Рисунок 4 - Совмещение геометрических моделей 1-Box и КамАЗ-4326:
а - масштабирование по длине экипажа; b - масштабирование по ширине экипажа
Всё же, оценив экспертно, для методической проработки оставили вариант a, с учетом в расчетах разницы фронтальных площадей объектов. Для этого варианта коэффициент масштабирования линейных размеров KL= 7,3 / 0,845 = 8,639. Для площадей – KS = KL2= 74,63. Для объемных, массовых и силовых величин – KM = KL3= 644,75.
Для имитации посредством представленной выше S-модели проведена подготовка шести вариантов расчетных объектов, помещенных в табл. 1. Это – полнонатурный КамАЗ-4326 и его микромодель в масштабе 1: 8,639; 1-Box тело исходного размера , а также его макромодель в масштабе KL = 8, 639; Davis тело исходного размера , а также его макромодель в масштабе KL = 5,659. Макромодели 1-Box и Davis сформированы с доведением до длины 7,3 м.
В табл.1 жирным шрифтом занесены первоначальные, исходные величины, а простым шрифтом – полученные расчетом с прямым или обратным использованием коэффициентов подобия KL, KS и KM. Отметим, что использование коэффициента KM для силовых воздействий при масштабном преобразовании объясняется прямой связью между силой и массой, на которую сила действует.
Таблица 1 - Данные по разномасштабным аэродинамическим моделям КамАЗ-4326, 1-Box и Davis
Параметр | Условный номер модели | |||||
1 | 2 | 3 | 4 | 5 | 6 | |
КамАЗ исходная макромодель | Мод. КамАЗ 1/KL= 1/8.639 микромодель | Мод. 1-Box KL= 8.6397 макромодель | 1-Box исходная микромодель | Davis KL= 5.659 макромодель | Davis исходная микромодель | |
L, м | 7,3 | 0,845 | 7,3 | 0,845 | 7,3 | 1,29 |
W, м | 2,55 | 0,295 | 3,37 | 0,39 | 2,55 | 0,45 |
H, м | 3,3 | 0,382 | 3,28 | 0,38 | 1,87 | 0,33 |
Sfr, м2 | 8,415 | 0,1127 | 11,05 | 0,1482 | 4,76 | 0,1485 |
Lwb, м | 4,25 | 0,492 | 4,25 | 0,492 | 4,87 | 0,860 |
L2, м | 2,125 | 0,246 | 2,125 | 0,246 | 2,435 | 0,430 |
Hg, м | 1,3 | 0,1505 | 1,3 | 0,1505 | 0,9 | 0,159 |
HFtx, м | 1,0 | 0,1158 | 1,0 | 0,1158 | 0,8 | 0,141 |
Hw, м | 1,6 | 0,190 | 1,6 | 0,190 | 1,0 | 0,177 |
LFtz, м | 0,5 | 0,05787 | 0,5 | 0,05787 | 0,5 | 0,088 |
rd, м | 0,5 | 0,05787 | 0,5 | 0,05787 | 0,5 | 0,088 |
m, кг | 8970 | 13,912 | 8970 | 13,912 | 8970 | 49,5 |
Gq, Н | 88000 | 136,49 | 88000 | 136,49 | 88000 | 485,65 |
FT, Н | 90000 | 139,59 | 90000 | 139,59 | 90000 | 496,7 |
KL | 8,6397 | 1 | 8,6397 | 1 | 5,659 | 1 |
KS | 74,63 | 1 | 74,63 | 1 | 32,02 | 1 |
KM | 644,75 | 1 | 644,75 | 1 | 181,2 | 1 |
SqrSfr | 2,901 | 0,336 | 3,324 | 0,385 | 2,182 | 0,385 |
KSfr | 0,397 | 0,397 | 0,455 | 0,455 | 0,299 | 0,299 |
V∞, м/с | 5 | 40 | 5 | 40 | 5 | 40 |
cd | 0,38 | 0,38 | 0,38 | 0,38 | 0,263 | 0,263 |
cl | –0,22 | –0,22 | –0,22 | –0,22 | 0,42 | 0,42 |
cm | 0,11 | 0,11 | 0,11 | 0,11 | –0,35 | –0,35 |
В табл. 1 в строку HFtxзанесены гипотетические исходные значения высоты действия вектора траста. В процессе ПИМ они могут меняться по потребности, вплоть до HFtx = 0, когда надо представить классический автомобиль с реализацией тяги в пятнах контакта ведущих колес автомобиля с ОП.
3. Основные результаты
3.1. Подготовка и план расчетов
Опорными значениями параметров приняты помещенные в табл. 1. Обоснование базовых данных по макромодели КамАЗ-4326 (колонка 1) можно найти в авторских работах , , . Массу модели КамАЗ-4326 m = 8970 кг использовали и для других макромоделей. Для всех вариантов моделей приняли базовые значения fkv = 0,00037 с2/м2; ρw = 1,225 Н с2/м4; δwh = 0,04; β = 0º. Максимальное значение траста FT = 90000 Н выбрано из условия, что при угле β = 77.9º оно (в соответствии с (1)) обеспечивает полное вывешивание экипажа весом 88000 Н, оставляя FTx = 18865 Н на обеспечение горизонтального движения (см. подробнее в ).
Размерности величин на всех результирующих графиках следующие: [Ftx, Ftz, Fa, Fr, Fwx, Fwz, Rz1st] = Н; [Mftx, Mftz, Mfa, Mfr, Mfwx, Mfwz, Mst] = Нм; [KMFw.Mst] = 0; [Acceleration] = м/с2; [Velocity] = м/с; [Distance] = м.
3.2. Расчеты на микромоделях
Сначала рассчитали для микромодели автомобиля 1-Box ТСМ Mst (обратный аэро-питч-моменту) путем реконструкции стендовых испытаний в автомобильном варианте (HFTx=0 м), задав fk0=0 и скорость обдува V∞ = 40 м/с. Результаты на рис. 5а. Затем спрогнозировали ТСМ для микромодели квантомобиля 1-Box (HFTx = 0,1158 м) для тех же остальных условий (рис. 5б).
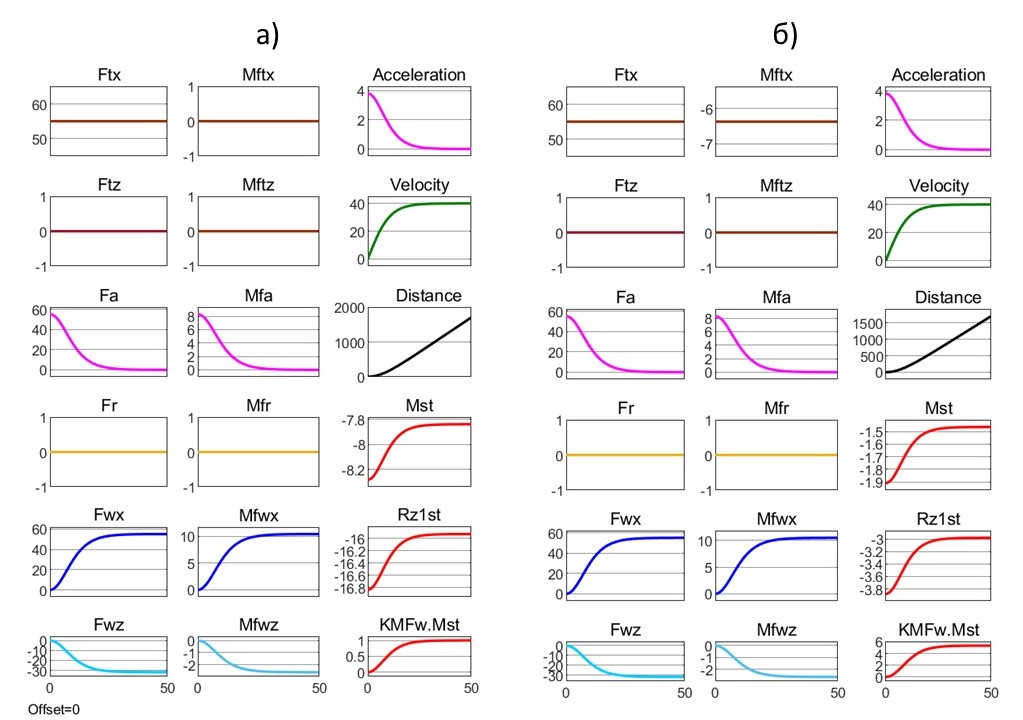
Рисунок 5 - Графики изменения основных показателей при виртуальном разгоне микромодели 1-Box (с данными по табл. 1) до скорости Vust = 40 м/с при fk0 = 0 и соответствующем постоянном значении вектора траста FTx = 55 Нм в двух вариантах:
а - автомобильный (HFTx = 0 м); б - квантомобильный (HFTx = 0,1158 м)
Аналогичные расчеты произвели и для микромодели Davis: а) автомобильный вариант; б) квантомобильный вариант. Здесь для достижения Vust = 40 м/с понадобился FTx = 38,3 Нм (см. рис. 6).
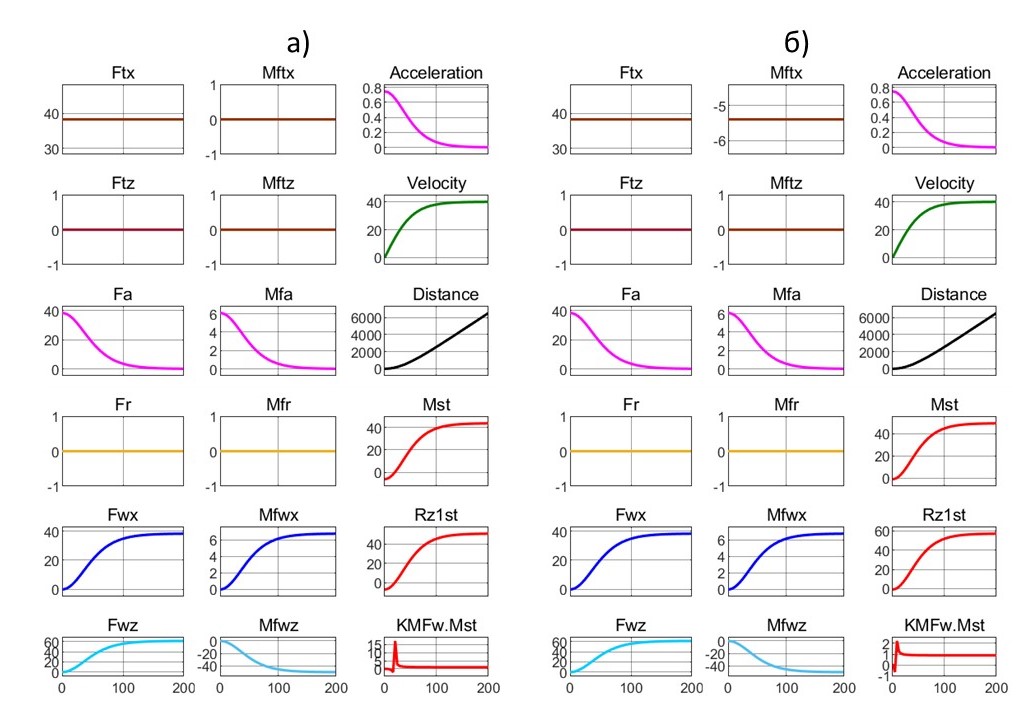
Рисунок 6 - Графики изменения основных показателей при виртуальном разгоне микромодели Davis (с данными по табл. 1) до скорости Vust = 40 м/с при fk0 = 0 и соответствующем постоянном значении вектора траста FTx == 38,3 Нм в двух вариантах:
а - автомобильный (HFTx = 0 м); б - квантомобильный (HFTx = 0,141 м)
Для сравнительного анализа топологии зависимостей ТСМ Mst от коэффициента сопротивления fk0 для скорости установившегося движения Vust =40 м/с провели расчеты для микромодедей 1-Box и Davis – рис.7.
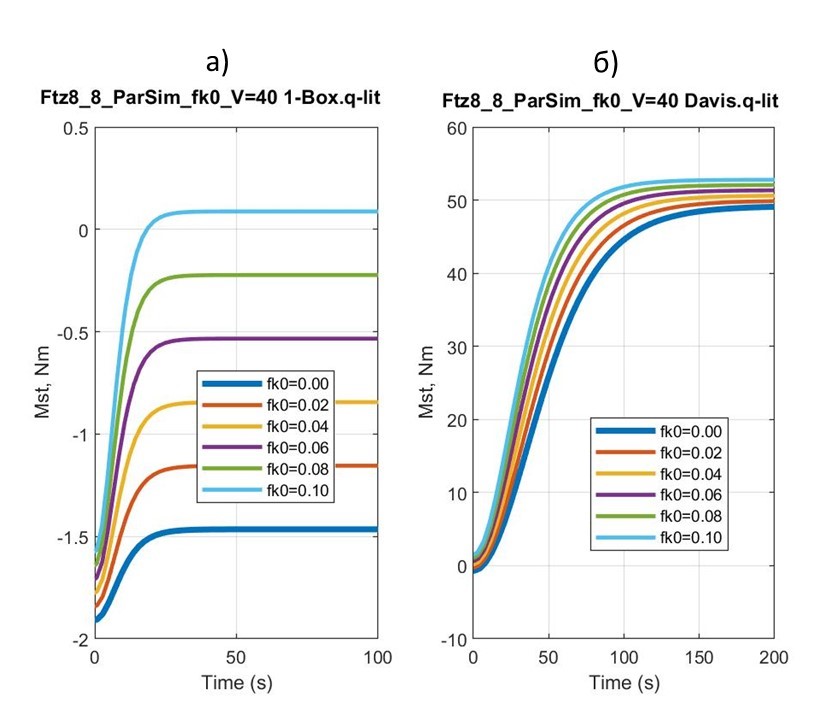
Рисунок 7 - Графики изменения ТСМ Mst при разгоне микромоделей 1-Box (а) и Davis (б) до соответствующего Vust при различных fk0

Рисунок 8 - Графики зависимости ТСМ при разгоне микромодели 1-Box до заданной скорости Vust =40 м/с при различных значениях fk0 и сменой высоты действия траста от HFTx =0 м (автомобильный вариант – рис. 8а) до HFTx =0,1158 м (квантомобильный вариант № 4 по табл. 1– рис. 8г)
Сравнительный расчет зависимости ТСМ от значений fk0 при разгоне макромоделей 1-Box и Davis при постоянной величине траста FTx =10 кН – на рис. 9.
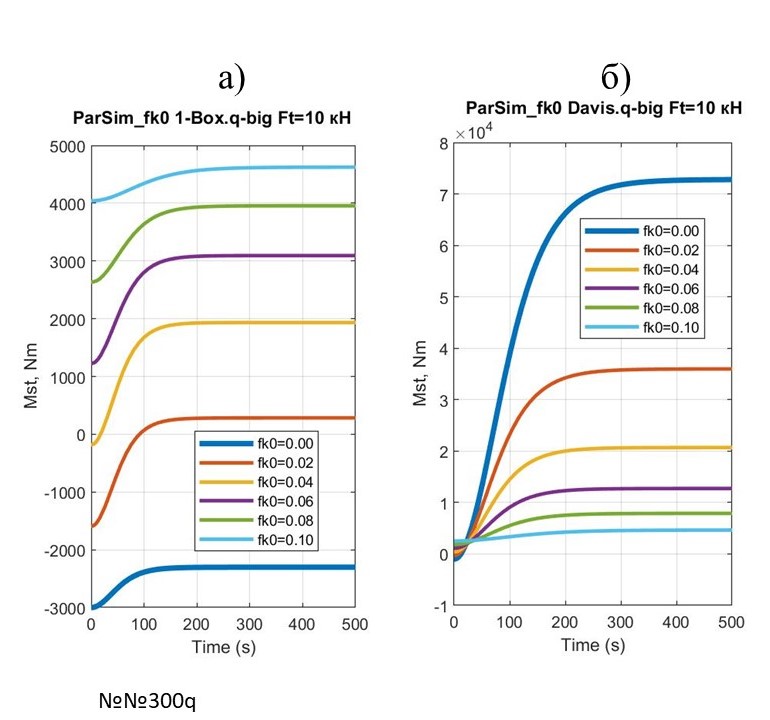
Рисунок 9 - Графики зависимости ТСМ от значений fk0 при разгоне макромоделей 1-Box и Davis при постоянной величине траста FTx =10 кН
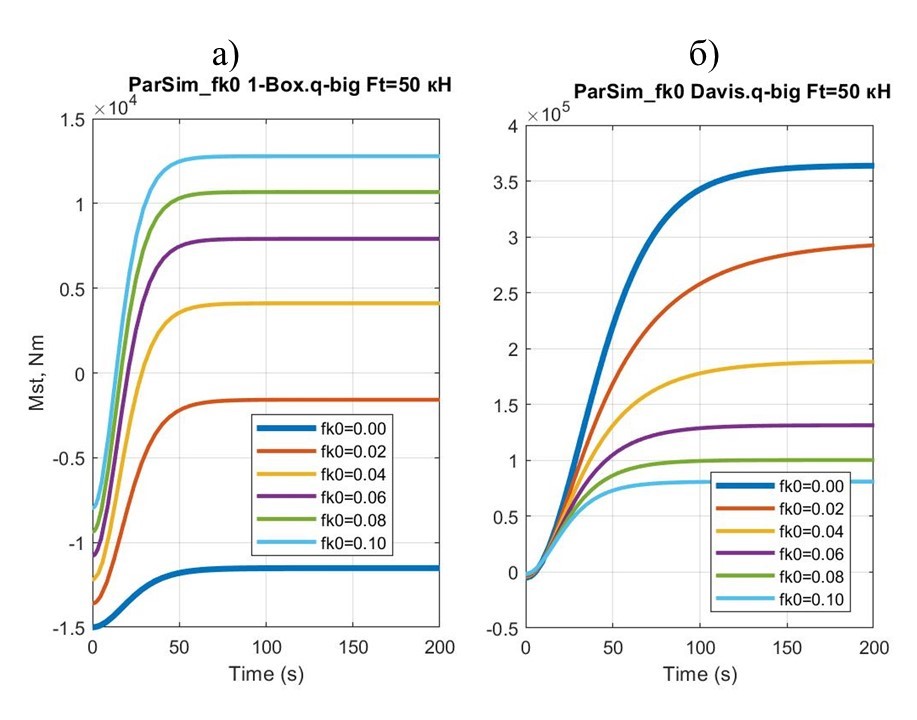
Рисунок 10 - Графики зависимости ТСМ от значений fk0 при разгоне макромоделей 1-Box и Davis при постоянной величине траста FTx =50 кН
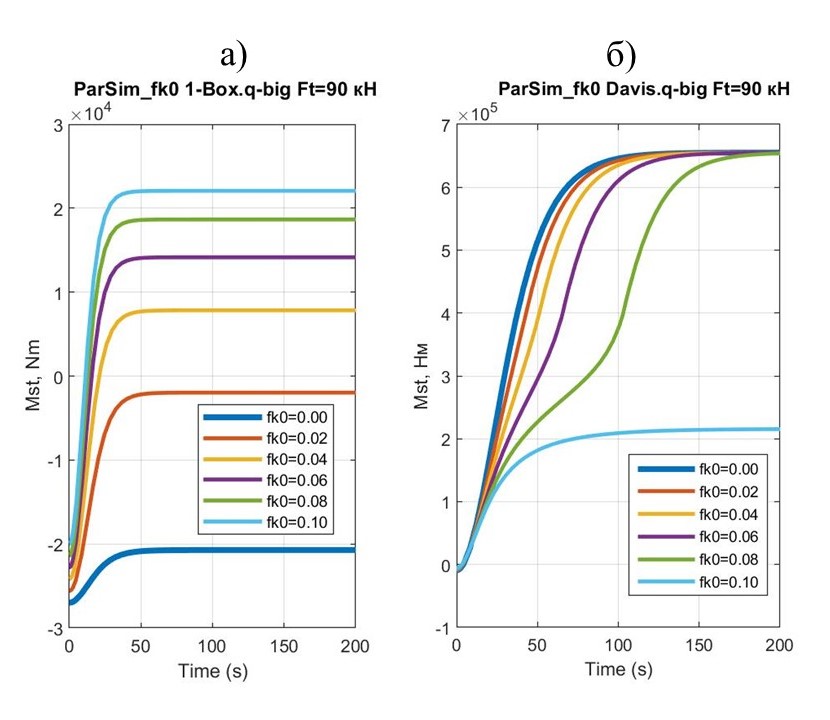
Рисунок 11 - Графики зависимости ТСМ от значений fk0 при разгоне макромоделей 1-Box и Davis при постоянной величине траста FTx =90 кН
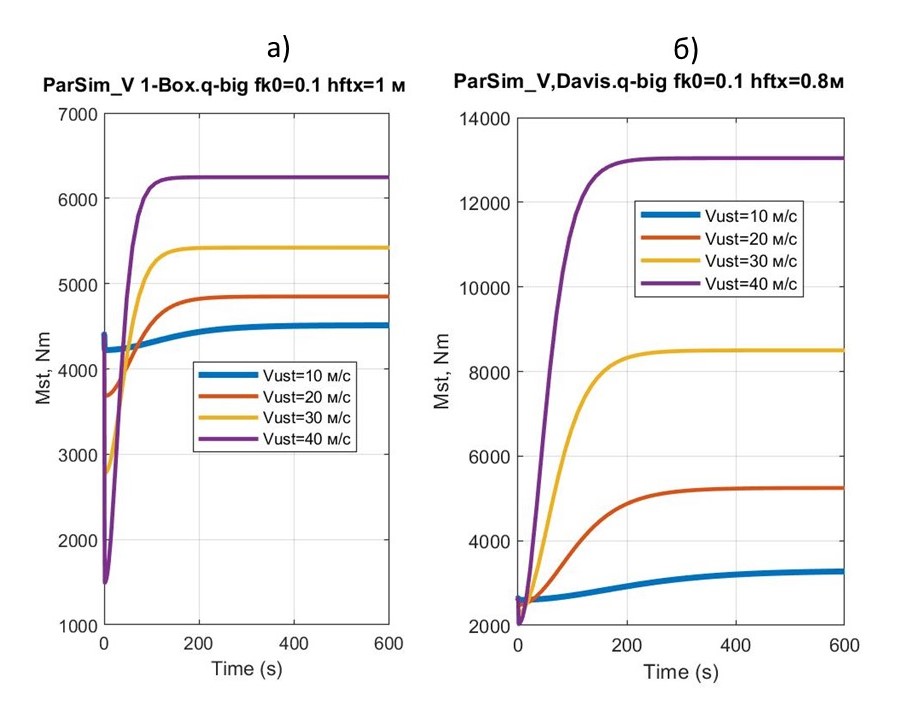
Рисунок 12 - Графики изменения Mst в процессе разгона макромоделей квантомобилей 1-Box и Davis с выходом на заданные скорости установившегося движения Vust при fk0 = 0.1
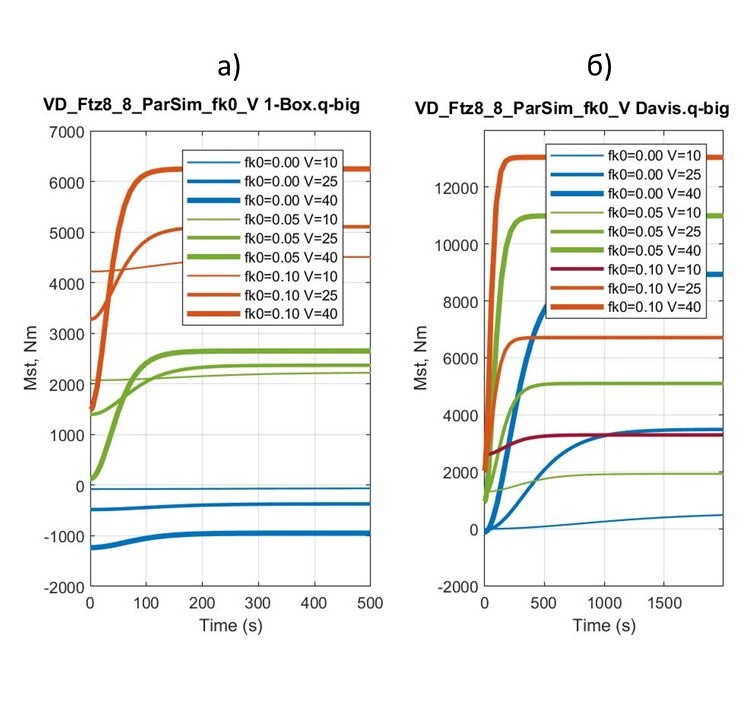
Рисунок 13 - Графики изменения Mst в процессе разгона макромоделей 1-Box и Davis для ряда fk0 (0; 0,05; 0,10) с выходом на заданные скорости Vust (10; 25; 40 м/с).
4. Обсуждение
В предыдущих работах автора , , , , закладывались основы Simulink-моделирования движения квантомобиля, настраивались объекты-прототипы из числа существующих наземных ТС, в том числе и задействованный здесь КамАЗ-4326. Это позволило развить S-модель до уровня МПДК (частично представленного в работе ) и провести с ее помощью расчетное исследование продольной устойчивости квантомобиля при аэродинамических конфигурациях кузова, представляемых эталонными ПОТ.
Из методических построений отметим кусочно-линейный примитив представления динамики изменения аэродинамических коэффициентов при изменении числа Re и скорости тела V (рис. 2). Естественно, аэродинамические процессы в докритической зоне характеризуются большим (и трудно оцениваемым) разбросом значений cd, cl, cm. Но при малых скоростях движения ТС доля АПМ в суммарном питч-моменте мала, так что её погрешностью можно пренебречь – ради непрерывности расчета в зоне малых скоростей.
В посткритической зоне постоянство значений названых коэффициентов за скоростными пределами, обусловленными проведенными натурными аэродинамическими испытаниями, – тоже проблематично. Сознавая это, а также учитывая большой вклад АПМ в баланс моментов на высоких скоростях (соответственно, и большой вклад АПМ в погрешность расчета показателей движения), автор всё же (без привлечения критериев Маха и Строхаля) осуществлял расчеты для этих скоростей в целях методической отработки развиваемых концепций и ПИМ.
Основные расчеты, однако, проведены с микромоделями для скоростей 40 м/с, а для макромоделей – более 10 м/с (см. рис. 2).
Относительно данных табл. 1. Перенос значения вектора Ci {cd = 0.38; cl=–0.22; cm=0,11} из данных по модели 1-Box на модели КамАЗ-4326 нужно признать весьма условным при масштабной трансформации по варианту рис. 4а.
Обсуждение результатов расчетов начнем с рассмотрения графиков на рис. 5, отображающих реконструкцию в МПДК стендового экcперимента Ньюнхема с микромоделью 1-Box. Напомним, что МПДК рассчитывает разгон масштабной модели с определенными геометрическими, массовыми и весовыми характеристиками (см.табл. 1) с выходом на скорость установившегося движения Vust – так бы складывались графики изменения представленных параметров движения модели по ОП. Но поскольку масштабная модель прикреплена к стенду, изменение скорости (Velocity), ускорение (Acceleration) и дистанцию (Distance) следует «читать» как изменение скорости и ускорение набегающего потока воздуха V∞, а также путь, реализуемый воздушным потоком относительно покоящейся модели. Сила инерции массы модели (Fa) носит в данном случае условный характер (хотя при необходимости ее носителем можно определить эквивалентную массу воздуха и искать во внешнем контуре стенда). ТСМ Mst в условиях крепления модели к столу стенда – есть силовой питч-момент, выдерживаемый конструкцией стенда. Сила Rz1st при этом – нормальная реакция передней опоры модели.
Сравнивая на риc. 5 автомобильный (а) и квантомобильный (б) варианты модели 1-Box, видим, что появившийся у квантомобиля момент Mftx = –6,374 Нм как раз равен разнице Mst левого (а) и правого (б) вариантов ТС (–7.839 – –1.465 = –6,374).
Аналогичные построения и расчеты для микромодели КамАЗ позволили получить мало отличающиеся (качественно) результаты: Mftx = –5,978 – –1,118 = –4,86 Нм (на отдельный рис. не вынесено).
Сравнивая на риc. 6 автомобильный (а) и квантомобильный (б) варианты модели Davis, видим, что появившийся у квантомобиля момент Mftx = –5,4 Нм как раз равен разнице Mst левого (а) и правого (б) вариантов ТС (43,6 – 49,0= –5,5). Но разительным явилось отличие величины Mst микромодели квантомобиля Davis от таковой для 1-Box и КамАЗ (49 Нм против –1÷–1,5 Нм) – то есть для Davis характерна необходимость в большом стабилизирующем моменте, нейтрализующем клюющий питч-момент.
В силу незначительной разницы показателей 1-Box и КамАЗ (на фоне Davis) и было признано целесообразным в дальнейшем противопоставлять модели Davis только одну из оставшихся моделей: 1-Box.
Анализируя графики на рис. 7, можно отметить, что микромодель квантомобиля 1-Box при значениях fk0 = 0 ÷ 0,08 требует нейтрализации положительного (задирающего) питч-момента. Микромодель же Davis при всех значениях fk0 = 0 ÷ 0,10 требует нейтрализации отрицательного (клюющего) питч-момента.
Серией расчетов обнаружено, что смена высоты действия траста может приводить не только к смещению семейства кривых зависимости Mst от дорожного сопротивления fk0, но и способна изменить топологию соответствующей поверхности отклика. Это можно видеть на примере рис. 8. Видим, что при Hftx=0.0579 м (экспозиция б) ТСМ Mst ≈ – 4,65 Нм для всех fk0 = 0 ÷ 0,1. А далее (при Hftx >0,0579 м – экспозиции в и г) семейство кривых даже «опрокидывается».
Расчеты на макромоделях в целом позволили отметить подобие топологии семейств кривых (поверхностей) для микро- и макромоделей. В подтверждение можно сравнить графики для моделей 1-Box на рис. 8г и рис. 9а (за исключением зоны малых скоростей).
Итоги обсуждения ПИМ макромоделей 1-Box и Davis (по рис. 9 ÷ 13) приведем в виде табл. 2.
Таблица 2 - Сравнение диапазонов и разбросов ТСМ макромоделей 1-Box и Davis в различных ситуациях
№ рисунка | 1-Box | Davis | ||
Диапазон ТСМ, Нм | Разброс ТСМ, Нм | Диапазон ТСМ, Нм | Разброс ТСМ, Нм | |
9 | –2200 ÷ 4600 | 6800 | 72000 ÷ 2000 | –7000 |
10 | –12000 ÷ 13000 | 25000 | 360000 ÷ 80000 | –280000 |
11 | –21000 ÷ 22000 | 3000 | 660000 ÷ 220000 | –440000 |
12 | 4500 ÷ 6200 | 1700 | 3300 ÷ 13000 | 9700 |
13 | 0 ÷ 6000 | 6000 | 200 ÷ 1300 | 12800 |
Обобщая анализ графиков, отметим следующее. Диапазоны и разброс значений ТСМ у макромодели Davis гораздо шире, чем у 1-Box. При этом, если ТСМ у 1-Box в зависимости от сочетания дорожного сопротивления и скоростей движения может быть как отрицательным, так и положительным, то у Davis ТСМ всегда положительны (т.е. направлены на нейтрализацию клюющего питч-момента).
Выбранные для расчетов модели ПОТ с крайними, оппозитными значениями вектора Ci позволили выявить существенную разницу питч-моментов, возникающих при различных сочетаниях скоростей движения ТС и дорожного сопротивления и отличающихся как по величине, так и по направлению. Промежуточные значения вектора Ci, очевидно (в силу компактности и непрерывности пространства размещения этого вектора), будут приводить к промежуточным ситуациям и результатам ПИМ .
5. Заключение
Авторская Simulink-модель приземного движения квантомобиля (МПДК), настроенная на решение задач исследования с привлечением материалов испытаний эталонных аэродинамических моделей автомобилей, позволила провести расчетное исследование динамики и устойчивости продольного движения квантомобиля.
В целом, подтвердилась гипотеза: уровень и характер питч-момента квантомобиля отличается от такового для автомобиля. Он может быть значительным, иногда меняя направленность (относительно автомобильного варианта ТС) и требует его оперативной нейтрализации (минимизации).
Основными средствами минимизации питч-момента могут быть следующие: жесткие конструктивные (обводы и оперение корпуса); выдвижное оперение; дополнительные стабилизирующие трастеры; специальные приемы вождения.
На основе результатов ПИМ показана значимость проблемы обеспечения продольной устойчивости квантомобиля. Основными факторами, усугубляющими названую проблему, в сравнении с классическим автомобилем, являются возникновение и реализация тяговой силы над опорной поверхностью, что увеличивает опасность опрокидывания.
Сформированные на базе программы МПДК методические положения оценки продольной устойчивости квантомобиля могут послужить основой расчетной оптимизации компоновок этого вида ТС, расположения силовых модулей (трастеров) и их задействования в процессе движения.
МПДК можно рассматривать как важную компоненту структуры дальнейших исследований квантомобиля.
