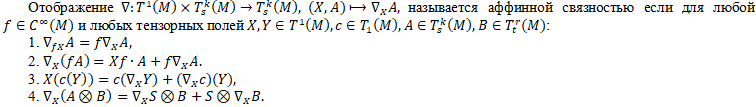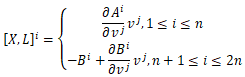ALTERNATIVES TO THE EGOROV'S AND KOBAYASHI'S THEOREMS ON COMPLETE AFFINE CONNECTIONS

АНАЛОГИ ТЕОРЕМ ЕГОРОВА И КОБАЯСИ О ПОЛНЫХ АФФИННЫХ СВЯЗНОСТЯХ

Научная статья

Кальницкий В.С.*

ORCID: 0000-0002-3937-6078,

Санкт-Петербургский государственный университет, Санкт-Петербург, Россия

* Корреспондирующий автор (st006987[at]spbu.ru)

Аннотация

В статье подводится итог исследований автора по вопросу полноты геодезических потоков аффинных связностей и их симметрий. Целью исследования является поиск и описание линейных пространств полных полей на касательном расслоении. В статье доказаны три новых результата. Полученные теоремы являются аналогами теоремы Кобаяси о полной аффинной связности. Рассмотрены метрическая (теорема 7) и аффинная (теорема 8) ситуации. Доказан аналог теорем Егорова о лакунарности в размерностях полных многообразий. Доказана оценка границы размерности пространств полных полей единичного ранга, влекущей полноту самой связности (теорема 10). Предложена схема получения аналогичных оценок границы размерности пространства полных полей старших рангов. Намечены пути дальнейшего исследования. Полученные результаты могут быть использованы при классификации аффинных связностей, допускающих обширные алгебры симметрий геодезического потока.

Ключевые слова: аффинная связность, геодезический поток, симметрия связности, полное векторное поле.

ALTERNATIVES TO THE EGOROV'S AND KOBAYASHI'S THEOREMS ON COMPLETE AFFINE CONNECTIONS

Research article

Kalnitsky V.S.*

ORCID: 0000-0002-3937-6078,

Saint Petersburg State University, Saint Petersburg, Russia

* Corresponding author (st006987[at]spbu.ru)

Abstract

The article concludes the research of completeness of the symmetry and geodesic flow of affine connections. The study aims to find and describe linear spaces over complete fields on the tangent bundle. The article verifies 3 new results. The developed theorems are alternatives to the Kobayashi's theorem on complete affine connections. The study examines a metric situation (theorem 7) and an affine situation (theorem 8). The article verifies an alternative to the Egorov's lacunarity in complete manifold dimensions. The paper verifies the evaluation of dimension borders of the first-order complete field which allows completeness of the connection itself (theorem 10). The article suggests a scheme of obtaining an alternative evaluation of higher order complete field dimension borders. The study sets up the ways of further research. The results could be used to classify the affine connections that accept extensive symmetry algebras of the geodesic flow.

Keywords: affine connection, geodesic flow, symmetric connection, complete vector field.

Основные определения и обозначения

В этой работе многообразия и тензорные поля на них мы будем считать бесконечно дифференцируемыми. Мы будем придерживаться терминологии принятой в [1], упомянутые в этом разделе факты можно найти там же. Пространство тензорных полей типа (k,s) (k раз контравариантных, s раз ковариантных) на многообразии M мы будем обозначать  символом  – алгебру -гладких функций на M.

Рассмотрим многообразие М и векторное поле  Для каждой точки  существует окрестность  такие, что для каждой точки  интегральная кривая  определена на интервале. Таким образом, для любого  определено отображение  Совокупность всех таких локальных диффеоморфизмов, определяемых полем X, называется локальным потоком  векторного поля X.

Векторное поле X называется полным, если каждая интегральная кривая этого поля определена на всей вещественной оси. Полное векторное поле X определяет однопараметрическую группу диффеоморфизмов многообразия  называемую потоком поля.

Каждое векторное поле X задает отображение  по формуле  Отображение X является дифференцированием алгебры  т.е. оно линейно и для любых функций  выполнено правило Лейбница  Верно и обратное, каждое дифференцирование алгебры  имеет вид  причем поле единственно.

Скобкой Ли двух векторных полей X, Y  называется поле  Относительно введенной операции пространство  всех векторных полей на M является алгеброй Ли.

Каждый диффеоморфизм многообразия  задает отображение  по формуле, записанной в карте    Операция  называется переносом.

Для векторного поля  и тензорного поля  определяется производная Ли поля A по полю X

Для векторных полей верно соотношение 

Перенос векторного поля имеет вид  – дифференциал отображения φ.  Поля  называются j-связанными ([3], т. I). Если поля X и Y являются φ-связанными, то они полны либо неполны одновременно.

Кручением аффинной связности называется тензор  задаваемый соотношением:  Аффинная связность с нулевым кручением называется симметричной. Тензор К определяемый соотношением  называется тензором кривизны связности.

Для векторного поля  отображение  называется ковариантной производной по полю Х. Для координатного векторного поля  отображение   называется частной ковариантной производной  Объект  имеющий в карте  координаты  называется формой связности, его координаты – символами Кристоффеля.

Симметричная аффинная связность на римановом многообразии  называется связностью Леви-Чивиты если для всех наборов индексов выполнено

На касательном расслоении TM риманова многообразия  определена метрика Сасаки  удовлетворяющая следующим свойствам:

1. Отображение  является римановой субмерсией.
2. Сужение на каждый  касательный слой  равно g

Геометрическая однородность

Рассмотрим многообразие M и его касательное расслоение TM. Стандартной картой на TM будем называть карту вида  – карта многообразия M, n - размерность многообразия. Координаты точки  в стандартной карте имеют вид . Векторное поле на TM имеющее в стандартных картах вид  (здесь и далее мы будем придерживаться соглашения Эйнштейна о суммировании по повторяющимся индексам), называется каноническим векторным полем.

Определение 1 ([7]). Векторное поле X на TM называется m-однородным, . Пространство m-однородных полей будем обозначать .

Рассмотрим на TM произвольное поле  Вычислим коммутатор поля X с каноническим полем

Условие однородности при  приводит к тождествам

которые означают однородность координатных функций по второй переменной. Итак, все m-однородные поля в стандартных  координатах  на TM имеют вид

    (1)

где . Так как тензоры  суммируются с вектором v по всем нижним индексам (в инвариантной записи  то поле Y определяется однозначно симметризацией этих полей по ковариантным индексам

где суммирование производится по всем перестановкам σ ковариантных индексов. Мы будем рассматривать лишь симметричные по нижним (ковариантным) индексам тензорные поля .

Введем обозначение для симметризованного по ковариантным индексам тензорного произведения двух полей :  и для симметризованной свертки по индексам 

Определение 2. Рассмотрим тензор . Тензорное поле  называется симметризованной ковариантной производной.

Вторая группа слагаемых в формуле (1), соответствующая тензорному полю Q определяет векторное поле  на TM и называется вертикальным лифтом Q^V тензора Q. Далее однородные поля мы будем записывать как пару .

При наличии аффинной связности существуют различные способы задать векторное поле TM на по тензору A.

Определение 3 ([8]). Полным лифтом  тензорного поля А называется векторное поле на ТМ вида  называется горизонтальным лифтом. Ковариантную валентность тензорного поля А будем называть рангом лифта.

Исходя из формулы (1), если на многообразии определена симметричная аффинная связность ∇, то пространство раскладывается в прямую сумму пространств  полных и вертикальных лифтов тензорных полей. При этом 

В этих обозначениях каноническое поле L может быть записано как  – тождественный оператор.

Определение 4. Полный лифт  поля E называется геодезическим полем  аффинной связности ∇. Связность ∇ называется полной, если полным является поле .

Определение 5. Поле   называется (инфинитезимальная) симметрией геодезического поля, если  

Определение 6. Поле   называется (инфинитезимальной) симметрией аффинной связности, если 

Обзор результатов

Совокупность всех полных векторных полей на многообразии, вообще говоря, не образует линейного пространства. В работе Пале ([2], стр. 99) построен пример двух полных полей, сумма которых не является полным полем. В силу этого обстоятельства стал актуальным вопрос об описании линейных пространств, состоящих из полных векторных полей.

Замечание. Все векторные поля на компактном (замкнутом) многообразии являются полными.

Теорема 1 (Пале [2], стр. 104). Если линейная оболочка некоторого набора полных полей на многообразии и их всевозможных скобок Ли конечномерна, то все поля в ней полны.

Автором в [9] было показано, что полный лифт  тензорного поля  удовлетворяющего уравнению

     (2)

где R – тензор кривизны связности, является симметрией геодезического поля  такие поля будем называть поля Якоби ранга k. Более того, любая однородная симметрия поля  является полем Якоби.

Скобка Ли двух симметрий  является симметрией. Следовательно, на пространстве  тензорных полей, удовлетворяющих уравнению (2), возникает структура бесконечномерной алгебры Ли, названной автором алгеброй Якоби связности [10].

В случае нулевого ранга полный лифт поля X имеет вид  и уравнение (2) является уравнением Якоби. Поле X удовлетворяющее уравнению Якоби, является (инфинитезимальной) симметрией связности ∇ ([6]).

Теорема 2 (Кобаяси Ш., [6], стр. 46). Если аффинная (риманова) связность полна, то любая ее инфинитезимальная симметрия (изометрия) является полной.

В введённых нотациях теорема Кобаяси относится к рангу 0. Целью нашего исследования является доказательство теорем о полноте для симметрий более высокого ранга. Для ранга 1 автором была доказана следующая теорема.

Теорема 3 ([10], стр. 243). Если связность ∇ полна, то полные лифты всех ковариантно постоянных полей  образуют алгебру Ли полных полей.

Из теоремы 3 непосредственно следует, что все симметрии геодезического поля, содержащиеся в описанной алгебре Ли, образуют её подалгебру Ли и полны.

В работе автора [11] удалось продвинуться в вопросе полноты для старших рангов.

Теорема 4 ([11], стр. 52). Рассмотрим тензорные поля  Если связность полна, то полным является поле  являющееся симметрией геодезического поля.

Основной результат. Метрический случай

Определение 7 ([12]). Симметричное тензорное поле  ранга удовлетворяющее соотношению  называется p-киллинговой формой.

Теорема 7. Рассмотрим замкнутое риманово многообразие  и тензорное поле  Если  то поле   является полным.

Отметим, что на замкнутом многообразии геодезическое поле связности Леви-Чивита является полным, так как его поток сохраняет длины векторов, т.е. сохраняет расслоение метрических шаров, являющееся компактом. Доказательство теоремы 7 основано на следующей лемме.

Лемма 1. На римановом многообразии  поток полного лифта  тензорного поля  – p-киллингова форма, сохраняет расслоение метрических шаров риманового многообразия М.

Доказательство. Достаточно показать, что в каждой точке  вектор поля  ортогонален вектору  в смысле метрики Сасаки на TM ([13]), сужение которой на каждый слой  совпадает с g. Выберем в точке   нормальную (экспоненциальную) карту многообразия M. В этой карте в точке x форма связности тривиальна  и, следовательно, скалярное произведение на касательном слое относительно метрики Сасаки имеет единичную матрицу Грама, т.к. метрика Сасаки на слоях TM совпадает с метрикой. Вектор поля  в точке  имеет вид

Скалярное произведение с вектором  вычисляемое как обычное скалярное произведение в ортонормированном базисе  (символ Кронекера), равно

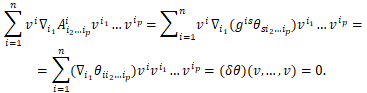
Таким образом, поле  ортогонально в каждой точке каноническому векторному полю L на TM. С другой стороны, каноническое поле L ортогонально (2n-1)-мерному расслоению метрических шаров фиксированного радиуса в метрике Сасаки, рассматриваемому как подмногообразие TM. Действительно, поле L ортогонально (n-1)-мерной касательной плоскости метрического шара в касательном слое и n-мерному горизонтальному слою многообразия в данной точке. Последнее следует из того, что по определению метрики Сасаки проекция является римановой субмерсией. Следовательно, поле  касается расслоения метрических шаров над  M.

Доказательство теоремы. С помощью метрики опустим верхний индекс поля  и убедимся, что получившееся тензорное поле θ является  - киллинговой формой. Действительно, симметризация тождества

запишется как  по условию. Первое слагаемое в полученной сумме равно нулю по определению связности Леви-Чивита.

Далее, согласно лемме поток поля  сохраняет расслоение шаров. Так как по условию теоремы риманово многообразие компактно, то расслоение шаров является замкнутым многообразием, и любое поле касательное к нему, в частности  является полным.

Следствие. На замкнутом римановом многообразии полный лифт  любого ковариантно постоянного тензорного поля  является полным векторным полем на TM. 

Основной результат. Аффинный случай

В работе автора [13] было доказано, что поднятие индекса p-киллингова поля определяет поле Якоби для любого [15]), т.е. пространство p-киллинговых форм вкладывается в пространство полей Якоби ранга  В следующей теореме будет показано, как возможно при отсутствии метрики вложить ковариантно постоянные формы ранга p в поля Якоби ранга 

Теорема 8. На многообразии с полной аффинной связностью каждая симметрия геодезического потока ранга  имеющая вид   является полной.

Разобьём доказательство на несколько шагов.

Лемма 2. Рассмотрим аффинное многообразие  является p-киллинговой формой  – поле Якоби ранга  тогда тензор  является полем Якоби ранга

Доказательство. Полным лифтом p-формы на касательное расслоение называется функция  Как было доказано в [14], форма θ является киллинговой, если ее полный лифт эквивариантен относительно геодезического потока на касательном расслоении . По определению, поле A является полем Якоби если его полный лифт эквивариантен относительно геодезического потока  Рассмотрим произведение полных лифтов  и убедимся, что оно эквивариантно

Вычислим полный лифт поля 

Что и требовалось доказать.

Лемма 3. Рассмотрим аффинное многообразие  – невырожденный как линейный оператор на касательном слое в некоторой точке М тогда поля  являются полными или неполными одновременно.

Доказательство. Если ковариантно постоянный тензор как линейный оператор на касательном слое невырожден в какой-либо точке многообразия, то он невырожден всюду.  Полный лифт киллинговой формы  является интегралом геодезического потока, так как .  Следовательно, поле  полное, т.к. вдоль каждой траектории векторное поле умножается на константу. Перенос полного поля с помощью произвольного диффеоморфизма многообразия даст полное поле. Перенесем поле  с помощью диффеоморфизма, задаваемого послойным изоморфизмом

Равенство  доказано в [10] (теорема 5.1), в частности, для ковариантно постоянного поля A Осталось показать, что правая часть равенства является полным лифтом поля  Действительно,

Последнее верно, в силу ковариантной постоянности поля A и равенства

Лемма 4. Рассмотрим аффинное многообразие   – невырожденный оператор на касательных слоях, тогда поля    являются полными или неполными одновременно.

Доказательство. Рассмотрим форму . Это киллингова форма в силу того, что  является полным одновременно с геодезическим полем.

Лемма 5. Рассмотрим аффинное многообразие  Если геодезический поток полон, то поле  является полным.

Доказательство. Согласно теореме 5.2. [10], в пространстве ковариантно постоянных полей ранга 1 можно выбрать базис из невырожденных полей . По лемме 4 поля  являются полными. Мы докажем, что лифты этих полей коммутируют, тогда, в силу теоремы 1, линейное пространство, ими порожденное, состоит из полных полей. Напомним ([10]), что если    то скобка Ли лифтов лежит в  и имеет вид

где  Рассматриваемые нами поля ковариантно постоянны как тензорные произведения ковариантно постоянных полей, и, значит, коммутируют.

Доказательство теоремы является прямым следствием предыдущих лемм.

Основной результат. Аналог теорем Егорова

В работах И.П. Егорова ([16], [17]) были классифицированы аффинные пространства с обширными группами симметрий и инфинитезимальных симметрий связности (ранга 0 в нашей терминологии). В частности, n-мерное аффинное пространство, для которого размерность r пространства симметрий связности равно  – это евклидово пространство с полной канонической связностью. Пространств   не бывает. Пространства  описаны Егоровым явно – это пространства с полной связностью. И, наконец, не бывает пространств с .

Как следствие прямого описания, результаты Егорова могут быть сформулированы в виде общей теоремы о полноте.

Теорема 9 (Егоров И.П.). Если n-мерное пространство аффинной связности допускает пространство полных симметрий ранга 0 размерности  то связность полна.

Мы докажем аналогичный результат для ранга 1.

Теорема 10. Если аффинная связность на n-мерном многообразии  допускает пространство V полных ковариантно постоянных полей ранга 1 размерности  то связность полна.

Доказательство. Рассмотрим произвольную точку многообразия. Так как ковариантные поля ранга 1 полностью определяются своими значениями в произвольной точке многообразия, то в каждой точке среди полей, составляющих пространство V можно выбрать линейно независимый набор. Если  то в этом наборе существует поле, для которого матрица порождаемого им линейного оператора на слое невырождена в данной точке, а следовательно, не вырождена всюду. В силу леммы 3  связность полна.

Заключение

В случае старших рангов грубую оценку границы размерности пространства полных полей, достаточной для полноты связности, можно получить из следующим образом. Обозначим через s,t размерности пространств ковариантно постоянных аффиноров и полей Киллинга ранга p-1. Выбрав базис из невырожденных аффиноров и тензорно перемножив их с киллинговыми полями, мы получим набор из  s t-мерных линейных подпространств в пространстве ковариантно постоянных тензорных полей, что дает верхнюю оценку на размерность подпространства, не пересекающегося с этой конфигурацией. Если пересечение имеет место, то в силу леммы 4, связность полна. Ясно, что чем шире пространство киллинговых полей, тем эффективнее оценка.

Аналоги теоремы Егорова для больших рангов также могут быть получены с помощью явного описания пространств с обширными пространствами симметрий. Автором в [18] был предложен метод классификации алгебр симметрий на плоских и однородных аффинных пространствах. Полученные результаты выходят за рамки данной статьи.

Конфликт интересов Не указан.

Conflict of Interest None declared.

Список литературы / References

1. Постников М.М. Лекции по геометрии. Гладкие многообразия / М.М. Постников. – М.: Наука. Гл. ред. физ.-мат. лит. – 1987. – 480 с.
2. Palais R. A global formulation of the Lie theory of transformation groups / R. Palais // Mem. Amer. Math. Soc. – 1957. – V. 22. – 123 p.
3. Кобаяси Ш. Основы дифференциальной геометрии / Ш. Кобаяси, К. Номидзу, Т. I. – М.: Наука. – 1981. – 347 c.
4. Шевалле К. Теория групп Ли / К. Шевалле, Т. I. – М.: ИЛ, 1948.
5. Постников М.М. Лекции по геометрии. Группы и алгебры Ли / М.М. Постников. – М.: Наука. Гл. ред. физ.-мат. лит. – 1982. – 447 с.
6. Kobayashi S., Transformation Groups in Differential Geometry / S. Kobayashi. – Springer-Verlag, New York. – 1972. – 190 P.
7. Kawski M. Geometric homogeneity and applications to stabilization / M. Kawski // Proc. IFAC Symp. NCSD. – 1995. – P. 147-152.
8. Crampin M. Applicable differential geometry / M. Crampin, F. A. E. Pirani // London Mathematical Society Lecture Notes Series 59. – Cambridge University Press. – 1986. –394 P.
9. Кальницкий В.С. Автоморфизмы геодезического векторного поля / В.С. Кальницкий // Вестник СПбГУ, сер.1. – 1995. – Вып. 2, №8. – С. 23-24.
10. Кальницкий В.С. Алгебра обобщенных полей Якоби / В.С. Кальницкий // Зап. науч. сем. ПОМИ, "Исследования по топологии", 8. – 1995. – т. 231. – C. 222-243.
11. Кальницкий В.С. Полнота нильпотентных полей / В.С. Кальницкий // Дифференциальная геометрия многообразий фигур. – 2005. – т. 36.– С. 50-53.
12. Степанов С.Е. Об одном применении теоремы Стокса в глобальной римановой геометрии / С.Е. Степанов // Фунд. и прикл. мат. Т.8. – 2002. – №1. – C. 245-262.
13. Sasaki S. On the differential geometry of tangent bundle of Riemannian manifolds / S. Sasaki // Tôhoku Math. J. — 1958. — Vol. 10. — P. 338–354.
14. Kalnitsky V.S. Spray algebra / V.S. Kalnitsky // Proc. Math. Inst. NAS Ukr. – 2004. – V. 50, Part III. – P. 1356-1360.
15. Ashtekar A. A technique for analyzing the structure of isometries / A. Ashtekar, F. Magnon-Ashtekar // J. Math. Phys. – 1977. –V. 19. – P. 1567-1572.
16. Егоров И.П. О порядке групп движений пространств аффинной связности / И.П. Егоров // ДАН СССР. – 1947. – том 57. – № 9. – C. 867-870.
17. Егоров И.П. Эквиаффинные пространства третьей лакунарности / И.П. Егоров // ДАН СССР. – 1956. – Т. 103. – №1. – C. 151-152.
18. Кальницкий В.С. Полиномиальные симметрии плоских и однородных связностей / В.С. Кальницкий // Дифференциальная геометрия многообразий фигур. – 2004. – Т. 35.– С. 55-62.

Список литературы на английском языке / References in English

1. Postnikov M.M. Lekcii po geometrii. Gladkie mnogoobrazija. [Lectures on Geometry. Smooth Manifolds.] / M.M. Postnikov. – M.: Nauka. Gl. red. fiz.-mat. lit. – 1987. – p. 480 [in Russian]
2. Palais R. A global formulation of the Lie theory of transformation groups / R. Palais // Mem. Amer. Math. Soc. – 1957. – V. 22. – 123 p.
3. Kobayashi Sh. Osnovy differencial'nojj geometrii [Fundamentals of Differential Geometry, Vol. I] / Sh. Kobayashi , K.Nomizu . – M.: Nauka. – 1981. – p. 347 [in Russian]
4. Shevalle K. Teorija grupp Li [Theory of Lie Groups, T. I] / K. Shevalle. – M.: IL, 1948. [in Russian]
5. Postnikov M.M. Lekcii po geometrii. Gruppy i algebry Li. [Lectures on Geometry. Lie Groups and Algebras.] / M.M. Postnikov – M.: Nauka. Gl. red. fiz.-mat. lit. – 1982. – p. 447 [in Russian]
6. Kobayashi S., Transformation Groups in Differential Geometry / S. Kobayashi. – Springer-Verlag, New York. – 1972. – 190 P.
7. Kawski M. Geometric homogeneity and applications to stabilization / M. Kawski // Proc. IFAC Symp. NCSD. – 1995. – P. 147-152.
8. Crampin M. Applicable differential geometry / M. Crampin, F. A. E. Pirani // London Mathematical Society Lecture Notes Series 59. – Cambridge University Press. – 1986. –394 P.
9. Kal'nickijj V.S. Avtomorfizmy geodezicheskogo vektornogo polja [Automorphisms of a Geodesic Vector Field] / V.S. Kal'nickijj // Vestnik SPbGU [Bulletin of St. Petersburg State University], ser.1. – 1995. – Vol. 2, No.8. – p. 23-24. [in Russian]
10. Kal'nickijj V.S. Algebra obobshhennykh polejj Jakobi [Algebra of Generalized Jacobi Fields] / V.S. Kal'nickijj // Zap. nauch. sem. POMI, "Issledovanija po topologii" [Notes of Scientific Seminars of PDMI, "Research on Topology"], 8. – 1995. – Vol. 231. – pp. 222-243. [in Russian]
11. Kal'nickijj V.S. Polnota nil'potentnykh polejj [Completeness of Nilpotent Fields] / V.S. Kal'nickijj // Differencial'naja geometrija mnogoobrazijj figur [Differential Geometry of Manifolds of Figures]. – 2005. – Vol. 36.– pp. 50-53. [in Russian]
12. Stepanov S.E. Ob odnom primenenii teoremy Stoksa v global'nojj rimanovojj geometrii [On One Application of the Stokes Theorem in Global Riemannian Geometry] / S.E. Stepanov // Fund. i prikl. mat. [Fundamental and Applied Mathematics] Vol.8. – 2002. – No.1. – pp. 245-262. [in Russian]
13. Sasaki S. On the differential geometry of tangent bundle of Riemannian manifolds / S. Sasaki // Tôhoku Math. J. — 1958. — Vol. 10. — P. 338–354.
14. Kalnitsky V.S. Spray algebra / V.S. Kalnitsky // Proc. Math. Inst. NAS Ukr. – 2004. – V. 50, Part III. – P. 1356-1360.
15. Ashtekar A. A technique for analyzing the structure of isometries / A. Ashtekar, F. Magnon-Ashtekar // J. Math. Phys. – 1977. –V. 19. – P. 1567-1572.
16. Egorov I.P. O porjadke grupp dvizhenijj prostranstv affinnojj svjaznosti [On the Order of Groups of Movements of Spaces of Affine Connectivity] / I.P. Egorov // DAN SSSR [Proc. USSR Acad. Sci.]. – 1947. – Vol. 57. – No. 9. – pp. 867-870. [in Russian]
17. Egorov I.P. Ehkviaffinnye prostranstva tret'ejj lakunarnosti [Equiaffine Spaces of the Third Lacunarity] / I.P. Egorov // DAN SSSR [Proc. USSR Acad. Sci.]. – 1956. – Vol. 103. – No.1. – pp. 151-152. [in Russian]
18. Kal'nickijj V.S. Polinomial'nye simmetrii ploskikh i odnorodnykh svjaznostejj [Polynomial Symmetries of Plane and Homogeneous Connections] / V.S. Kal'nickijj // Differencial'naja geometrija mnogoobrazijj figur [Differential Geometry of Manifolds of Figures]. – 2004. – Vol. 35.– pp. 55-62. [in Russian]