ON NUMERICAL SOLUTION OF SYSTEMS OF LINEAR ALGEBRAIC EQUATIONS WITH ILL-CONDITIONED MATRICES
О ЧИСЛЕННОМ РЕШЕНИИ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ С ПЛОХО ОБУСЛОВЛЕННЫМИ МАТРИЦАМИ Научная статья Рябов В.М.1, Бурова И.Г.2, *, Кальницкая М.А.3, Малевич А.В.4, Лебедева А.В.5, Борзых А.Н.6
1 ORCID: 0000-0002-1364-5428; 2 ORCID: 0000-0002-8743-1377; 3 ORCID: 0000-0001-5671-5070; 4 ORCID: 0000-0003-0753-4621; 5 ORCID: 0000-0001-9026-0292; 6 ORCID: 0000-0001-5489-911X; 1, 2, 3, 4, 5, 6 Санкт-Петербургский государственный университет, Санкт-Петербург, Россия
* Корреспондирующий автор (i.g.burova[at]spbu.ru)
АннотацияПредставлены результаты численного решения систем линейных алгебраических уравнений (СЛАУ) с симметричными и несимметричными плохо обусловленными матрицами методом регуляризации. Рассматриваются положительно определенные, а также осцилляционные матрицы. В статье показано, что для регуляризации вычислительного процесса по методу Тихонова достаточно заменить матрицу An системы матрицей где ![]() – единичная матрица, а a – некоторое положительное число (параметр регуляризации), которое стремится к нулю.
– единичная матрица, а a – некоторое положительное число (параметр регуляризации), которое стремится к нулю.
Ключевые слова: плохо обусловленные системы линейных алгебраических уравнений, матрицы Гильберта, параметр регуляризации.
ON NUMERICAL SOLUTION OF SYSTEMS OF LINEAR ALGEBRAIC EQUATIONS WITH ILL-CONDITIONED MATRICES Research article Ryabov V.M.1, Burova I.G.2, *, Kalnitskaya M.A.3, Malevich A.V.4, Lebedeva A.V.5, Borzykh A.N.6
1 ORCID: 0000-0002-1364-5428; 2 ORCID: 0000-0002-8743-1377; 3 ORCID: 0000-0001-5671-5070; 4 ORCID: 0000-0003-0753-4621; 5 ORCID: 0000-0001-9026-0292; 6 ORCID: 0000-0001-5489-911X; 1, 2, 3, 4, 5, 6 St. Petersburg State University, St. Petersburg, Russia
* Corresponding author (i.g.burova[at]spbu.ru)
AbstractThe results of the numerical solution of systems of linear algebraic equations (SLAE) with symmetric and asymmetrical ill-conditioned matrices by the regularization method are presented in the paper. Positive-definite and oscillatory matrices are considered. The article shows that in order to regularize the computational process according to the Tikhonov method, it is enough to replace the system matrix A_n with the matrix A_n + αE_n where E_n is the identity matrix, and α is some positive number (regularization parameter) that tends to zero.
Keywords: ill-conditioned systems of linear algebraic equations, Hilbert matrices, regularization parameter.Введение
При решении различных задач возникает необходимость решать плохо обусловленные СЛАУ с положительно определенными симметричными матрицами. Такие системы линейных алгебраических уравнений возникают, например, когда функцию f (x) аппроксимируют алгебраическими многочленами в метрике пространства ![]() : если мы возьмем полином в виде
: если мы возьмем полином в виде ![]() и определим погрешность аппроксимации как
и определим погрешность аппроксимации как ![]()
![]() то из условия минимизации придем к СЛАУ с матрицей Гильберта. Такие системы линейных алгебраических уравнений также возникают при решении обыкновенных дифференциальных уравнений методом Ритца, что приводит к матрицам Грама. Эти матрицы размерности n являются симметричными и положительно определенными, но при неограниченном увеличении n наименьшее собственное значение может стремиться к нулю, что приводит к неустойчивости решения.
Обычно для получения надежного решения используют методы регуляризации. Общей стратегией является использование стабилизатора Тихонова [1] или его модификаций [2], [3], [4], [5], [6], [7]. В этой статье рассматриваются особенности численного решения СЛАУ с положительно определенной симметричной матрицей с использованием регуляризации. В следующих разделах показано, что для регуляризации вычислительного процесса по методу Тихонова достаточно заменить матрицу системы An матрицей
то из условия минимизации придем к СЛАУ с матрицей Гильберта. Такие системы линейных алгебраических уравнений также возникают при решении обыкновенных дифференциальных уравнений методом Ритца, что приводит к матрицам Грама. Эти матрицы размерности n являются симметричными и положительно определенными, но при неограниченном увеличении n наименьшее собственное значение может стремиться к нулю, что приводит к неустойчивости решения.
Обычно для получения надежного решения используют методы регуляризации. Общей стратегией является использование стабилизатора Тихонова [1] или его модификаций [2], [3], [4], [5], [6], [7]. В этой статье рассматриваются особенности численного решения СЛАУ с положительно определенной симметричной матрицей с использованием регуляризации. В следующих разделах показано, что для регуляризации вычислительного процесса по методу Тихонова достаточно заменить матрицу системы An матрицей ![]() , где En – единичная матрица, а α – положительное число (параметр регуляризации), стремящееся к нулю. Таким образом, мы уменьшаем число обусловленности системы линейных алгебраических уравнений, что увеличивает устойчивость.
Постановка задачи
Пусть A – невырожденная вещественная квадратная матрица порядка n. В этом случае решение СЛАУ Az = f существует и единственно. Известны различные модификации метода Гаусса для решения СЛАУ, например, метод Гаусса с выбором ведущего элемента (в столбце или в матрице) и другие. Предположим, что число обусловленности
, где En – единичная матрица, а α – положительное число (параметр регуляризации), стремящееся к нулю. Таким образом, мы уменьшаем число обусловленности системы линейных алгебраических уравнений, что увеличивает устойчивость.
Постановка задачи
Пусть A – невырожденная вещественная квадратная матрица порядка n. В этом случае решение СЛАУ Az = f существует и единственно. Известны различные модификации метода Гаусса для решения СЛАУ, например, метод Гаусса с выбором ведущего элемента (в столбце или в матрице) и другие. Предположим, что число обусловленности ![]() матрицы A велико, т.е. матрица системы уравнений плохо обусловлена. Решение плохо обусловленных СЛАУ методом Гаусса не всегда дает удовлетворительное решение. Например, пусть
матрицы A велико, т.е. матрица системы уравнений плохо обусловлена. Решение плохо обусловленных СЛАУ методом Гаусса не всегда дает удовлетворительное решение. Например, пусть
![]() Число обусловленности матрицы A приближенно равно 107 . Решая эту систему методом Гаусса без перестановок (с помощью программы, написанной на C++ с вещественными числами типа double), получим z = (1.0? 1.555556, 0.666667)T , что существенно отличается от точного решения (1.0, 1.0, 1.0)T. Подобные примеры были рассмотрены в [6]. Эти примеры показывают, что в процессе решения необходимо избегать деления на малые по абсолютной величине элементы. Избежать эту ситуацию помогает использование модифицированного метода Гаусса, заключающегося в выборе ведущего элемента, являющегося наибольшим по абсолютному значению элементом в столбце (стратегия Уилкинсона) или по всей матрице (стратегия полного упорядочения Жордана) [2]. Применение метода Гаусса с выбором ведущего элемента по столбцам дает решение z = (1.0, 1.0., 1.0)T. Если система уравнений является плохо обусловленной, например, в случае СЛАУ с матрицей Гильберта
Число обусловленности матрицы A приближенно равно 107 . Решая эту систему методом Гаусса без перестановок (с помощью программы, написанной на C++ с вещественными числами типа double), получим z = (1.0? 1.555556, 0.666667)T , что существенно отличается от точного решения (1.0, 1.0, 1.0)T. Подобные примеры были рассмотрены в [6]. Эти примеры показывают, что в процессе решения необходимо избегать деления на малые по абсолютной величине элементы. Избежать эту ситуацию помогает использование модифицированного метода Гаусса, заключающегося в выборе ведущего элемента, являющегося наибольшим по абсолютному значению элементом в столбце (стратегия Уилкинсона) или по всей матрице (стратегия полного упорядочения Жордана) [2]. Применение метода Гаусса с выбором ведущего элемента по столбцам дает решение z = (1.0, 1.0., 1.0)T. Если система уравнений является плохо обусловленной, например, в случае СЛАУ с матрицей Гильберта ![]() порядка n с элементами
порядка n с элементами ![]() , то практически невозможно получить приемлемое решение СЛАУ с помощью известных методов (прямыми методами, такими как метод Гаусса, метод квадратного корня, итерационными методами и др.).
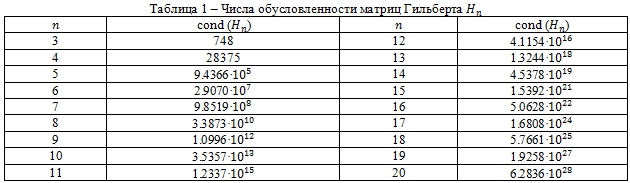
В таблице 1 приведены числа обусловленности матриц Гильберта порядков от 3 до 20, полученные с помощью пакета Maple (Digits=50). В таблице 2 представлены решения СЛАУ Az = f c матрицами Гильберта Hn, полученные методом Гаусса (стратегия Уилкинсона). Здесь представлены решения, полученные при решении систем уравнений для n= 10, 12, 14, 20, вычисленные в C++ с числами типа double. Решения, представленные в таблице 2, далеки от истинных решений. В следующих разделах представлен метод регуляризации, с помощью которого получены решения исходной системы Az = f с матрицами Гильберта A = Hn при использовании нормы
, то практически невозможно получить приемлемое решение СЛАУ с помощью известных методов (прямыми методами, такими как метод Гаусса, метод квадратного корня, итерационными методами и др.).
В таблице 1 приведены числа обусловленности матриц Гильберта порядков от 3 до 20, полученные с помощью пакета Maple (Digits=50). В таблице 2 представлены решения СЛАУ Az = f c матрицами Гильберта Hn, полученные методом Гаусса (стратегия Уилкинсона). Здесь представлены решения, полученные при решении систем уравнений для n= 10, 12, 14, 20, вычисленные в C++ с числами типа double. Решения, представленные в таблице 2, далеки от истинных решений. В следующих разделах представлен метод регуляризации, с помощью которого получены решения исходной системы Az = f с матрицами Гильберта A = Hn при использовании нормы
![]()

Численное решение плохо обусловленной системы уравнений
Различные подходы к решению систем уравнений с плохо обусловленными матрицами известны (см. [1-7]). В данной работе для получения приемлемого решения СЛАУ рассматривается применение модификации метода регуляризации. Известный стандартный метод регуляризации Тихонова позволяет найти нормальное решение системы Az = f. Этот метод основан на поиске элемента, на котором функционал ![]()
![]() достигает наименьшего значения для фиксированного положительного Для этого необходимо решить уравнение Эйлера
достигает наименьшего значения для фиксированного положительного Для этого необходимо решить уравнение Эйлера![]() - сопряженная матрица. Решение уравнения Эйлера зависит от числа обусловленности матрицы A*A . Это число может быть очень большим. Если матрица A симметрична и положительно определена, мы предлагаем найти нормальное решение другим способом. В данной работе предлагается найти нормальное решение путем решения системы уравнений, для которой число обусловленности значительно меньше.
Пусть матрица СЛАУ
- сопряженная матрица. Решение уравнения Эйлера зависит от числа обусловленности матрицы A*A . Это число может быть очень большим. Если матрица A симметрична и положительно определена, мы предлагаем найти нормальное решение другим способом. В данной работе предлагается найти нормальное решение путем решения системы уравнений, для которой число обусловленности значительно меньше.
Пусть матрица СЛАУ
|
Az=f |
(1) |
является симметричной и положительно определенной (например, матрица Гильберта). В этом случае существует единственный положительно определенный корень из матрицы , т.е. положительно определенная матрица такая, что . Установим связь между собственными значениями и собственными векторами матриц и : пусть µ и собственное значение и собственный вектор матрицы :
|
B=µx |
(2) |
|
Ax=µBx |
(3) |
Используя (2), перепишем (3) как ![]() . Это равенство означает, что собственные векторы матриц A и B одинаковы, а собственные значения матрицы A равны квадратам собственных значений матрицы B. Умножив (1) на , получаем
. Это равенство означает, что собственные векторы матриц A и B одинаковы, а собственные значения матрицы A равны квадратам собственных значений матрицы B. Умножив (1) на , получаем
|
𝐵𝑧=B-1 𝑓 |
(4) |
Запишем для (4) уравнение Эйлера для минимизации сглаживающего функционала![]()
![]() : оно имеет вид
: оно имеет вид
|
(B*B+αE)za=B*(B-1f), a>0 |
(5) |
В случае симметричной матрицы матрица является самосопряженной, поэтому мы получаем уравнение
|
(A+αE) Zα=f |
(6) |
Формально в исходной системе осуществляется сдвиг, но фактически это метод регуляризации для уравнения (1).
В памяти компьютера числа обычно хранятся с некоторыми погрешностями. Будем считать, что матрица и вектор даны приближенно, т.е. вместо матрицы A и правой части ![]() известны
известны ![]() такие, что
такие, что ![]() δ. Говорить о сходимости можно лишь при неограниченном увеличении точности исходной информации, т.е. при δ→0. Однако практически мы не можем неограниченно уменьшать δ, из-за чего результаты могут быть далеки от желаемых решений. Решая задачу (6), получаем приближенное решение системы (1).
Замечание. Методы вычисления квадратного корня матрицы описаны в [8-11]. Если матрица A симметрична, нам не нужно вычислять матрицу B. Применение регуляризации непосредственно к уравнению (1) просто увеличит число обусловленности результирующей системы, что невыгодно. В случае несимметричной положительно определенной матрицы уравнение Эйлера для системы (1) имеет вид (5). Сходимость метода регуляризации изложена в [1]. В отличие от стандартного подхода процедуры регуляризации представление (5) имеет меньшее число обусловленности, что очень важно. Но, в отличие от симметричных матриц, необходимо знать матрицу B в случае несимметричной матрицы. Последнее требование усложняет применение данного метода на практике.
Существуют классы несимметричных матриц, все собственные значения которых положительны. Покажем, как в этом случае можно осуществить процесс регуляризации в форме (5), а не в традиционной форме
δ. Говорить о сходимости можно лишь при неограниченном увеличении точности исходной информации, т.е. при δ→0. Однако практически мы не можем неограниченно уменьшать δ, из-за чего результаты могут быть далеки от желаемых решений. Решая задачу (6), получаем приближенное решение системы (1).
Замечание. Методы вычисления квадратного корня матрицы описаны в [8-11]. Если матрица A симметрична, нам не нужно вычислять матрицу B. Применение регуляризации непосредственно к уравнению (1) просто увеличит число обусловленности результирующей системы, что невыгодно. В случае несимметричной положительно определенной матрицы уравнение Эйлера для системы (1) имеет вид (5). Сходимость метода регуляризации изложена в [1]. В отличие от стандартного подхода процедуры регуляризации представление (5) имеет меньшее число обусловленности, что очень важно. Но, в отличие от симметричных матриц, необходимо знать матрицу B в случае несимметричной матрицы. Последнее требование усложняет применение данного метода на практике.
Существуют классы несимметричных матриц, все собственные значения которых положительны. Покажем, как в этом случае можно осуществить процесс регуляризации в форме (5), а не в традиционной форме ![]() что, как уже упоминалось выше, существенно уменьшает число обусловленности решаемой системы. Рассматривается класс осцилляционных матриц (см. [12]), все собственные значения которых положительны и попарно различны, а соответствующие собственные векторы обладают особыми свойствами колебаний.
Пусть матрица An - осцилляционная, а V есть матрица собственных векторов
что, как уже упоминалось выше, существенно уменьшает число обусловленности решаемой системы. Рассматривается класс осцилляционных матриц (см. [12]), все собственные значения которых положительны и попарно различны, а соответствующие собственные векторы обладают особыми свойствами колебаний.
Пусть матрица An - осцилляционная, а V есть матрица собственных векторов ![]() - диагональная матрица собственных чисел An. Тогда
- диагональная матрица собственных чисел An. Тогда ![]() Пусть
Пусть ![]() . Положим
. Положим ![]() Понятно, что
Понятно, что ![]() Таким образом, процесс регуляризации может быть осуществлен в форме (5). Обобщенная матрица Вандермонда, то есть матрица вида
Таким образом, процесс регуляризации может быть осуществлен в форме (5). Обобщенная матрица Вандермонда, то есть матрица вида ![]() ... < bn, относится к классу осцилляционных матриц. Для регуляризации СЛАУ с такими матрицами применима описанная выше схема.
Результаты применения метода регуляризации
Проведена серия вычислительных экспериментов по применению метода регуляризации для решения СЛАУ с матрицами Гильберта порядков n=2,3,...,20. В таблицах 3, 4 показаны результаты применения метода регуляризации для различных параметров a = 10-1, 10-2,..., 10-12 для решения возмущенной СЛАУ
... < bn, относится к классу осцилляционных матриц. Для регуляризации СЛАУ с такими матрицами применима описанная выше схема.
Результаты применения метода регуляризации
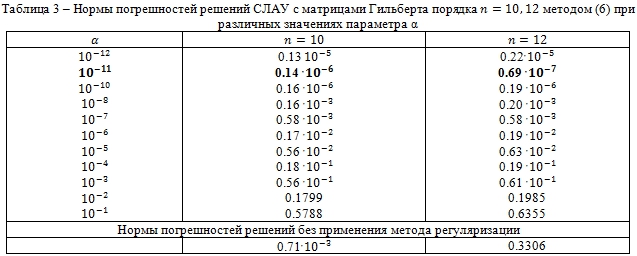
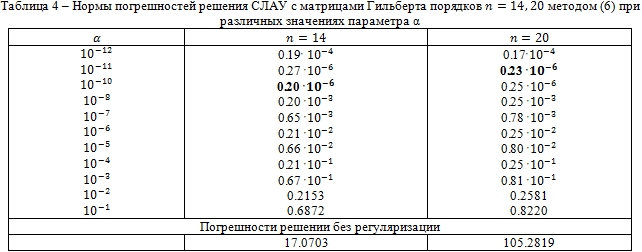
Проведена серия вычислительных экспериментов по применению метода регуляризации для решения СЛАУ с матрицами Гильберта порядков n=2,3,...,20. В таблицах 3, 4 показаны результаты применения метода регуляризации для различных параметров a = 10-1, 10-2,..., 10-12 для решения возмущенной СЛАУ ![]() где матрица исходной системы
где матрица исходной системы ![]() есть матрица Гильберта порядка n. Решение возмущенной системы получено методом Гаусса с выбором ведущего элемента по столбцам. Точное решение исходной невозмущенной системы Hnz = f есть n-мерный вектор из единиц: z = (1.0, 1.0, ..., 1.0)T. Вычисляя решение возмущенной СЛАУ при различных значениях α, находим значение параметра, при котором погрешность решения имеет минимальное значение. Параметр α, соответствующий решению с наименьшей нормой, назовем оптимальным. Таким образом, для решения системы уравнений (1) необходимо решить несколько систем уравнений для различных α. В таблицах 3, 4 полужирным шрифтом выделено наименьшее значение нормы погрешности для заданного n, соответствующее оптимальному значению параметра возмущения α. В последней строке этих таблиц приведены нормы погрешностей решений, полученных без регуляризации. Погрешность решения вычислялась с помощью евклидовой нормы.
есть матрица Гильберта порядка n. Решение возмущенной системы получено методом Гаусса с выбором ведущего элемента по столбцам. Точное решение исходной невозмущенной системы Hnz = f есть n-мерный вектор из единиц: z = (1.0, 1.0, ..., 1.0)T. Вычисляя решение возмущенной СЛАУ при различных значениях α, находим значение параметра, при котором погрешность решения имеет минимальное значение. Параметр α, соответствующий решению с наименьшей нормой, назовем оптимальным. Таким образом, для решения системы уравнений (1) необходимо решить несколько систем уравнений для различных α. В таблицах 3, 4 полужирным шрифтом выделено наименьшее значение нормы погрешности для заданного n, соответствующее оптимальному значению параметра возмущения α. В последней строке этих таблиц приведены нормы погрешностей решений, полученных без регуляризации. Погрешность решения вычислялась с помощью евклидовой нормы.
Точность арифметики с плавающей запятой можно охарактеризовать машинным ε, т.е. наименьшим положительным числом с плавающей запятой ε, для которого 1 + ε >1 (см. [6]). Мы можем вычислить машинное ε. Например, в 64-битном С++ переменные типа double дают ![]()
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы / References
- Тихонов А. Н. Методы решения некорректных задач / А. Н. Тихонов, В. Я. Арсенин. – М.: Наука. Главная редакция физико-математической литературы, 1979. Изд. 2-е. – 284 с.
- Фаддеев Д. К. Вычислительные методы линейной алгебры / Д. К. Фаддеев, В. Н. Фаддеева. – М.: Физматгиз, 1960. – 656 с.
- Фаддеев Д.К. О плохо-обусловленных системах линейных уравнений / Д. К. Фаддеев, В. Н. Фаддеева // Журнал вычислительной математики и математической физики. – 1961. – Т. 1. – №3. – С. 412–417.
- Гавурин М.К. О плохо-обусловленных системах линейных алгебраических уравнений / М. К. Гавурин // Журнал вычислительной математики и математической физики. – 1962. – Т. 2. – №3. – С. 387–397.
- Гавурин М. К. Применение полиномов Чебышева при регуляризации некорректных и плохо обусловленных уравнений в гильбертовом пространстве / М. К. Гавурин, В. М. Рябов // Журнал вычислительной математики и математической физики. – 1973. – Т. 13. – №6. – С. 1599–1601.
- Форсайт Дж. Численное решение систем линейных алгебраических уравнений / Дж. Форсайт, К. Молер. Перевод с английского В.П. Ильина и Ю.И. Кузнецова. Под редакцией Г.И. Марчука. – М.: Мир, 1969. – 167 с.
- Кабанихин С. И. Обратные и некорректные задачи / С.И. Кабанихин. – Новосибирск: Сибирское научное издательство, 2009. – 457с.
- Bjorck A. A Schur method for the square root of a matrix / A. Bjorck, S. Hammarling // Linear Algebra Appl. – 1983. – V. 52/53, P. 127–140.
- Higham Nicholas J. Functions of matrices: Theory and computation / J. Higham Nicholas – Philadelphia: Society for Industrial and Applied Mathematics, 2008. – 425 p.
- Deadman E. Blocked Schur algorithms for computing the matrix square root / E. Deadman, N.J. Higham, R. Ralha // Lecture Notes in Computer Science, V. 7782, Springer-Verlag. – 2012. P. 171–182.
- Higham Nicholas J. Newton's Method for the Matrix Square Root / J. Higham Nicholas // Mathematics of computation. – 1986. – V. 46. – №174. – P. 537–549.
- Гантмахер Ф. Р. Осцилляционные матрицы и ядра и малые колебания механических систем / Ф.Р. Гантмахер, М.Г. Крейн // Москва-Ленинград: Государственное издательство технико-теоретической литературы [ГИТТЛ], 1950. 359 с.
