ON SOME ISSUES OF INTEGRATION IN MULTIDIMENSIONAL SPACES
Мирошников А.Л.1, Миллер Н.В.2, Попова Н.И.3, Швец Ю.В.4
1ORCID: 0000-0001-6057-0919, кандидат физико-математических наук,
2ORCID: 0000-0002-9351-6123, кандидат педагогических наук,
3ORCID: 0000-0002-2186-3556, кандидат педагогических наук,
4ORCID: 0000-0002-6742-070X, кандидат педагогических наук,
Сибирский государственный университет путей сообщения, г. Новосибирск
О НЕКОТОРЫХ ВОПРОСАХ ИНТЕГРИРОВАНИЯ В МНОГОМЕРНЫХ ПРОСТРАНСТВАХ
Аннотация
Работа посвящена установлению различных нетривиальных оценок функции концентрации. Интерес к этой функции связан с тем, что она является важнейшим инструментом для изучения свойств сверсток различных вероятностных распределений, которые появляются в многочисленных приложениях. В представленной статье обобщаются на многомерные пространства некоторые результаты, полученные для этой функции в одномерном случае. Так, в работе усиливается (см. теорему 2) известный результат Энгера из работы [1]. Кроме того, показывается, что оценка из теоремы 2 является неулучшаемой по размерности пространства. Доказательства основных результатов основаны на использовании метода характеристических функций. Основная трудность связана с оценками сложных многомерных интегралов.
Ключевые слова: многомерные пространства, функция концентрации, оценки функции концентрации, выпуклый функционал, интегрирование в многомерных пространствах.
Miroshnikov A.L.1, Miller N.V.2, Popova N.I.3, Shvets Yu.V.4
1ORCID: 00010-0001-6057-0919, PhD in Physics and Mathematics, 2ORCID: 0000-0002-9351-6123, PhD in Pedagogy, 3ORCID: 0000-0002-2186-3556, PhD in Pedagogy, 4ORCID: 0000-0002-6742-070X, PhD in Pedagogy,
Siberian State Transport University, Novosibirsk
ON SOME ISSUES OF INTEGRATION IN MULTIDIMENSIONAL SPACES
Abstract
The paper is devoted to founding of various nontrivial estimates of the concentration function. The interest in this function is due to the fact that it is the most important tool for studying the properties of the convolutions of various probability distributions that appear in numerous applications. Some results obtained for this function in the one-dimensional case are generalized to multidimensional spaces in the presented paper. Thus, the well-known result of Enger from [1] is strengthened (see Theorem 2). In addition, it is shown that the estimate in Theorem 2 is unimprovable in the dimension of the space. The proofs of the main results are based on the use of the method of characteristic functions. The main difficulty is connected with the estimates of complex multidimensional integrals.
Keywords: multidimensional spaces, concentration function, estimates of the concentration function, convex functional, integration in multidimensional spaces.
Математическое моделирование реальных процессов и явлений является одним из самых эффективных методов исследования действительности, включающих в себя создание математической модели, нахождение и исследование решения модельной задачи, сравнение полученных решений с реальностью, корректировку модели по адекватности, использование уточненной модели для исследования целого класса реальных явлений.
Еще в первой половине XX века появилась знаменитая монография Леви [2, P.36], в которой была определена специальная характеристика вероятностного распределения – функция концентрации, которая стала важным инструментом изучения свойств сверток распределений. В дальнейшем, функция концентрации Леви исследовалась в работах А.Н. Колмогорова, Б.А. Рогозина, В.В. Сазонова, В.В. Петрова, А.Б. Мухина, А.А. Юдина, Н.Г. Ушакова, К. Эссеена, Х. Кестена, Я. Энгера и в наше время нашла применение в исследованиях А.Ю. Зайцева, Ф. Гётце, В.В. Ульянова и других отечественных и зарубежных математиков. Данной теме посвящена монография В. Хенгартнера и Р. Теодореску [3] и недавние работы отечественных ученых [10], [11], [12].
Функция концентрации Леви (или просто функция концентрации) суммы независимых случайных величин в одномерном случае исследована достаточно глубоко. Для нее получены неулучшаемые в общем случае оценки. Однако в случае многомерного пространства остались нерешенные вопросы. Так, еще не описан полностью класс множеств, для которых получаются неравенства с абсолютной постоянной, что необходимо для обобщения оценок на гильбертово пространство.
Формулировка основных результатов
Многомерная функция концентрации Леви ![]() , где ξ - случайный вектор, а Е – выпуклое множество в
, где ξ - случайный вектор, а Е – выпуклое множество в ![]() , определяется равенством:
, определяется равенством:
![]()
где Р – вероятность.
Пусть ![]() ,
, ![]() , тогда
, тогда ![]() ;
; ![]() .
.
Обозначим ![]() ,
,
где ![]() – ортонормированный базис в
– ортонормированный базис в ![]() .
.
Отметим, что E является симметричным выпуклым множеством, а выпуклый функционал ![]() – функционалом Минковского для куба Е.
– функционалом Минковского для куба Е.
Пусть ![]() – последовательность независимых случайных векторов в
– последовательность независимых случайных векторов в ![]() ;
; ![]() .
.
Положим ![]() .
.
Под вектором ξ будем понимать вектор![]() , у которого
, у которого ![]() независимы и одинаково распределены с ξ, и если P(∙) – распределение случайного вектора , то
независимы и одинаково распределены с ξ, и если P(∙) – распределение случайного вектора , то ![]() – распределение случайного вектора ξ.
– распределение случайного вектора ξ.
В [1, С. 17] получены следующие неравенства:
![]() (1)
(1)
![]() (2)
(2)
где Е – d –мерный куб, М – математическое ожидание. Здесь и далее С – абсолютная постоянная.
Как следует из [1], зависимость от размерности в правой части (2) существенна. Действительно, если бы имели для d – мерного куба оценку вида (1), т.е. без размерности d в правой части, то пришли бы к противоречию. Для этого достаточно взять за ![]() (n = d) последовательность независимых случайных векторов в
(n = d) последовательность независимых случайных векторов в ![]() , таких что
, таких что
![]()
Тогда ![]() и
и 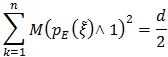 .
.
Подставив данные равенства в (2) получим оценку ![]() , что заведомо приводит к противоречию при больших d.
, что заведомо приводит к противоречию при больших d.
Теорема 1. Если ![]() независимые случайные векторы, то
независимые случайные векторы, то
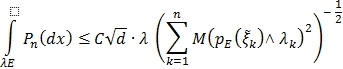
Теорема 2. Если ![]() – независимые случайные векторы, то
– независимые случайные векторы, то
![]() (3)
(3)
Заметим, что: из (3) следует (2); оценка (3) по d неулучшаема, что следует из приведенного выше примера; оценка (3) точнее оценки (2) в том смысле, что она дает более точное неравенство функции концентрации суммы, когда ![]() мал.
мал.
Доказательство основных результатов
Доказательство теоремы 1
Имеем:
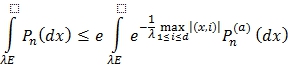
где ![]() - распределение
- распределение ![]() .
.
Заметим, что
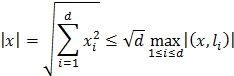
и, следовательно, 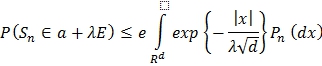 .
.
Но ![]() есть характеристическая функция некоторой вероятностной меры μ(∙) [1] , т.е.
есть характеристическая функция некоторой вероятностной меры μ(∙) [1] , т.е. ![]() .
.
Отсюда:
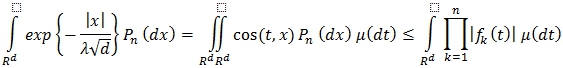
где ![]() – характеристическая функция
– характеристическая функция ![]() . Итак, имеем:
. Итак, имеем:
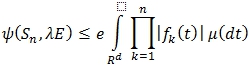 (4)
(4)
где μ(∙) - вероятностная мера с характеристической функцией ![]() .
.
Интеграл, стоящий в правой части равенства (4), оценим по методу, изложенному в . Вариацию этого метода можно найти у Зингеля .
Имеем
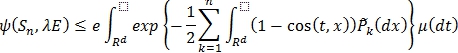
где ![]() - распределение вектора
- распределение вектора ![]() .
.
Пусть 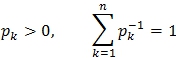 , тогда по неравенству Гельдера:
, тогда по неравенству Гельдера:
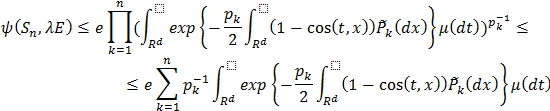
Обозначим:
![]()
Выберем ![]() , где
, где
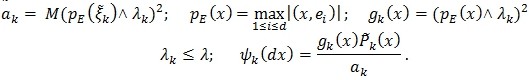
Тогда:
![]()
По неравенству Иенсена:
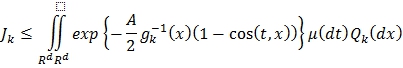
Рассмотрим интеграл
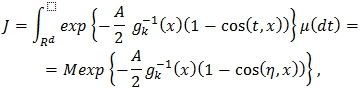
где вектор η имеет характеристическую функцию ![]() . Найдем характеристическую функцию случайной величины
. Найдем характеристическую функцию случайной величины ![]() .
.
Возьмем ![]() и рассмотрим
и рассмотрим
![]()
Отсюда величина (η, χ) имеет распределение Коши с плотностью
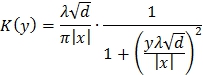 .
.
Тогда
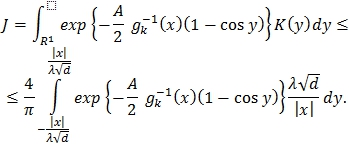
Неравенство следует из свойств распределения Коши. Далее имеем:
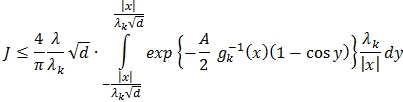
Очевидно, ![]() .
.
Следовательно,
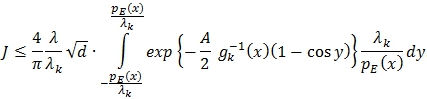
Тогда, получим:
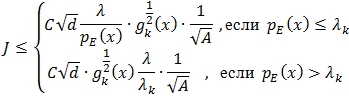
Таким образом,
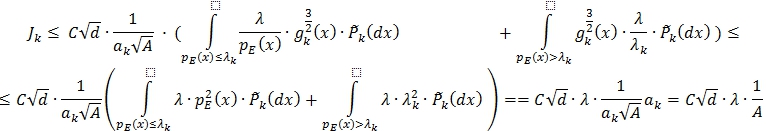
Отсюда
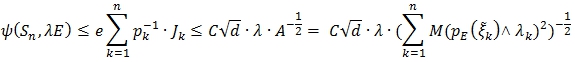
Теорема 1 доказана.
Доказательство теоремы 2
Если ![]() , то (3) следует из теоремы 1, а если
, то (3) следует из теоремы 1, а если ![]() , то (3) тривиально. Допустим
, то (3) тривиально. Допустим ![]() и
и ![]() .
.
Возьмем некоторое ![]() такое что:
такое что:
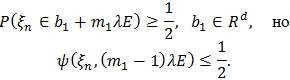
Без ограничения общности будем считать, что
![]()
Обозначим за ![]() событие
событие ![]() – дополнение к
– дополнение к ![]() ;
;
![]()
Возьмем произвольное ![]() , тогда:
, тогда:
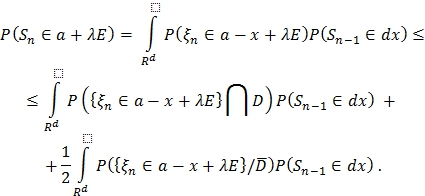
Заметим, что ![]() , если
, если ![]()
Следовательно,
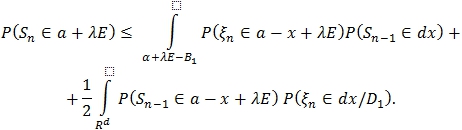
Таким образом:
![]()
Но ![]() , и мы получаем неравенство:
, и мы получаем неравенство:
![]()
Согласно теореме 1:
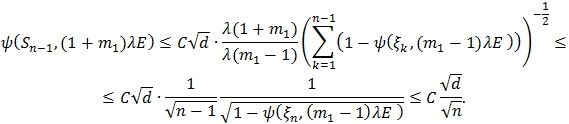
Окончательно имеем:
![]()
Далее, существует ![]() , такое что:
, такое что:
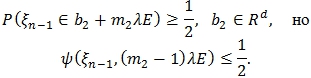
И можно считать, что ![]() такой вектор, что:
такой вектор, что:
![]()
Обозначим за ![]() событие
событие ![]() .
.
Применяя описанный выше метод для оценки ![]() , получим:
, получим:
![]()
Теперь оцениваем ![]() и так далее. Через
и так далее. Через ![]() шага мы приходим к неравенству
шага мы приходим к неравенству
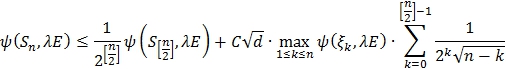
Заметим, что:
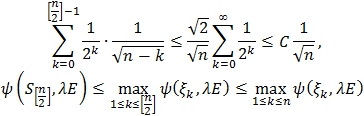
Отсюда ![]()
Следовательно,
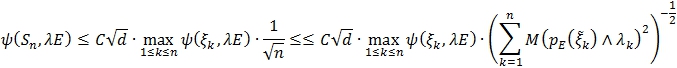
Теорема 2 доказана.
Список литературы / References
- Enger J. Bounds for the concentration function of a sum of independent random vectors with values in a Euclidean or Hilbert space / J. Enger. – Uppsala: Thesis Uppsala University, 1975. - 68 p.
- Levy P. Theorie de I΄addition des variables aletorires / P. Levy. - Paris: Gauthier – Villar, 1937. - 228 p.
- Хенгартер В., Теодореску Р. Функции концентрации / В. Хенгартер, Р. Теодореску. - М.: Наука, 1980. - 176 с.
- Зигель Г. Верхние оценки для функции концентрации в гильбертовом пространстве / Г. Зигель // Теория вероятностей и ее применение. Т. 26. – 1981. - С. 335-34.
- Гётце Ф., Зайцев А.Ю. Оценки точности сильной аппроксимации в гильбертовом пространстве / Ф. Гётце, А. Ю. Зайцев // Сиб. матем. Журнал. – 2011. - №52:4. - С. 796-808.
- Мирошников А.Л., Рогозин Б.А. Неравенства для функции концентрации / А. Л. Мирошников, Б. А. Рогозин // Теория вероятностей и ее применение. Т. 25, в.1. – 1980. - С. 178-183.
- Ананевский С.М., Мирошников А.Л. Локальные оценки функции концентрации Леви в многомерном гильбертовском пространстве / С. М. Ананевский, А. Л. Мирошников // Записки научных семинаров ЛОМИ. Т. 130 – 1983. - С. 6-11.
- Мирошников А.Л. Локальная оценка многомерной функции концентрации Леви для куба / А.Л. Мирошников // IV Международная Вильнюсская конференция по теории вероятностей и математической статистике. Тезисы докладов. Т. II / Ин-т математики и кибернетики АН Лит. ССР. – Вильнюс. 1985. – С. 192.
- Tao T., Van. V. From the Littlewood–Offord problem to the circular law: universality of the spectral distribution of random matrices / T. Tao, V. Van // Bull. Amer. Math. Soc. - 2009. - Vol. 46 (3). - P. 377–396
- Елисеева Ю.С., Зайцев А. Ю. Оценки функций концентрации взвешенных сумм независимых одинаково распределенных случайных величин / Ю. С. Елисеева, А. Ю. Зайцев // Теория вероятностей и ее применение. Т. 57. – 2012. - C. 768–777.
- Елисеева Ю.С. Многомерные оценки функций концентрации взвешенных сумм независимых одинаково распределенных случайных величин / Ю. С. Елисеева // Зап. науч. семинар / ПОМИ. - 2013. - 127–137.
- Vershynin R. Invertibility of symmetric random matrices / R. Vershynin // Random Structures and Algorithms. - 2014. - Vol. 44. - P. 135–182
Список литературы на английском языке / References in English
- 1. Enger J. Bounds for the concentration function of Euclidean or Hilbert space / J. Enger. - Uppsala: Thesis Uppsala University, 1975. - 68 p.
- Levy P. Theorie de Iaddition des variables aletorires / P. Levy. - Paris: Gauthier - Villar, 1937. - 228 p.
- Hengarter V., Teodorescu R. Funktsii kontsentratsii [Concentration Functions] / V. Hengarter, R. Theodorescu. - Moscow: Nauka, 1980. - 176 p. [in Russian]
- Siegel, G., Verkhniye otsenki dlia funktsi kontsentratsii v gilbertovom prostranstve [Upper Bounds for Concentration Function in Hilbert Space] // Probability theory and its application. Vol. 26. - 1981. - P. 335-34. [in Russian]
- Götze F., Zaitsev A. Yu. Otsenki tochnosti silnoy approksimatsii v gilbertovom prostranstve [Accuracy Estimates of Strong Approximation in Hilbert Space] / F. Götze, A. Yu. Zaitsev // Sibirsk. Math. Journal. - 2011. - No. 52: 4. - P. 796-808. [in Russian]
- Miroshnikov A.L., Rogozin B.A. Neravenstva dlia funktsii kontsentratsii [Inequalities for Concentration Function] / A.L. Miroshnikov, B.A. Rogozin // Theory of Probability and its Application. Vol. 25, p.1. - 1980. - P. 178-183. [in Russian]
- Ananevsky S.M., Miroshnikov A.L. Lokalniye otsenki funktsii kontsentratsii Levi v mnogomernom gilbertovom prostranstve [Local Estimates of Levi Concentration Function in Multidimensional Hilbert Space] / S.M. Ananevskii, A.L. Miroshnikov // Zapiski sovetnikov Seminam LOMI. Vol. 130 - 1983. - P. 6-11. [in Russian]
- Miroshnikov A.L. Lokalnaya otsenka mnogomernoy funktsii kontsentratsii Levi dlia kuba [Local Estimate of Multidimensional Levi Concentration Function for Cube] / A.L. Miroshnikov // IV International Vilnius Conference on Probability Theory and Mathematical Statistics. Theses of reports. T. II / Institute of Mathematics and Cybernetics of the Academy of Sciences of Lithuania. SSR. - Vilnius. 1985. - P. 192. [in Russian]
- Tao T., Van. V. From the Littlewood-O ff ord problem to the circular law: universality of the spectral distribution of random matrices / T. Tao, V. Van // Bull. Amer. Math. Soc. - 2009. - Vol. 46 (3). - P. 377-396.
- Eliseeva Yu. S., Zaitsev A. Yu. Otsenki funktsiy kontsentratsii vzveshennikh summ nezavisimykh odinakovo raspredelennykh sluchaynikh velechin [Estimates of Concentration Functions of Weighted Sums of Independent Identically Distributed Random Variables] Yu. S. Eliseeva, A. Yu. Zaitsev // Theory of Probability and its Application. Vol. 57. - 2012. - P. 768-777. [in Russian]
- Yu. S. Eliseeva, Mnogomerniye otsenki funktsiy kontsentratsii vzveshennykh summ nezavisimykh odinakovo raspredelennykh sluchaynikh velichin [Multidimensional estimates for the concentration functions of weighted sums of independent identically distributed random variables] Yu. S. Eliseeva, Zap. sci. seminar / SEM. - 2013. - P. 127-137. [in Russian]
- Vershynin R. Invertibility of symmetric random matrices / R. Vershynin // Random Structures and Algorithms. 2014. Vol. 44.-P. 135-182.
