MATHEMATICAL MODEL OF LEUKEMIA
Абузярова Р.Т.1, Колпак Е.П.2
1ORCID: 0000-0002-3694-7832, студент,
2ORCID: 0000-0001-6956-4814, доктор физико-математических наук,
Санкт-Петербургский государственный университет
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ЛЕЙКОЗА
Аннотация
Разработана математическая модель лейкоза на основании современных данных о кроветворении у млекопитающих. В модели рассматриваются три типа клеток, один из которых лейкозные. Взаимодействие клеток рассматривается как конкуренция за функциональное пространство делящихся клеток. За лейкозные клетки принимаются клетки, делящиеся с большей скоростью, чем все остальные. Модель замены лейкозных клеток клетками донора рассматривается как внедрение более активных клеток, чем лейкозные. Модель представлена задачей Коши для системы обыкновенных дифференциальных уравнений. Нарушение функций кроветворения сопоставляется с изменением ведущего параметра, переводящего систему из устойчивого стационарного состояния в неустойчивое.
Ключевые слова: лейкоз, математическое моделирование, устойчивость, дифференциальные уравнения, задача Коши, стационарная точка.
Abuzyarova R.T.1, Kolpak E.P.2
1ORCID: 0000-0002-3694-7832, Student,
2ORCID: 0000-0001-6956-4814, PhD in Physics and Mathematics,
St. Petersburg State University
MATHEMATICAL MODEL OF LEUKEMIA
Abstract
We developed a mathematical model of leukemia on the basis of modern data on hematopoiesis in mammals. Three types of cells are considered in the model, one of which is leukemia. Interaction of cells is studied as a competition for the functional space of dividing cells. Leukemia cells are cells dividing at a higher rate than all the others. The model of replacement of leukemic cells with donor cells is considered as the introduction of more active cells than leukemia ones. The model is represented by the Cauchy problem for a system of ordinary differential equations. Violation of hematopoiesis functions is correlated with a change in the leading parameter, which transfers the system from a stable steady state to an unstable one.
Keywords: leukemia, mathematical modeling, stability, differential equations, Cauchy problem, stationary point.
Введение
Одним из острых заболеваний является лейкоз. Ему подвержены все возрастные группы. Это заболевание трудноизлечимо, и может длиться, несмотря на лечение, годами. Очень высок процент летальных исходов. Болезнь протекает с осложнениями. Наиболее распространенным и дорогостоящим методом лечения является пересадка в больной организм донорского костного мозга. Однако чужеродные клетки начинает отторгать иммунная система и, в результате, выход в ремиссию часто сопровождается другими заболеваниями организма. Лечение осуществляется и введением в больной организм препаратов, помогающих справиться с заболеванием. Стоимость лечения препаратами составляет около 100 средних по России месячных зарплат. При благоприятном исходе лечения выход в ремиссию не означает, что не возникнет рецидив. Математическое моделирование лейкоза и вариантов его лечения могут помочь лечащим заболевание специалистам спланировать лечение и по его срокам и по его стоимости.
Кровотечение
Кроветворение – это процесс образования тромбоцитов, эритроцитов и лейкоцитов. Родоначальными клетками гемопоэза являются стволовые клетки (СК), благодаря которым обеспечивается стабильное кроветворение [1]. В результате деления СК могут образовывать два типа клеток: дочерние клетки, являющиеся идентичными родительской клетке, и клетки, которые уходят в созревающую фракцию и начинают путь дифференцировки. Острый лейкоз представляет собой клеточный клон, все элементы которого являются потомками одной клетки [2]. Первоначальная мутация происходит в стволовой клетке. Генетическая нестабильность приводит к дополнительным мутациям, в результате которых клетки образовавшегося клона перестают дифференцироваться, постепенно поражают костный мозг морфологически незрелыми кроветворными клетками с вытеснением ими нормальных клеток.
На поведение СК влияет их микроокружение или их ниша. Ниши представляют собой пространство для СК, в котором контролируется поведение СК и регулируется их численность через сигналы от клеток и неклеточных факторов. СК в зависимости от сигналов могут или пролиферировать, или находиться в состоянии покоя, или дифференцироваться [3]. Дифференцировка и пролиферация кроветворных клеток происходят параллельно. За счет ниш поддерживается равновесие между различными типами кроветворных клеток.
Лейкозные клетки располагаются в тех же нишах что и гемопоэтические СК и прогениторные клетки, в результате чего имеет место конкуренция за нишу. В частности, лейкозные клетки способны избыточно вырабатывать колониестимулирующий фактор, увеличивающий скорость их деления по сравнению со скоростью деления нормальных клеток (стимулятор миелопоэза), специфически сильнее действующий на лейкозные, чем на нормальные клетки-предшественники гемопоэза [1], [2]. В то же время злокачественные клетки, даже в малом количестве, обладают способностью избирательно угнетать пролиферацию и дифференцировку нормальных предшественников с помощью гуморальных ингибиторов
В результате в нише происходит конкуренция за функциональное пространство между различными клетками [3]. Конкурентное преимущество имеют клетки, которые быстрее пролиферируют, давая многочисленное потомство. Скорость пролиферации СК регулируется сигналами, поступающими от клеток микроокружения. Нарушение функционального состояния ниши приводит к увеличению скорости генерации клеток или к ее уменьшению.
Математическая модель лейкоза
Предлагаемые в литературных источниках математические модели [4], [5], представлены системами обыкновенных дифференциальных уравнений. В работах [6], [7] предлагается модель иммунного отклика на появление лейкозных клеток, а в [8] предлагаются варианты моделирования лечения лейкозов. Уровень заболеваний населения РФ заболеваниям крови отражен в [9]. За основу моделирования лейкоза взята концепция конкуренции всех типов клеток за функциональное пространство [10].
В математической модели предполагается, что лейкоз имеет иерархическую структуру. Рассматривается четыре типа клеток: здоровые, лейкозные, стволовые и клетки микроокружения, регулирующие пролиферацию стволовых клеток. Лейкозные, здоровые и стволовые клетки объединены в один пул единичного объема. Если принять, что ![]() ‑ количество стволовых клеток, находящихся в нише,
‑ количество стволовых клеток, находящихся в нише, ![]() ‑ здоровых,
‑ здоровых, ![]() ‑ лейкозных, то их количество на момент начала кроветворения должно удовлетворять условию
‑ лейкозных, то их количество на момент начала кроветворения должно удовлетворять условию ![]() . Распределение размножающихся стволовых клеток между больными и здоровыми происходит под влиянием клеток микроокружения
. Распределение размножающихся стволовых клеток между больными и здоровыми происходит под влиянием клеток микроокружения ![]() в пропорциях :
в пропорциях : ![]() . Здоровые, больные и стволовые клетки могут самостоятельно размножаться с удельными скоростями равными
. Здоровые, больные и стволовые клетки могут самостоятельно размножаться с удельными скоростями равными ![]() соответственно. Скорости перехода здоровых и больных клеток в кровеносное русло равны
соответственно. Скорости перехода здоровых и больных клеток в кровеносное русло равны ![]() и
и ![]() соответственно. Скорость перехода клеток
соответственно. Скорость перехода клеток ![]() в здоровые и больные регулируется клетками микроокружения
в здоровые и больные регулируется клетками микроокружения ![]() . С учетом этих предположений математическая модель лейкоза представлена задачей Коши для системы четырех обыкновенных дифференциальных уравнений
. С учетом этих предположений математическая модель лейкоза представлена задачей Коши для системы четырех обыкновенных дифференциальных уравнений
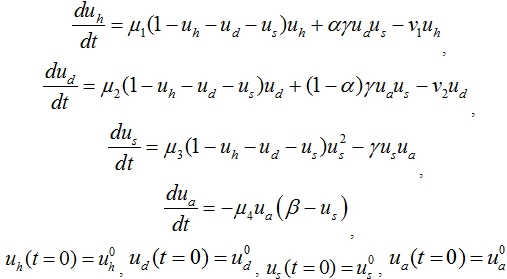 (1)
(1)
Множитель ![]() в первых трех уравнениях представляет собой свободную от клеток часть пула, а параметр
в первых трех уравнениях представляет собой свободную от клеток часть пула, а параметр ![]() соответствует количеству стволовых клеток, находящихся в нише, в равновесном состоянии при естественной генерации всех типов клеток.
соответствует количеству стволовых клеток, находящихся в нише, в равновесном состоянии при естественной генерации всех типов клеток.
Все искомые величины в модели считаются безразмерными. Время t также считается безразмерным, однако, применительно к реальным процессам единица безразмерного времени может быть сопоставлена с сутками в реальном процессе.
Стволовые клетки ![]() под влиянием клеток микроокружения
под влиянием клеток микроокружения ![]() покидают нишу со скоростью
покидают нишу со скоростью ![]() и переходят в профилирующие здоровые
и переходят в профилирующие здоровые ![]() и лейкозные
и лейкозные ![]() клетки. При увеличении количества стволовых клеток в нише выше порогового значения
клетки. При увеличении количества стволовых клеток в нише выше порогового значения ![]() увеличивается и количество клеток микроокружения, вызывающих увеличение скорости ухода стволовых клеток из ниши со скоростью
увеличивается и количество клеток микроокружения, вызывающих увеличение скорости ухода стволовых клеток из ниши со скоростью![]() , а при уменьшении количества стволовых клеток в нише скорость ухода будет уменьшаться.
, а при уменьшении количества стволовых клеток в нише скорость ухода будет уменьшаться.
В случае отсутствия ниши (в (1) ![]() ) первые два уравнения в (1) принимают вид
) первые два уравнения в (1) принимают вид
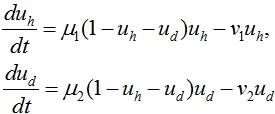 (2)
(2)
Эта система уравнений имеет две стационарные точки
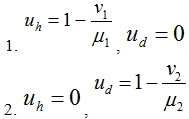
В первой стационарной точке собственными значениями матрицы Якоби правой части уравнений (2) будут
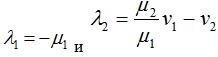
И эта стационарная точка будет устойчивой, если выполняется неравенство ![]() . То есть, если удельная скорость генерации опухолевых клеток мала или скорость их ухода в систему велика, то клетки
. То есть, если удельная скорость генерации опухолевых клеток мала или скорость их ухода в систему велика, то клетки ![]() со временем вытеснят клетки
со временем вытеснят клетки ![]() . Если это неравенство не выполняется, то устойчивой будет вторая стационарная точка.
. Если это неравенство не выполняется, то устойчивой будет вторая стационарная точка.
Модель пересадки клеток
Одним из способов лечения является пересадка донорских клеток. Если их активность выше, чем активность клеток хозяина, то они постепенно вытеснят клетки хозяина. Как показывает практика клинических исследований, донорские клетки не всегда приживаются в новом организме. С учетом этого модель вытеснения клеток хозяина донорскими клетками ![]() будет представлена системой дифференциальных уравнений
будет представлена системой дифференциальных уравнений
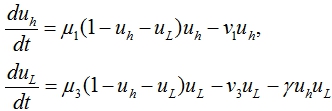 (3)
(3)
в которой ![]() ‑ удельная скорость размножения донорских клеток,
‑ удельная скорость размножения донорских клеток, ![]() ‑ скорость перехода донорских клеток в кровеносное русло. Ингибирующее влияние клеток хозяина на клетки донора учитывается введением во второе уравнение слагаемого
‑ скорость перехода донорских клеток в кровеносное русло. Ингибирующее влияние клеток хозяина на клетки донора учитывается введением во второе уравнение слагаемого ![]() с параметром
с параметром ![]() , определяющим интенсивность ингибирования.
, определяющим интенсивность ингибирования.
Система уравнений (3) имеет три нетривиальные стационарные точки
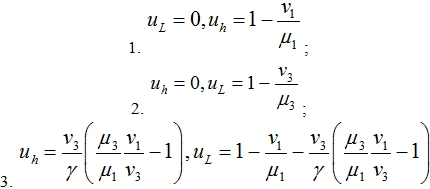
Третья стационарная точки существует, если выполняются неравенства
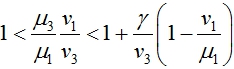
В первой стационарной точке одно из собственных значений матрицы Якоби правой части уравнений (3) будет положительным, если выполняется неравенство
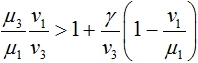
Это неравенство для модели (3) является условием вытеснения донорскими клетками клеток хозяина.
Вторая стационарна точка будет устойчивой, если выполняется неравенство ![]() .
.
В третьей стационарной точке характеристический полином матрицы Якоби правой части уравнений (3)
![]()
имеет корни противоположных знаков. Поэтому эта стационарная точка будет неустойчивой.
Таким образом, в модели (3) донорские клетки либо вытесняют клетки хозяина, либо их вытесняют клетки хозяина.
Модель (3) для случая наличия здоровых и лейкозных клеток принимает вид
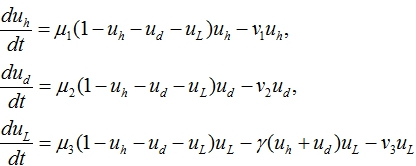
Решение этих уравнений для случая ![]() приведено на рис. 1. Пунктирной линией отмечен момент времени (t=60) пересадки донорских клеток. В этом примере донорские клетки вытесняют и здоровые и лейкозные клетки.
приведено на рис. 1. Пунктирной линией отмечен момент времени (t=60) пересадки донорских клеток. В этом примере донорские клетки вытесняют и здоровые и лейкозные клетки.
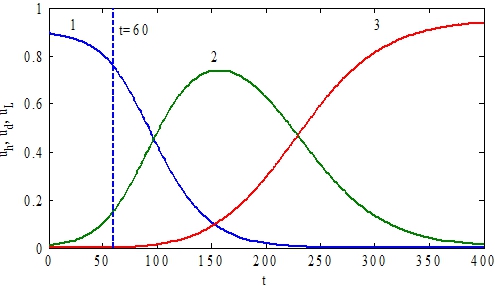
Рис. 1 – Графики зависимости функций ![]() (кривая 1),
(кривая 1), ![]() (кривая 2),
(кривая 2), ![]() (кривая 3) от t при условии, что
(кривая 3) от t при условии, что ![]() при t<60 для случая
при t<60 для случая ![]()
Стационарные точки
Стационарные значения системы уравнений (1) и их устойчивость исследуются с применением численных методов. Для случая констант ![]() на рис. 2 приведена зависимость стационарных значений
на рис. 2 приведена зависимость стационарных значений ![]() от значений параметра
от значений параметра ![]() . Кривая 1 соответствует значениям
. Кривая 1 соответствует значениям ![]() кривая 2 ‑
кривая 2 ‑ ![]() . Пунктирная линия отображает границу между областью устойчивых (
. Пунктирная линия отображает границу между областью устойчивых (![]() ) и областью неустойчивых (
) и областью неустойчивых (![]() ) стационарных точек. В области устойчивых стационарных точек кривые 1 и 2, практически, совпадают.
) стационарных точек. В области устойчивых стационарных точек кривые 1 и 2, практически, совпадают.
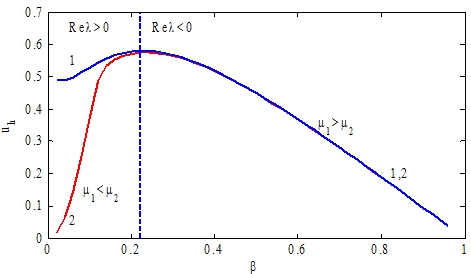
Рис. 2 – Графики зависимости стационарных значений ![]() от параметра
от параметра ![]() . Кривая 1 ‑
. Кривая 1 ‑ ![]() кривая 2 ‑
кривая 2 ‑ ![]() . Пунктирная линия отображает границу раздела между областями устойчивых (
. Пунктирная линия отображает границу раздела между областями устойчивых (![]() ) и неустойчивых (
) и неустойчивых (![]() ) стационарных точек
) стационарных точек
Стационарные точки системы уравнений (1) в зависимости от значений параметра ![]() могут быть как устойчивыми, так и неустойчивыми. При малых значениях параметра
могут быть как устойчивыми, так и неустойчивыми. При малых значениях параметра ![]() в системе возникают колебания. Последнее интерпретируется как возникновение заболевания при недостатке стволовых клеток. На рис. 3 при значениях параметров
в системе возникают колебания. Последнее интерпретируется как возникновение заболевания при недостатке стволовых клеток. На рис. 3 при значениях параметров ![]() отражено изменение
отражено изменение ![]() ,
, ![]() и
и ![]() во времени. Стационарная точка в рассматриваемом случае не является устойчивой – в ее окрестности возникают периодические колебания.
во времени. Стационарная точка в рассматриваемом случае не является устойчивой – в ее окрестности возникают периодические колебания.
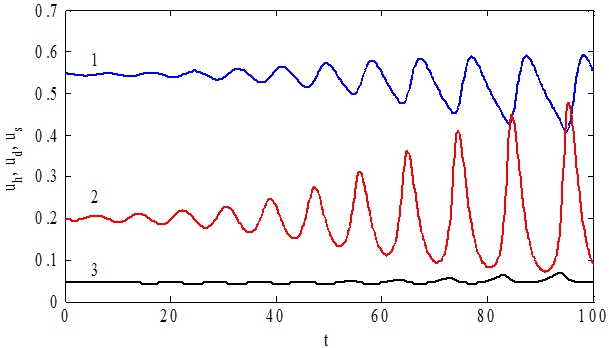
Рис. 3 – Графики зависимости функций ![]() (кривая 1),
(кривая 1), ![]() (кивая 2),
(кивая 2), ![]() от t при малых начальных отклонениях от неустойчивой стационарной точки
от t при малых начальных отклонениях от неустойчивой стационарной точки
Модель лечения заболевания
Возникновение заболевания в модели (1) рассматривается как изменение в момент времени ![]() параметра
параметра ![]() , переводящее устойчивое стационарное состояние в неустойчивое. Тогда под лечением понимается такое воздействие на этот параметр, при котором он возвращается в «нормальное» состояние. При этом введение препарата происходит от момента времени
, переводящее устойчивое стационарное состояние в неустойчивое. Тогда под лечением понимается такое воздействие на этот параметр, при котором он возвращается в «нормальное» состояние. При этом введение препарата происходит от момента времени ![]() до
до ![]() момента времени . Пусть
момента времени . Пусть ![]() ‑ отклонение параметра
‑ отклонение параметра ![]() от исходного значения, а
от исходного значения, а ![]() ‑ закон введения препаратов, изменяющих значение возмущения
‑ закон введения препаратов, изменяющих значение возмущения ![]() . Тогда модель нарушения функционирования генерации клеток и лечения нарушений с учетом четвертого уравнения в (1) принимает вид
. Тогда модель нарушения функционирования генерации клеток и лечения нарушений с учетом четвертого уравнения в (1) принимает вид
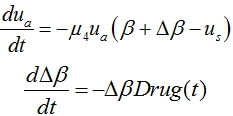
Препараты могут подаваться непрерывно во времени (![]() ) или периодически. Модель периодического воздействия может быть представлена функцией
) или периодически. Модель периодического воздействия может быть представлена функцией
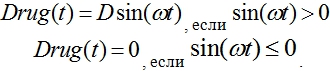
Результаты моделирования для этой функции представлены на рис. 4 в виде зависимостей![]() ,
, ![]() и
и ![]() .
.
Для случая констант ![]() стационарная точка
стационарная точка ![]() является устойчивой на временном промежутке
является устойчивой на временном промежутке ![]() (на рис. 4 зона ). В момент времени
(на рис. 4 зона ). В момент времени ![]() параметр
параметр ![]() принимает значение 0.20. Стационарная точка системы уравнений (1) при этом значении параметра
принимает значение 0.20. Стационарная точка системы уравнений (1) при этом значении параметра ![]() будет неустойчивой (рис. 2). В системе возникают колебания (на рис. 4 зона B). То есть система переходит в неустойчивое состояние. С момента времени
будет неустойчивой (рис. 2). В системе возникают колебания (на рис. 4 зона B). То есть система переходит в неустойчивое состояние. С момента времени ![]() до момента времени
до момента времени ![]() вводится препарат с
вводится препарат с ![]() (зона Drug на рис. 4). Постепенное уменьшение возмущения параметра
(зона Drug на рис. 4). Постепенное уменьшение возмущения параметра ![]() переводит систему в область устойчивых стационарных точек.
переводит систему в область устойчивых стационарных точек.
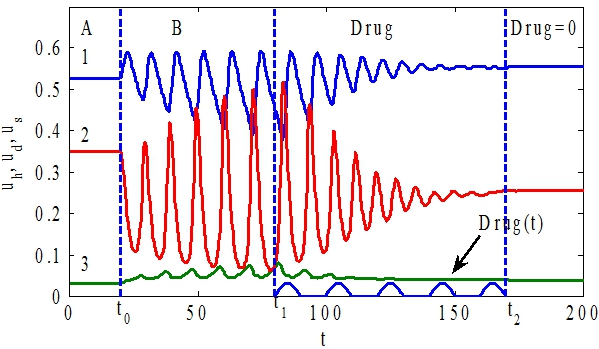
Рис. 4 ‑ Графики зависимости функций ![]() (кривая 1),
(кривая 1), ![]() (кивая 2),
(кивая 2), ![]() (кривая 3) и
(кривая 3) и ![]() от t. На промежутке
от t. На промежутке ![]() система находится в равновесном состоянии (зона А), на промежутке
система находится в равновесном состоянии (зона А), на промежутке ![]() в неустойчивом состоянии (зона В), на промежутке
в неустойчивом состоянии (зона В), на промежутке![]() (зона Drug ) происходит возврат системы в устойчивое состояние
(зона Drug ) происходит возврат системы в устойчивое состояние
Решение задачи Коши для систем дифференциальных уравнений осуществлялось с применением метода Рунге-Кутты в модификации Дорманда-Принса в среде программирования математического пакета MatLab. Использовалась встроенная функция ode45. Параметры систем уравнений ![]() определяющие скорости реакций, как следует из результатов клинических исследований, могут отличаться в 2-3 раза. В этом диапазоне отличия параметров системы уравнений не являются жесткими. Тем не менее, поскольку решения строились в окрестности неустойчивых точек, результаты решения сопоставлялись с решениями, построенными с использованием функции ode23tb, предназначенной для решения «жестких» систем. Результаты, поостренными обеими функциями с точностью 10-6 совпали в исследуемом диапазоне изменения параметров.
определяющие скорости реакций, как следует из результатов клинических исследований, могут отличаться в 2-3 раза. В этом диапазоне отличия параметров системы уравнений не являются жесткими. Тем не менее, поскольку решения строились в окрестности неустойчивых точек, результаты решения сопоставлялись с решениями, построенными с использованием функции ode23tb, предназначенной для решения «жестких» систем. Результаты, поостренными обеими функциями с точностью 10-6 совпали в исследуемом диапазоне изменения параметров.
Заключение
Таким образом, разработанная модель объясняет механизм взаимодействия нескольких типов клеток как конкуренцию за функциональное пространство с вытеснением из него всех клеток более активными клетками, а нарушение функций кроветворения как переход системы из устойчивой области в неустойчивую.
Список литературы / References
- Савостьянов Г.А. Возникновение стволовых клеток в развитии многоклеточности и их количественная характеристика / Г. А. Савостьянов // Цитология. – 2016. – Т. 58. – № 8. – С. 577–593.
- Копнин Б.П. Современные представления о механизмах злокачественного роста: сходства и различия солидных опухолей и лейкозов / Б.П. Копнин // Клиническая онкогематология. – 2012. – №5(3). – С. 165–185.
- Васильев А.В. Ниши стволовых клеток и регенеративная медицина / А. В. Васильев, Е. А. Воротеляк, В. В. Терских // Российский физиологический журнал им. И.М. Сеченова. – 2016. – №103(3). – С. 241–261.
- Fuentes-Garí M. A mathematical model of subpopulation kinetics for the deconvolution of leukaemia heterogeneity / M. Fuentes-Garí, R. Misener, D. García-Munzer and others // Journal of the Royal Society Interface. – 2015. – V. 12. – № 108. 20150276. doi:10.1098/rsif.2015.0276.
- Berezansky L. Stability and Controllability Issues in Mathematical Modeling of the Intensive Treatment of Leukemia / L. Berezansky, S. Bunimovich-Mendrazitsky, B. Shklyar // Journal of Optimization Theory and Applications. – 2015. – V. 167. – № 1. – P. 326–341. doi:1007/s10957-015-0717-9.
- Rǎdulescu I. R. A complex mathematical model with competition in Leukemia with immune response - An optimal control approach / I. R. Rǎdulescu, D. Cândea, A. Halanay // IFIP Advances in Information and Communication Technology. – 2016. – V. 494. – P. 430–441.doi:1063/1.4765573
- Bunimovich-Mendrazitsky C. Mathematical model of pulsed immunotherapy for bladder cancer / C. Bunimovich-Mendrazitsky, H. Byrne , L. Stone // Bulletin of mathematical biology. – 2008. –V.70. –№ 7. – P. 2055–2076. doi:10.1007/s11538-008-9344-z.
- Clapp G. A review of mathematical models for leukemia and lymphoma / G. Clapp, D. Levy // Drug Discovery Today: Disease Models. – 2015, V. 16. – № 2. – P. 1–6.
- Kolpak E. P. Neoplasm Morbidity among the Population of Russia / E. P. Kolpak, I. S. Frantsuzova, K. V. Kuvshinova // International journal of advanced biotechnology and research. – 2017. – V.8. – № 3 – P. 2315–2322.
- Жукова И.В. Математические модели злокачественной опухоли / И. В. Жукова, E. П. Колпак // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. – 2014. – № – С. 5–18.
Список литературы на английском языке / References in English
- Savostyanov G. A. Vozniknovenie stvolovyh kletok v razvitii mnogokletochnosti i ih kolichestvennaja harakteristika [The initiation of stem cells in the development of multicellularity and their quantitative characteristics] / G. A. Savostyanov // Citologiya [Cytology]. – 2016. – Vol. 58. – №8. –P. 577–593. [in Russian]
- Kopnin B. P. Sovremennye predstavlenija o mehanizmah zlokachestvennogo rosta: shodstva i razlichija solidnyh opuholej i lejkozov [Modern views on the mechanisms of malignant growth: the similarities and differences of solid tumors and leukemias] / B. P. Kopnin // Klinicheskaya onkogematologiya [Clinical oncohematology]. – 2012. –№ 5(3). – P. 165–185. [in Russian]
- Vasil'ev A. V. Nishi stvolovyh kletok i regenerativnaja medicina [Niches of stem cells and regenerative medicine] / A. V. Vasil’ev, E. A. Vorotelyak, V. V. Terskikh // Rossijskij fiziologicheskij zhurnal im. I. M. Sechenova [Russian physiological journal named after I. M. Sechenov]. –2016. –№103(3). – P. 241–261. [in Russian]
- Fuentes-Garí M. A mathematical model of subpopulation kinetics for the deconvolution of leukaemia heterogeneity / M. Fuentes-Garí, R. Misener, D. García-Munzer and others // Journal of the Royal Society Interface. – 2015. – V. 12. – № 108. 20150276. doi:10.1098/rsif.2015.0276.
- Berezansky L. Stability and Controllability Issues in Mathematical Modeling of the Intensive Treatment of Leukemia / L. Berezansky, S. Bunimovich-Mendrazitsky, B. Shklyar // Journal of Optimization Theory and Applications. – 2015. – V. 167. – № 1. – P. 326–341. doi:1007/s10957-015-0717-9.
- Rǎdulescu I. R. A complex mathematical model with competition in Leukemia with immune response - An optimal control approach / I. R. Rǎdulescu, D. Cândea, A. Halanay // IFIP Advances in Information and Communication Technology. – 2016. – V. 494. – P. 430–441.doi:1063/1.47655733.
- Bunimovich-Mendrazitsky C. Mathematical model of pulsed immunotherapy for bladder cancer / C. Bunimovich-Mendrazitsky, H. Byrne , L. Stone // Bulletin of mathematical biology. – 2008. –V.70. –№ 7. – P. 2055–2076. doi:10.1007/s11538-008-9344-z.
- Clapp G. A review of mathematical models for leukemia and lymphoma / G. Clapp, D. Levy // Drug Discovery Today: Disease Models. ‑ 2015, V. 16. – № 2. – P. 1–6.
- Kolpak E. P. Neoplasm Morbidity among the Population of Russia / E. P. Kolpak, I. S. Frantsuzova, K. V. Kuvshinova // International journal of advanced biotechnology and research. – 2017. – V.8. – № 3 – P. 2315–2322.
- Zhukova I. V. Matematicheskie modeli zlokachestvennoj opuholi [Mathematical models of malignant tumor] / I. V. Zhukova, E. P. Kolpak // Vestnik Sankt-Peterburgskogo universiteta. Serija 10: Prikladnaya matematika. Informatika. Processy upravlenija [Bulletin of Saint-Petersburg university. Series 10: Applied mathematics. Informatics. Control processes]. –2014. –№3. – P. 5–18. [in Russian]
