Monte Carlo simulation of high-energy particle transport in hybrid perovskites doped with europium
Monte Carlo simulation of high-energy particle transport in hybrid perovskites doped with europium
Abstract
The work studies the interaction of accelerated electrons, protons, and neutrons with the double-cation hybrid perovskite CsFAPbI3, containing partial substitution of lead with Eu. Using the GEANT4 package, particle transport and energy release distribution were simulated in 1 cm thick samples. It is shown that electrons with an energy of 10 MeV and protons with an energy of 18 MeV are completely decelerated in the material, forming pronounced areas of absorbed energy, while 5 MeV neutrons show weak interaction with the sample. A change in Eu concentration in the range of 1–10% does not significantly affect the macroscopic characteristics of the processes. The obtained results provide an evaluation of the distribution and magnitude of energy losses.
1. Введение
В последние годы перовскитные соединения оказались в центре внимания оптоэлектронного сообщества благодаря набору характеристик, который редко встречается у других классов полупроводниковых материалов. Они эффективно поглощают свет, позволяют гибко регулировать ширину запрещённой зоны, отличаются высокой фотолюминесцентной отдачей и одновременно остаются технологически простыми и химически адаптивными системами
, . Такой баланс свойств ускорил прогресс в создании перовскитных фотопреобразователей, светодиодов и сенсоров, причём достигнутая эффективность перовскитных солнечных модулей уже превысила 26% . Благодаря малой массе, высокой энергоотдаче и низким производственным затратам эти материалы рассматриваются и как потенциальная основа для энергетики космических аппаратов, где требования к удельным параметрам особенно жёсткие , .Однако эксплуатация перовскитов в космосе сопряжена с рядом факторов, которые могут резко ограничивать их ресурс. Помимо перепадов температуры и жёсткого ультрафиолета, ключевым деструктивным агентом остаются потоки ионизирующих частиц — электронов, протонов, нейтронов и тяжёлых ядер. Их взаимодействие с материалом инициирует образование вакансий и смещения атомов, вызывает локальные электронные возбуждения, а продукты вторичных процессов дополнительно усиливают радиационные повреждения. Это приводит к падению фотоэлектрических характеристик, увеличению токов утечки и возникновению стабильных дефектных областей
, , , . В результате даже при всех технологических преимуществах гибридные галидные перовскиты часто оказываются недостаточно устойчивыми к высокоэнергетическому облучению.В настоящем исследовании с применением метода Монте-Карло и программного комплекса GEANT4
, выполнено моделирование проникновения и энерговыделения ускоренных электронов, протонов и нейтронов в двухкатионном перовските CsFAPbI3, в котором часть ионов свинца замещена европием. Данная модификация ранее демонстрировала повышенную стабильность при воздействии потоков электронов , что делает её перспективным объектом анализа в контексте радиационной стойкости.2. Методы и принципы исследования
Для оценки радиационных эффектов, возникающих при воздействии ускоренных электронов, нейтронов и протонов на двухкатионный гибридный галидный перовскит с частичным замещением B-катиона на Eu, была использована вычислительная среда GEANT4. Расчёты выполнялись для объёмных образцов толщиной 1 см. Реальные перовскитные слои в солнечных элементах имеют толщину порядка 200–500 нм, однако моделирование таких малых толщин требует либо экстремально больших потоков частиц, либо недостижимо длительного расчётного времени. GEANT4 допускает моделирование потоков вплоть до 9,9·109 частиц/см2, но использование такого значения приводит к резкому росту вычислительной нагрузки. Увеличение толщины материала на четыре порядка — от сотен нанометров до сантиметра — позволяет повысить вероятность взаимодействий примерно в 2·106 раз. Поэтому выбор толщины 1 см при потоке 105 частиц/см2 обеспечивает статистическую эквивалентность облучению тонкого (≈0,5 мкм) активного слоя при потоке порядка 1011 частиц/см2.
Состав материала задавался на основе элементных характеристик: атомного номера и массы, массовых долей компонентов, плотности и геометрических размеров образцов.
Для корректного описания взаимодействий использовался расширенный перечень электромагнитных и адронных процессов, рассчитанных на высокоточные задачи в широком диапазоне энергий. Комптоновское рассеяние моделировалось в соответствии с формализмом Клейна–Нишины, переходящим при низких энергиях в томсоновский предел и учитывающим релятивистские поправки на высоких энергиях. Для множественного рассеяния использовалась модель G4UrbanMscModel, обеспечивающая более реалистичное описание отклонений траекторий в плотных средах.
В модуле GammaNuclearPhysics были определены гамма-ядерные реакции и энергетические границы, при превышении которых выбор модели переключался с G4LowGammaNuclearModel (E = 0–Emax1) на G4CascadeInterface (E = Emax₁–Emax₂). В HadronElasticPhysicsHP задавались параметры упругого взаимодействия нейтронов.
PhysicsList включал:
• набор электромагнитных процессов G4EmStandardPhysicsWVI, предназначенный для высокоточного описания прохождения заряженных частиц и фотонов; модель G4WentzelVIModel применялась для множественного и одиночного рассеяния e⁺/e⁻ при любых энергиях; ионная ионизация рассчитывалась по модели Линдхарда–Соренсена;
• ограничение минимального шага генерации вторичных частиц;
• процессы переноса и распада частиц (G4Decay и G4RadioactiveDecayBase);
• включённый расчёт CSDARange, позволяющий определять средний пробег заряженной частицы без учёта рассеяния;
• адронные процессы: упругое и неупругое взаимодействие (G4HadronElasticPhysicsHP, G4HadronInelasticQBBC), аналогичные процессы для ионов (G4IonElasticPhysics и G4IonPhysicsXS), высокоточное описание нейтронов (G4NeutronCrossSectionXS, G4HadronPhysicsShieldingLEND), остановка адронов (G4StoppingPhysics), гамма-ядерные реакции (GammaNuclearPhysics).
Дополнительно подключались процессы переноса и распада частиц (G4Decay, G4RadioactiveDecayBase).
В классе SteppingAction рассчитывались полная поглощённая энергия и неионизационные потери с использованием функций GetTotalEnergyDeposit и GetNonIonizingEnergyDeposit. При необходимости для NIEL можно применять fNIELCalculator с данными по тормозным способностям различных материалов или класс G4ScreenedNuclearRecoil с функцией NIELPartitionFunction (модель Линхарда–Робинсона), что важно для высокоэнергетических частиц — протонов, α-частиц, тяжёлых ионов.
Используемые энергии электронов (10 МэВ) и протонов (18 МэВ) соответствовали доступным экспериментальным параметрам. Нейтронная энергия 5 МэВ выбрана как характерная для Pu-Be источников и попадает в наиболее вероятный для околоземных орбит диапазон 0,1–15 МэВ
, .На рис. 1 и 2 приведены распределения энергии и глубины проникновения 10-МэВ электронов в CsFAPbI₃ с содержанием Eu 1–10%. Варьирование доли европия практически не отражается на характеристиках пробега частиц. Длина трека большинства электронов превышает 10 см — они способны пройти материал насквозь, многократно рассеиваясь и увеличивая общий путь. Тем не менее распределение по глубине (рис. 2a) показывает, что значительная часть электронов полностью теряет энергию и не покидает пределы образца. Длина свободного хода может достигать сотен микрон (рис. 1b), количество актов рассеяния обычно составляет 30–100 (рис. 1с). Частицы, проходящие через образец, теряют не менее 4 МэВ (рис. 1e), при этом неионизационные потери остаются ниже ~1 кэВ (рис. 1d). Максимум энерговыделения приходится на глубину 2–5 см (рис. 2b,c). Энергии вторичных частиц — как нейтральных (преимущественно γ-квантов), так и заряженных — не превышают нескольких сотен кэВ (рис. 1f,g).
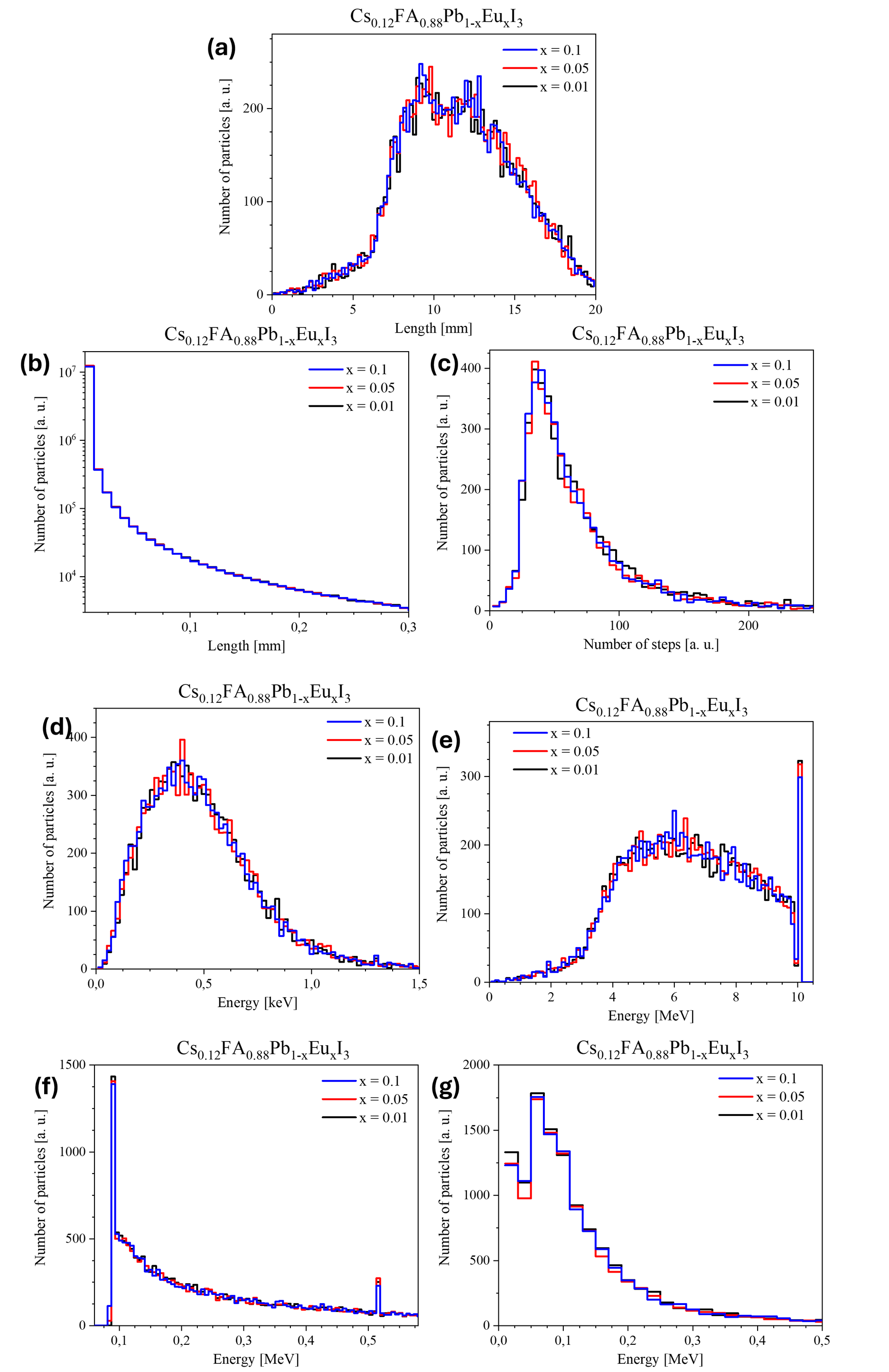
Рисунок 1 - Результаты воздействия электронов с энергией 10 МэВ на гибридный перовскит Cs0,12FA0,88Pb1-xEuxI3 (x = 0,01, 0,05, 0,1):
а – длина треков электронов; b – длина шага моделирования; с – число шагов моделирования; d – неионизационные потери; e – общие потери энергии электронами; f – энергия вторичных нейтральных частиц; g – энергия вторичных заряженных частиц
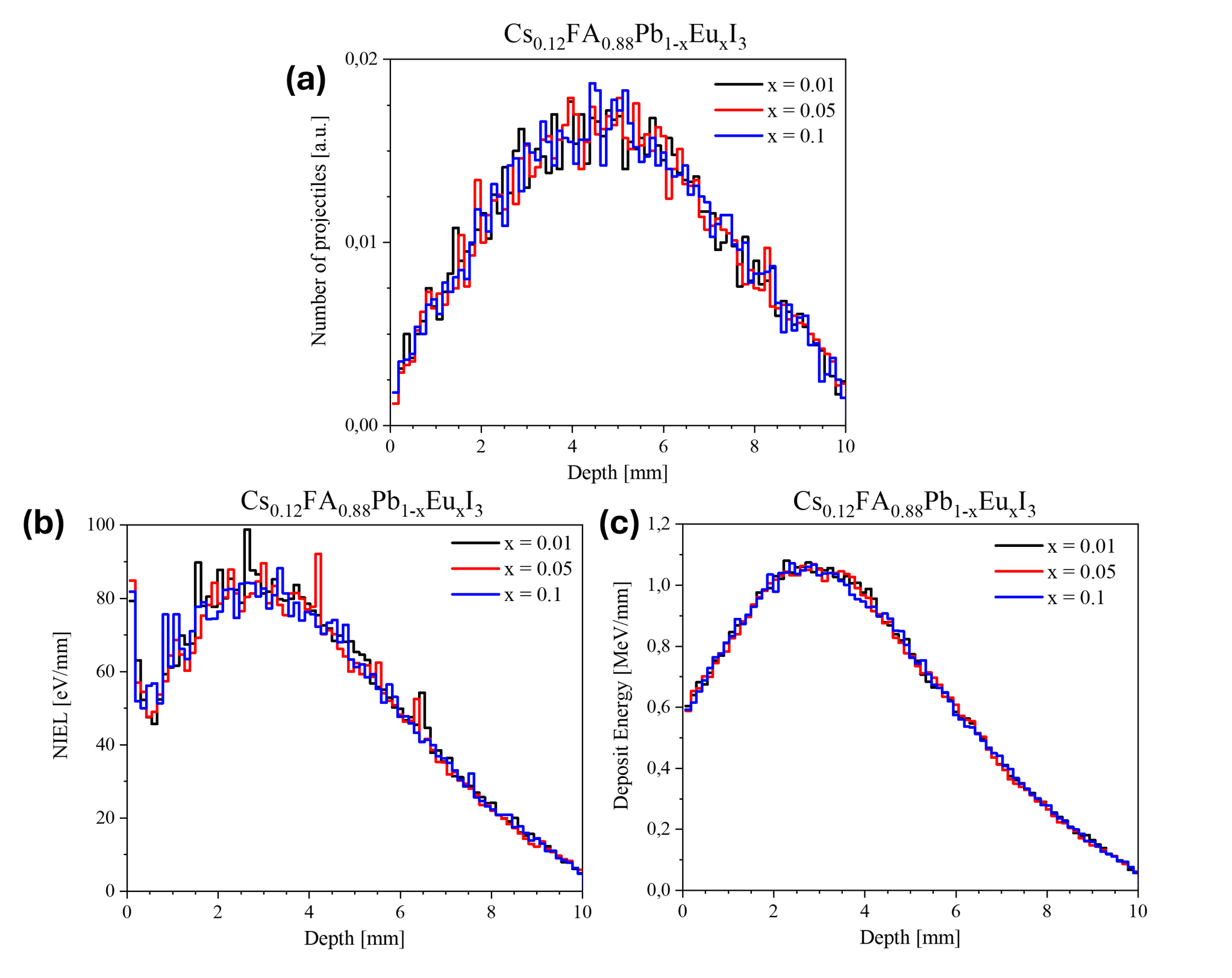
Рисунок 2 - Результаты воздействия электронов с энергией 10 МэВ на гибридный перовскит Cs0,12FA0,88Pb1-xEuxI3 (x = 0,01, 0,05, 0,1):
а – глубина пробега электронов; b – распределение неионизационных потерь энергии электронами по глубине; с – распределение потерь энергии электронами по глубине
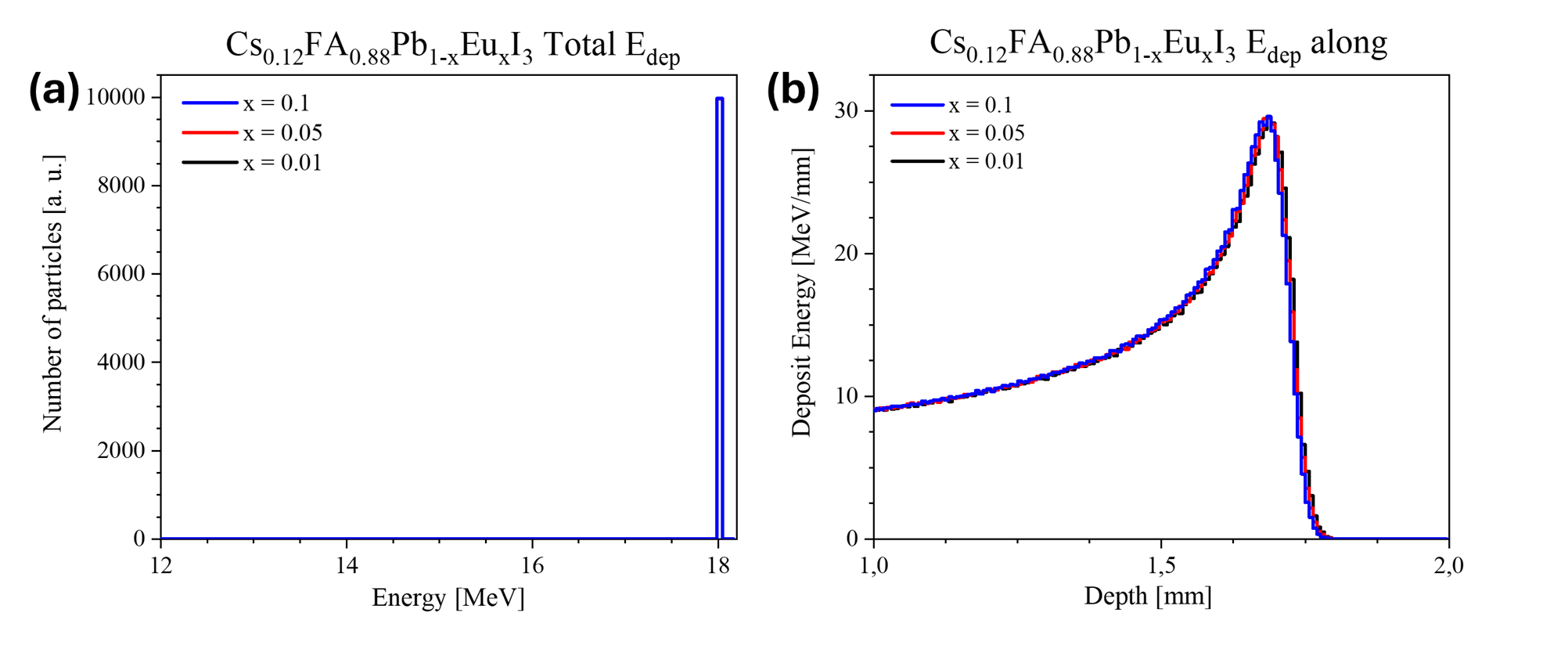
Рисунок 3 - Результаты воздействия протонов с энергией 18 МэВ на гибридный перовскит Cs0,12FA0,88Pb1-xEuxI3 (x = 0,01, 0,05, 0,1):
а – общие потери энергии протонами; b – распределение потерь энергии протонами по глубине
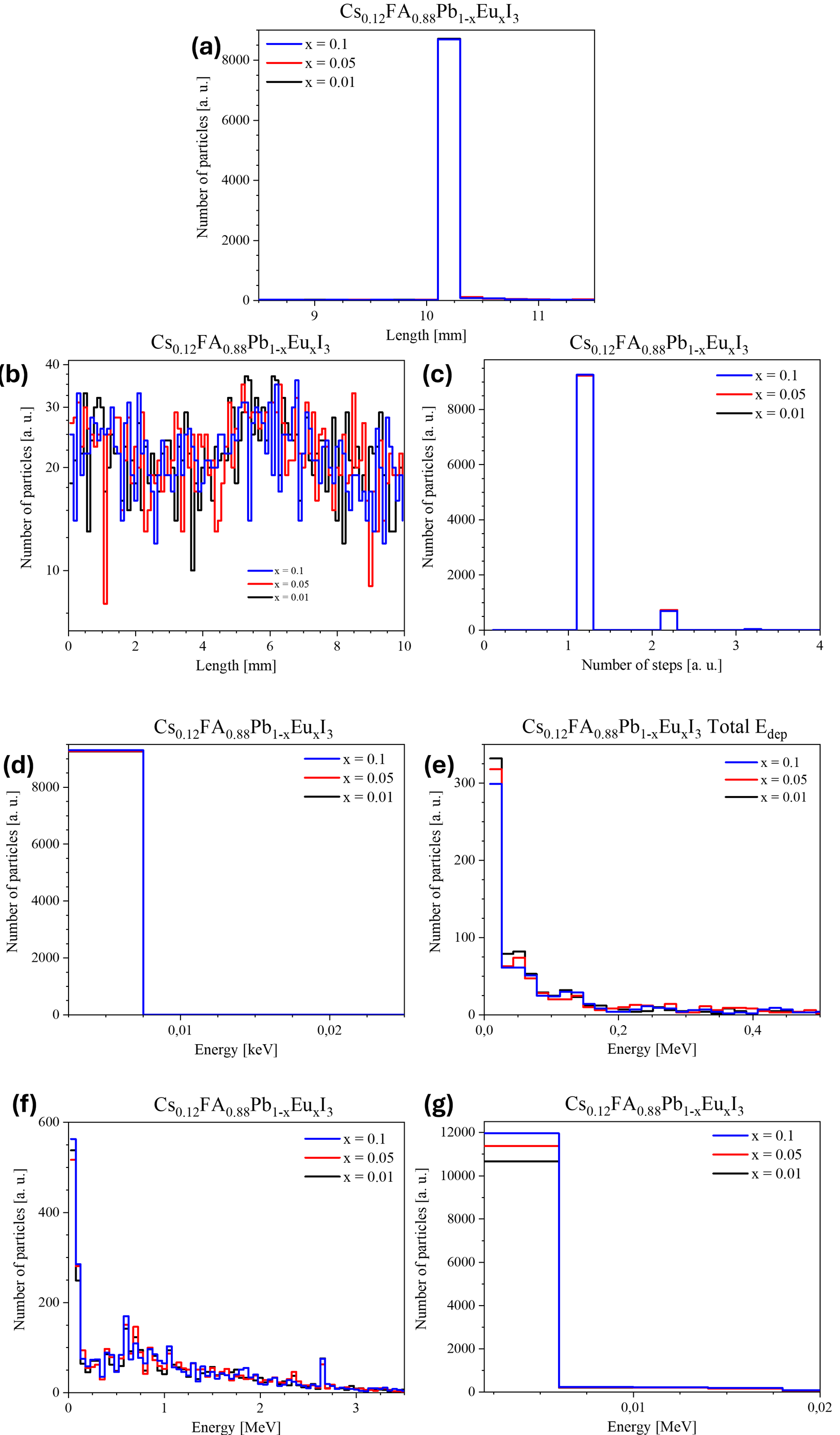
Рисунок 4 - Результаты воздействия нейтронов с энергией 5 МэВ на гибридный перовскит Cs0,12FA0,88Pb1-xEuxI3 (x = 0,01, 0,05, 0,1):
а – длина треков нейтронов; b – длина шага моделирования; с – число шагов моделирования; d – неионизационные потери; e – общие потери энергии нейтронами; f – энергия вторичных нейтральных частиц; g – энергия вторичных заряженных частиц
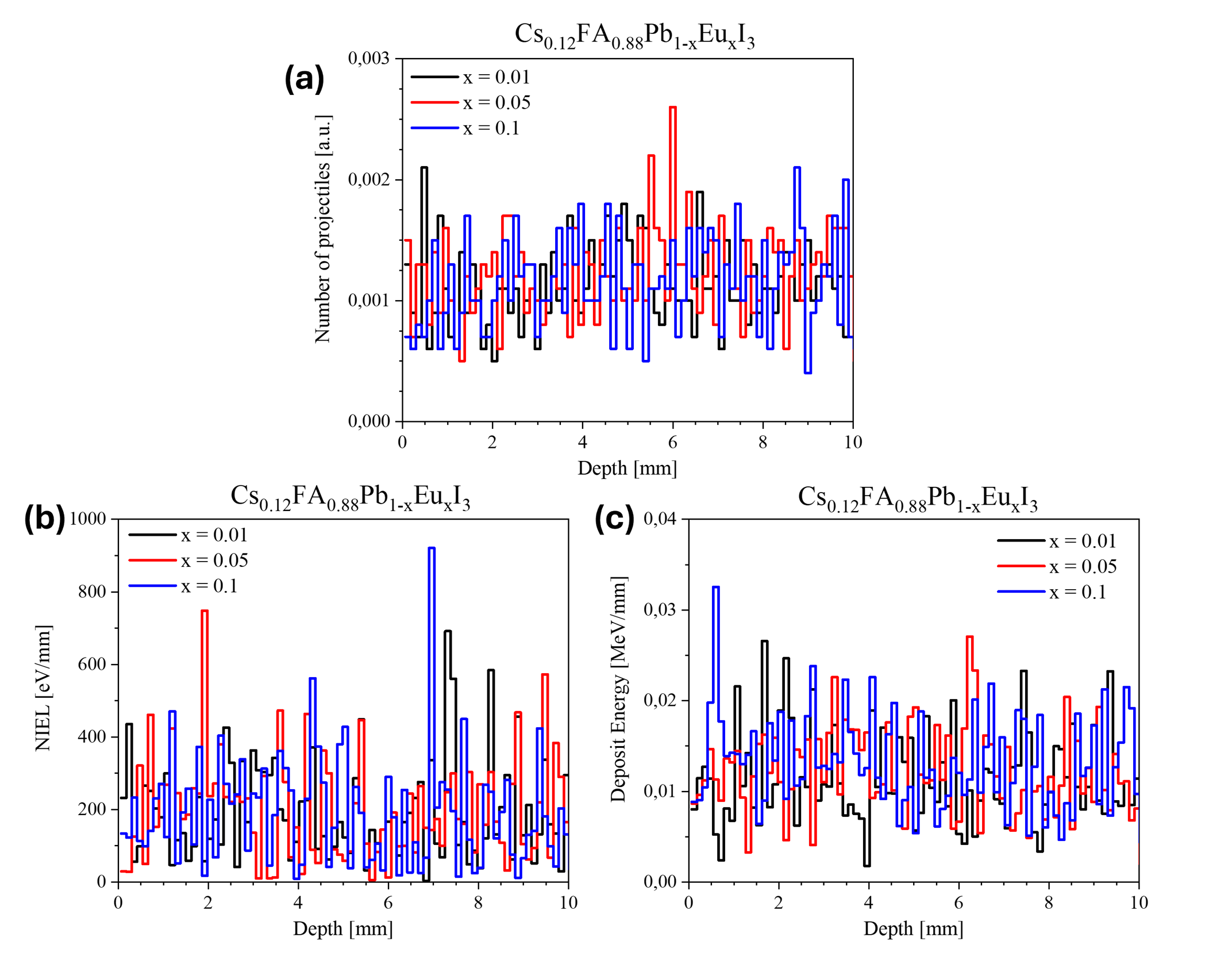
Рисунок 5 - Результаты воздействия нейтронов с энергией 5 МэВ на гибридный перовскит Cs0,12FA0,88Pb1-xEuxI3 (x = 0,01, 0,05, 0,1):
а – глубина пробега нейтронов; b – распределение неионизационных потерь энергии нейтронами по глубине; с – распределение потерь энергии нейтронами по глубине
3. Заключение
Проведённое моделирование позволило количественно оценить характер энергетических потерь электронов, протонов и нейтронов в двухкатионном перовските CsFAPbI3 с частичным замещением свинца на Eu. Результаты показывают, что при энергиях электроны 10 МэВ и протонов 18 МэВ полностью теряют энергию в материале, формируя выраженные области энерговыделения в глубине образца, тогда как нейтроны с энергией 5 МэВ практически не взаимодействуют с веществом. Изменение концентрации Eu в изученном диапазоне не оказывает заметного влияния на макроскопические параметры взаимодействия частиц.
Однако расчёты в GEANT4 описывают только транспорт частиц, энерговыделение и виды радиационных эффектов взаимодействия излучения с веществом и не позволяют напрямую определить образование точечных дефектов, динамику решётки и эволюцию повреждений. Поэтому полученные данные необходимо рассматривать как первый уровень анализа радиационной стойкости. Для оценки микроскопических последствий облучения требуется дополнить работу методами атомистического моделирования — расчётами DFT для определения энергий дефектообразования и миграции, а также молекулярно-динамическими симуляциями каскадов смещений.
