EVALUATING THE INFLUENCE OF TEMPERATURE AND MULTIPARTICLE INTERACTION ON THE DOMAIN STRUCTURE OF SMALL MAGNETIC SYSTEMS

Технология синтеза низкоразмерных структур в последние десятилетие вышла на уровень промышленного масштаба. Области применения одномерных и двумерных материалов постепенно расширяются и необходимо понимание их критического поведения.  В мире синтезируются все новые магнетики с пониженной размерностью и это открывает возможности экспериментального измерения энергетических характеристик межспинового взаимодействия для более точного моделирования критического поведения магнитной системы [1], [2]. При определенных внешних параметрах реализуются критические условия, в которых поведением системы можно управлять в широком диапазоне даже незначительными изменениями внешней среды [3].  Но при приближении температуры к критическому значению наблюдается аномальное увеличение времени релаксации флуктуирующих величин и возникают сложности динамического описания этих процессов. Компьютерное моделирование позволяет предсказать поведение таких систем и дает представление о направлении дальнейшего исследования [4]. Для описания магнитных свойств одноцепочечных магнетиков чаще всего используются обобщения модели Изинга и модель Гейзерберга [5], [6].

В нашей работе используется модель Изинга с модификацией для учета взаимодействия дальних магнитных моментов, что позволяет приблизить ее к реальному поведению системы [7]. Был разработан комплекс программ для моделирования доменных структур вблизи критической точки [8], [9].

В одномерную модель Изинга заложена цепочечная структура спинов Si, которые принимают дискретное значение в зависимости от соноправленности с выбранным направлением («+1» если сонаправлен или «-1» если нет). Конфигурация задается последовательностью спиновых значений для всех узлов решетки и ее энергия рассчитывается по гамильтониану:

(1)

Классическая модель модифицирована с учетом экспериментальных данных об обменном взаимодействии в низкоразмерных решетках и учитывает взаимодействие дальнего порядка. Многоспиновый момент реализуемый в кристаллах учитывается через четырехчастичное взаимодействие спинов [10]. Энергия обменных взаимодействий нормируется в единицах J1. Объектом исследования выступает переход из антиферромагнитной фазы в ферромагнитную, граничные условия задаются «оборванными концами». Следует понимать, что в модели узлом решетки может быть атомная плоскость или группа атомов, или молекул. Алгоритм Метрополиса с динамикой опрокидывания спина является вполне разумным приближением к реальной динамике анизотропного магнетика спины, которого связаны с колебаниями решетки. Эта связь приводит к беспорядочному опрокидыванию спинов. Такой стохастический процесс, по сути, соответствует процессу генерируемому методом Монте-Карло в рамках алгоритма.

Задачей нашей работы было проследить температурное влияние на зарождение магнитных фаз и их смену при изменении параметров системы. Температурную трансформацию диаграмм рассмотрим на примере малой магнитной системы из пяти условных точек. Построение проводилось в плоскости значений энергии обменного взаимодействия J2 (вторая координационная сфера) и проекции внешнего магнитного поля Н. На диаграмме соответствующей абсолютному нулю (рис.1, а) магнитные фазы сгруппированы в восемь областей: 2 ферромагнитных области (1 и 2) отличающиеся наибольшей стабильностью и направлением результирующего магнитного момента; структуры 3 и 4 содержат антиферромагнитные области с чередующимися парами спинов (↑↑↓↓); участки 5 и 6, 7 и 8 соответствуют антиферромагнитным конфигурациям с дефектом: «лишний» спин «блуждает» в системе, нарушая антиферромагнитное построение.

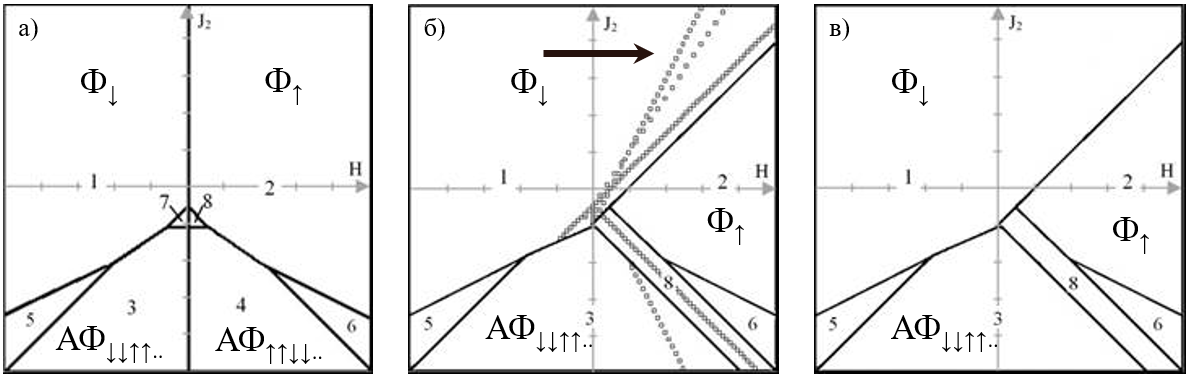
Рисунок 1 - Температурная адаптация диаграмм магнитных состояний:

a – диаграмма, соответствующая абсолютному нулю; б – поглощение второй ферромагнитной фазы первой; в – итоговая диаграмма

DOI:10.23670/IRJ.2022.126.56.1

При построении фазовых диаграмм образец с определенной обменной энергией проходит несколько этапов: переход из антиферромагнитной фазы в ферромагнитную, затем, после установления равновесия происходит увеличение напряженности внешнего магнитного поля с заданным шагом. Система после каждого изменения внешнего параметра приходит в равновесие. Это позволяет в каждой точке диаграммы отображать результат процесса перехода системы в состояние с новым значением напряженности поля. При этом за начальную конфигурацию берется конфигурация из предыдущей точки диаграммы для данного J2. Направление процесса указано стрелкой на рисунке 1, б.

При температуре Т=0,01 (здесь и далее выражена в единицах J1/kБ) по сравнению с диаграммами основных состояний происходит поглощение второй ферромагнитной фазы первой (рис. 1, б). Данный феномен можно трактовать как запаздывание в перестройке магнитной структуры при увеличении внешнего магнитного поля, ведь начальными при Н=0 являются конфигурации, когда все спины направлены вниз, что будет метастабильным состоянием при положительной напряженности внешнего магнитного поля. Для выхода из этого состояния значительного процента конфигураций необходимо либо увеличение температуры системы, либо сильное магнитное поле. В результате при низких температурах наблюдается значительное запаздывание при переходе из ферромагнитной фазы с результирующим магнитным моментом направленным вниз в фазу со спинами направленным вверх. Данные эффект наблюдается и в системах с большим количеством узлов, что говорит о его универсальности. Магнитное упорядочение участка 3 при данной температуре полностью поглощает область 4, которая в данных условиях теряет устойчивость. При этом температура не оказывает влияние на участки 5 и 6. Фаза 7 не реализуется, а фаза 8 становится более стабильной и проявляется для большего диапазона отрицательных значения энергии взаимодействия J2. На диаграмме появляются точки с конфигурациями имеющий низкий процент реализации (менее 10%) в которых энергия оказывается равной энергии доминирующей фазы. Для удобства визуальной интерпретации принято решение их не изображать на диаграммах. Что позволило нам прийти к виду диаграмм на рис. 1, в.

Проследим изменения, происходящие при увеличении относительной температуры системы. Данная группа диаграмм построена для такого же числа узлов магнетика, что и диаграммы на рисунке 1.

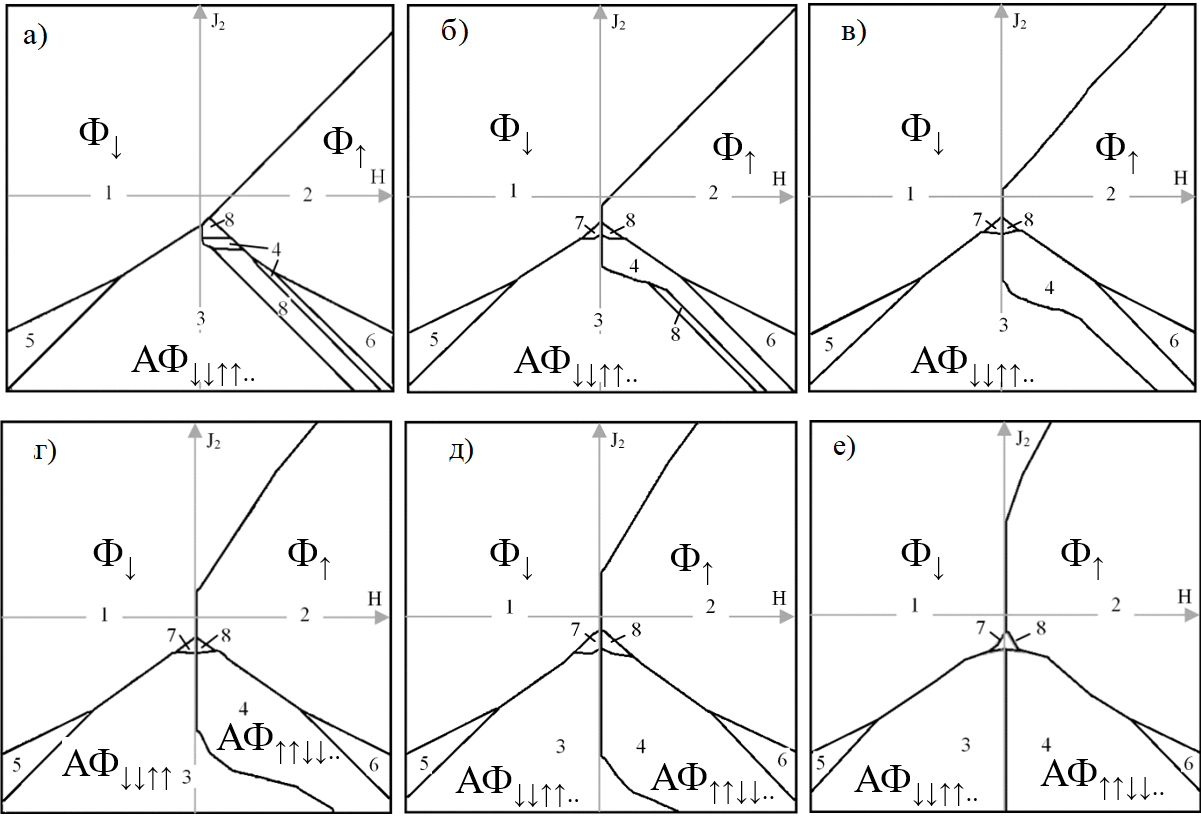
Рисунок 2 - Диаграммы малой магнитной системы в осях J2-H при возрастании температуры:

а – Т=0,1; б – Т=0,3; в – Т=0,5; г – Т=0,8; д – Т=1; е – Т=1,5

DOI:10.23670/IRJ.2022.126.56.2

В области 8 формируется антиферромагнитная область 4 и с ростом температуры вытесняет ее (область 8) в положение характерное для диаграммы основного состояния. Формируется область 7. Далее область 4 расширяется влево до прямой Н=0. За счет увеличения тепловых колебаний атомов уменьшается запаздывание в перестройке спинов из фазы 1 в фазу 2, т.е частице проще преодолеть потенциальный барьер. С увеличением температуры наблюдается уменьшение переходных областей 5 и 6 за счет стабилизации антиферромагнитных областей 3 и 4. При температуре больше Т=1,5 наблюдается размытие границ между фазами – тепловое движение разрушает порядок.

Феномен многоспинового обмена был предсказан в работах Боголюбова [10] и были попытки его учета в виде трехчастичного взаимодействия. Но ввиду инвариантности гамильтониана относительно инверсии спинов следует в вопросах магнетизма предполагать, что низший порядок многоспинового взаимодействия четырехчастичный ~ S1S2S3S4. Проследим влияние данного взаимодействия на фазовые диаграммы при температуре Т=1 (рис. 3).

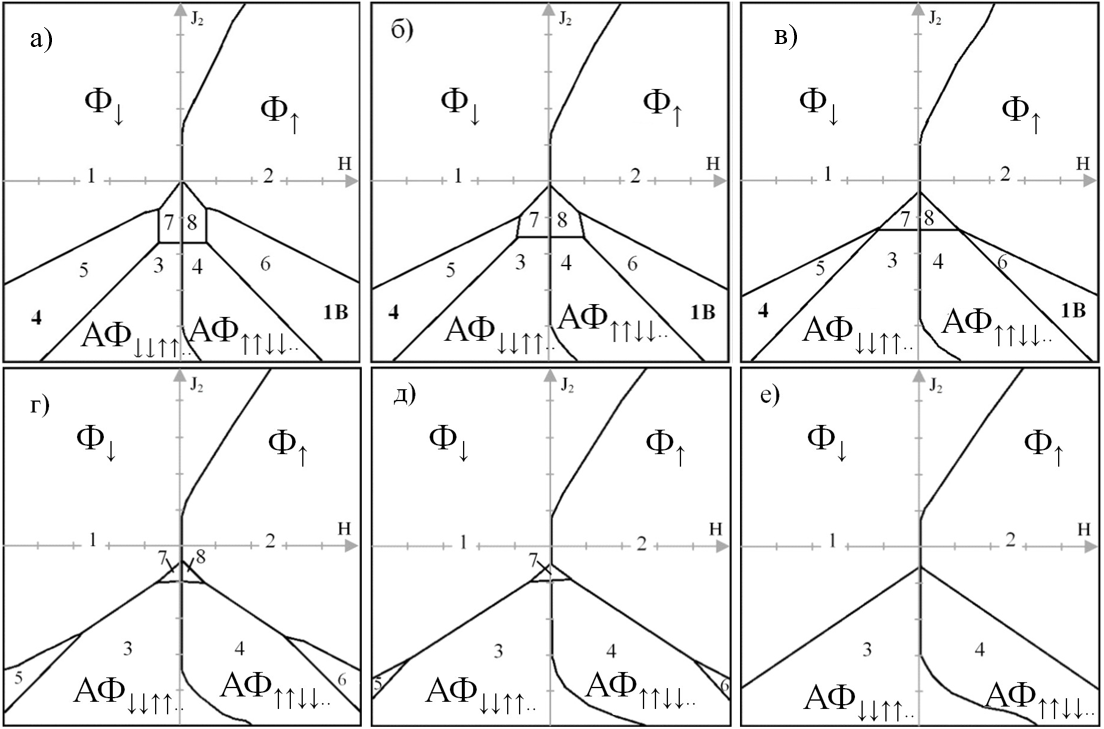
Рисунок 3 - Динамика вырождения магнитных структур в кристаллах:

а – J1-4=-0,7; б – J1-4=-0,5; в – J1-4=-0,3; г – J1-4=0,01; д – J1-4=0,2; е – J1-4=0,5

DOI:10.23670/IRJ.2022.126.56.3

Увеличение энергии четырехчастичного взаимодействия приводит к размытию и дальнейшему исчезновению областей 7 и 8, также уменьшаются области 5 и 6 и при J1-4>0,4 не реализуются. При достаточно большой энергии четырехчастичного взаимодействия в системе существуют только ферромагнитные и антиферромагнитные фазы.

Проанализируем изменения происходящие с диаграммами при учете температуры по сравнению с ДОС для аналогичных параметров: различия в реализуемых магнитных конфигурациях минимальна и заключаются в искривлении границ на фазовых диаграммах вблизи прямой Н=0, а также тем, что на диаграммах основных состояний переходные области 5 и 6 незначительно больше (увеличение за счет антиферромагнитных областей).

При отрицательных значениях четырехчастичного взаимодействия на фазовых диаграммах наблюдается значительное расширение переходных дефектных антиферромагнитных областей 3 и 4, 5 и 6 по сравнению с диаграммами, не учитывающими дальнего и четырехчастичного взаимодействия. Кроме этого, смена магнитной структуры при изменении знака напряженности внешнего магнитного поля происходит быстрее для веществ с отрицательной энергией четырехчастичного взаимодействия.

Таким образом, наличие в образце четырехчастичного взаимодействия существенно влияет на устойчивость магнитных фаз. Подбирая параметр J1-4 можно либо стабилизировать переходные области между ферромагнитными и антиферромагнитными фазами, тем самым затрудняя переход между ними, либо наоборот свести эти области к минимуму или исключить полностью, делая возможным непосредственный переход между ферромагнитными и антиферромагнитными фазами при любых значениях J2.

Проанализировав магнитные структуры фазовых диаграмм и диаграмм при абсолютном нуле, можно утверждать, что температура оказывает существенное влияние на стабильность магнитных фаз, возникают новые типы магнитных превращений и нарушается «зеркальность» фаз относительно изменения знака внешнего магнитного поля (наблюдаются гистерезисные явления). Также метод построения фазовых диаграмм при конечных температурах позволяет выявить метастабильные фазы, отсутствующие на диаграммах основных состояний. Учет четырехчастичного взаимодействия спинов приводит к полному вырождению дефектных антиферромагнитных конфигураций, следовательно, материалы, в которых данное взаимодействие составляет порядка половины от J1 будут представлены единой доменной структурой. На основе анализа фазовых диаграмм при конечной температуре, мы можем определить при каких энергетических параметрах стабильна интересующая нас фаза при определенной температуре. И рассмотреть критические показатели для определенного типа магнетика.