TUTORIAL AND SOFTWARE ENVIRONMENT: CALCULATION, SIMULATION ON A COMPUTING DEVICE AND TESTING OF NONRECURSIVE DIGITAL FILTERS
TUTORIAL AND SOFTWARE ENVIRONMENT: CALCULATION, SIMULATION ON A COMPUTING DEVICE AND TESTING OF NONRECURSIVE DIGITAL FILTERS
Abstract
The state educational standards of the last generation require students to form knowledge and skills in the subject area under study. The experience of "Electrical Engineering and Electronics" discipline has shown that it is possible to meet these requirements only with the use of software or simulators, due to the sharp reduction in the curriculum (in some bachelor's degree programs by half) both the total volume of hours to study the discipline, and the hours in it for classroom studies.
To provide students in all forms of education with these tools at the Department of MAI developed electronic resources (more than a dozen of them are registered) with the participation of students in their project work on the author's algorithms for use in all types of classes in the discipline.
The article reviews the freely distributed DNF learning and software environment for modelling nonrecursive digital filters to install it on the laptops of students pursuing a particular specialization in engineering and technology. Individualization of assignments for designing a filter with (self-)control of its stages, as well as consultations (in person or remotely), stimulate the work of students in the semester, and despite the uneven study discipline in the semester for various reasons to 15-20% of students in the groups who have not completed term papers on time, one or two students remain, mostly for a valid reason.
1. Введение
Вследствие невозможности выполнения вручную из-за больших затрат на вычислительные процедуры и графические построения характеристик, проектирование и испытание цифровых устройств обработки сигналов проводят в программных средах типа Mathcad, Delta Design и др. [1].
В связи с уменьшением объема часов на изучение электротехники и электроники и на планирование курсовых работ по дисциплине в учебных планах многих направлений бакалавриата в области техники и технологий, преподаватель теперь проводит занятия в 5-6 группах: с 80-90 студентами в семестре, из которых 15-20 % по разным причинам нерегулярно изучают дисциплину. В этих условиях выполнение студентами заданий или курсовых работ в семестре в установленные сроки помогла бы (практически не реализуемая на практике) установка на их ВУ (ноутбук, планшет и др.) лицензионной среды моделирования и анализа электронных устройств.
В данной статье рассматриваются методологические основы проектирования нерекурсивных цифровых фильтров (НЦФ), а также разработка учебно-программной среды DNF [2] для расчета, моделирования и испытания НЧФ нижних частот по заданным параметрам к его амплитудно-частотной характеристике (АЧХ). Среда DNF разработана с использованием языков Visual C++ 6.0 и DHTML для инсталляции на студенческие ВУ с ОС Windows 10 или 11, с браузером Edge и объемом свободной памяти не менее 20 МБ.
Цифровой фильтр - дискретная система, преобразующая последовательность x(k) отсчётов входного сигнала в последовательность y(k) отсчётов выходного сигнала. Среди фильтров выделяют нерекурсивные (КИХ-фильтры) и рекурсивные (БИХ-фильтры) соответственно с конечными и с бесконечными импульсными характеристиками, а по расположению частотных полос пропускания и задержки сигналов их подразделяют на фильтры нижних и верхних частот, полосовые и заграждающие (режекторые) [3], [4] и [5].
Цифровые фильтры используют для цифровой фильтрации и спектрального анализа сигналов [6]: в радиолокации, в медицинской аппаратуре, в каналах связи телекоммуникаций для передачи информации и т.п.
В учебных планах подготовки инженеров уделено большое внимание изучению процессов цифровой обработки сигналов, в частности, расчёту и моделированию цифровых систем для их преобразования [7], [8] и [9].
2. Методы и принципы исследования
Работа основана на изучении литературы по данной теме и анализе личного многолетнего опыта преподавания электротехнических дисциплин.
Проектирование НЦФ нижних частот выполнялось на основе аппроксимации заданной идеальной АЧХ фильтра модифицированным гармоническим рядом Фурье (метод «окон») [1], [10].
Разработка ПО учебно-программной среды DNF проводилась с использованием языков Visual C++ 6.0 и DHTML.
В реализации НЦФ в виде программы для ВУ использовалась прямая структурная схема, построенная на базе трех типов электронных элементов: сумматоров, умножителей и элементов задержки.
Проверка функциональных возможностей синтезированного НЦФ проводилась по стандартной методике посредством подачи на его вход типовых (тестовых) сигналов: единичного отсчета, единичной последовательности, дискретизированных синусоидального и косинусоидального сигналов.
Проверка значений выходных отсчетов сигналов фильтра, рассчитанных по подпрограмме DNF, выполнялась по их равенству выходным отсчетам, найденных вручную посредством операции свертки двух сигналов: подаваемой на вход фильтра четырехточечной последовательности отсчетов, задаваемых вручную с клавиатуры ВУ, с дискретной импульсной функцией НЦФ.
3. Основные результаты
Алгоритмы фильтрации, структурные схемы и характеристики НЦФ
Главной характеристикой линейного НЦФ, работающего во временной области, является алгоритм фильтрации, описываемый линейным разностным уравнением N-го порядка
где ,
- постоянные фильтра;
- номер отсчёта входной последовательности (сигнала)
;
и
- шаг и частота дискретизации аналогового сигнала.
Максимально допустимый шаг , соответственно минимальную частоту
дискретизации входного сигнала
, выбирают на основе теоремы отсчётов (теоремы Котельникова) [1, C. 57]:
где - максимальная частота спектра сигнала
, определяемая на основе, например, энергетического критерия.
В общем случае выходной сигнал (при
) в текущий момент времени
определяется значением входного сигнала
в тот же момент времени
, значениями входного сигнала в предшествующие моменты времени
и описывается разностным уравнением вида
где - задержанный соответственно на n отсчётов входной сигнал.
Варьируя величинами и
в уравнении (1) или (2), создают набор алгоритмов для реализации структуры схемы фильтра на базе трех типов электронных элементов: сумматоров (условное обозначение на схемах
), умножителей
и элементов задержки
.
Системную функцию прямой структуры НЦФ (рис. 1, а), выражающую соотношение между выходными
и входными
дискретными сигналами, обычно выражают в
-области, т.е.
где ,
- комплексная частота (в рад/с),
,
а в каскадной структуре, состоящей из звеньев 2-го порядка (рис. 1, б),
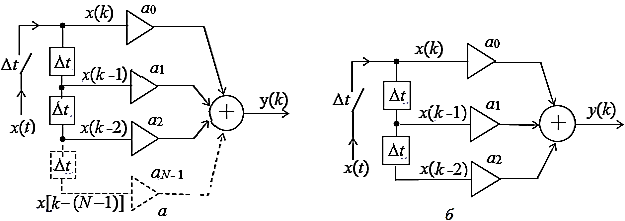
Рисунок 1 - Прямая структурная схема НЦФ (а) и структурная схема звена 2-го порядка (б)
Системная функция фильтра в частотной области
является прямым z-преобразованием импульсной функции фильтра, которая, в свою очередь, равна обратному преобразованию системной функции:
Интегрирование выражения (7) обычно ведут по контуру единичного радиуса, при котором подставив которое в (3) получают комплексную передаточную функцию НЦФ:
или
где и
- модуль и аргумент комплексной передаточной функции, называемые соответственно амплитудно-частотной (АЧХ) и фазо-частотной (ФЧХ) характеристиками фильтра.
Из выражения (9) следует, что характеристики АЧХ и ФЧХ НЦФ являются периодическими функциями частоты с периодом, равным частоте дискретизации
, и определяются весовыми коэффициентами в прямых
связях схемы НЦФ (см. рис. 1, а), а также шагом дискретизации
(рис. 2, а), поэтому требования к ним достаточно задавать на интервале угловых частот
, а для построении графика модуля
АЧХ фильтра в диапазоне от 0 до
- при изменении угла
от 0 до
.
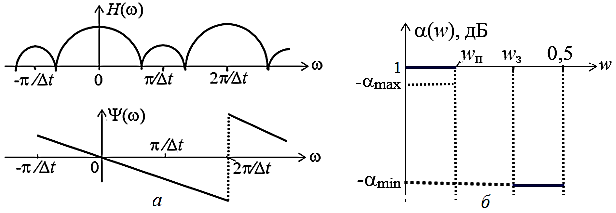
Рисунок 2 - Частотные характеристики АЧХ H(ω) и ФЧХ Ψ(ω) НЦФ (а) и границы полос пропускания wп и задерживания wз(б)
где - относительная циклическая частота НЦФ.
Тогда требования к частотным характеристикам фильтра следует задавать на интервале w = [0…0,5], а реальная шкала частот равна f = wfд. При этом изменяются аргументы в обозначениях характеристик: ,
,
.
Методы расчета НЦФ с заданными требованиями к АЧХ
Для разработки учебно-программной среды DNF, с помощью которой по заданным параметров АЧХ можно определить минимальный порядок N НЦФ нижних частот, синтезировать его и провести анализ его временных и частотных характеристик, необходимо выбрать метод расчета параметров НЦФ нижних частот и получить математические выражения его характеристик.
Метод расчёта НЦФ с заданной идеальной АЧХ связан с выбранным из сгруппированных в три группы [1] критерием ее аппроксимации. Первая группа включает метод разложения в ряд Фурье и метод наименьших квадратов, вторая и третья – алгоритм Ремеза и некоторые другие сравнительно редко используемые алгоритмы.
Выбираем метод разложения в ряд Фурье, так как для его реализации требуется наименьший объём вычислений, особенно при числе отсчетов N > 5000…10000.
Комплексный ряд Фурье [1, С. 238] периодической функции
при нечётном
и симметричных коэффициентах
(рис. 3, а)
где коэффициенты ряда Фурье ck (рис. 3, б)
а соответствующий ряд Фурье
Выполнив замену переменных в (12) при , получим ряд Фурье
с коэффициентами ck, совпадающими с отсчётами функции g(k) фильтра.
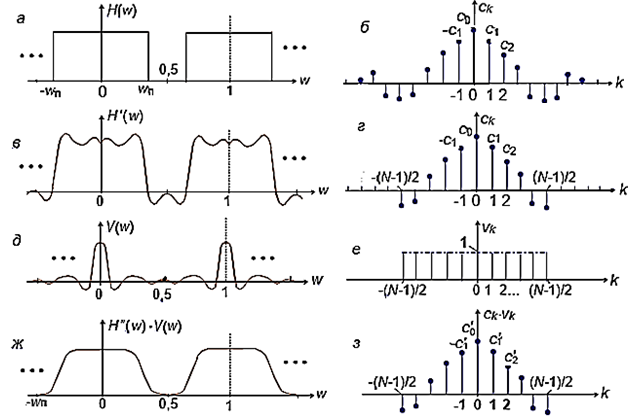
Рисунок 3 - Графики функций при поэтапном выводе выражения системной функции НЦФ по заданной АЧХ при ее аппроксимации модифицированным рядом Фурье
Однако простое усечение ряда Фурье приводит к явлению Гиббса, которое проявляется на графике АЧХ в виде выбросов (до 9%) в зоне пропускания сигнала и пульсаций АЧХ (рис. 3, в). Увеличение числа N не уменьшает максимальную амплитуду пульсаций, а уменьшает лишь ширину выбросов.
Чтобы исключить явление Гиббса, коэффициенты сk ряда Фурье (см. рис. 3, г) умножают на множители прямоугольной весовой функцию v(k) (рис. 3, е) с передаточной функцией V(w) (рис. 3, д) при и на нуль при |k| > L. Этот процесс приводит к сглаживанию передаточной функции (рис. 3, ж). При использовании других весовых функций («окон»): треугольного «окна», функций Хемминга, Блэкмана или Кайзера уменьшается колебательный характер у окончательной передаточной функции, но одновременно увеличивается ширина промежуточной полосы.
Для физической реализации НЦФ ограниченную последовательность коэффициентов сk Фурье (см. рис. 3, г) сдвигают вправо на L отсчётов и рассчитывают комплексную передаточную функцию по формуле
а после умножения ее коэффициентов сk на коэффициенты функции vk получают модифицированную передаточную функцию
где L = (N-1)/2; ak - коэффициенты импульсной функции g(k) фильтра, определяемые по формулам: a0 = с'L, aL = с'0; аk = с'L- k, k = 1, 2,…, L.
Если выполняется условие ak=aN-k-1, то ФЧХ НЦФ
т.е. ФЧХ нерекурсивного фильтра является линейной периодической функцией c областью определения для циклической частоты w от -0,5 до 0,5 со скачком на графике ФЧХ от до
на границе указанного диапазона.
Полученные выражения (10)…(16) использованы при разработке ПО среды DNF, в которой вычисления ведутся с числами конечной длины, определяемой разрядностью микропроцессора типа Pentium, равной 64 битам (вычисления ведутся с двойной точностью), что позволяет не проводить анализ влияния ограничений разрядности чисел на точность выходных отсчетов.
Проектирование НЦФ c заданными требованиями к его АЧХ
Из проведенного выше анализа следует, что расчет НЦФ сводится к определению коэффициентов правых частей уравнений (2) или (3) по заданным требованиям к его АЧХ в несколько этапов:
· анализ требований к АЧХ фильтра;
· формулировка задачи аппроксимации заданной его АЧХ;
· схемная реализация фильтра;
· проверка работоспособности синтезированного фильтра: он должен быть устойчивым и физически реализуемым.
Исходными данными для расчёта ЦФ являются граничные частоты и
полос пропускания и задерживания, допуски
(в дБ) на отклонение АЧХ от номинального уровня (равного единице) в полосе пропускания и
(в дБ) в полосе задерживания (см. рис. 2, б), а также частота дискретизации входного аналогового сигнала
.
Требования к АЧХ НЦФ при решении задачи ее аппроксимации обычно трансформируются в требования к его коэффициенту затухания (в дБ):
т.е. исходными данными являются: максимальное отклонение коэффициента затухания от номинального уровня в полосе пропускания
и гарантированное затухание сигнала в полосе
.
Прежде чем начать проектирование НЦФ, студент должен изучить материалы лекций по цифровой обработке сигналов, методику расчета НЦФ и пройти «Опрос по теме» (рис. 4), правильно ответив на ³75 % тестовых заданий.

Рисунок 4 - Фрагменты тестовых заданий

Рисунок 5 - Главное меню учебно-программной среды DNF
- New (проектирование нового НЦФ),
- ЦФ (заставка для ввода параметров ЦФ),
- АЧХ (вывод на экран графика АЧХ фильтра),
- ЛАЧХ (вывод на экран графика логарифмической АЧХ фильтра),
- ФЧХ (вывод на экран графика логарифмической ФЧХ фильтра),
- ИХ (вывод на экран графика импульсной характеристики фильтра),
- ВО (вывод на экран графика весового окна),
- Тест (вывод на экран заставки для выбора тестовых сигналов и ввода их параметров),
- ВхС (вывод на экран графика тестового входного сигнала),
- ВыхС (вывод на экран графика выходного сигнала фильтра),
- About (информация о разработчиках ПО среды DNF).
Проектирование НЦФ начинается со щелчка мышью на кнопке «New» в главном меню среды DNF. При этом всплывает окно «ЦФ» (рис. 6, а) ввода исходных данных для проектирования, например, варианта 1 (табл. 1) фильтра.
Вначале, посредством щелчка мышью на кнопке «ЛАЧХ» на экран дисплея ВУ выводится окно с графиком ЛАЧХ фильтра (рис. 6, б), а после щелчка мышью на кнопке «Enter» клавиатуры ВУ и ввода значений частот wп и wз в окна «Частота 1» и «Частота 2», выводятся значения коэффициентов и
при заданном порядке, например, N = 17 фильтра.
Так как полученные коэффициенты и
меньше заданных:
то порядок N фильтра необходимо увеличить, щелкая каждый раз мышью с его увеличением на кнопках «Запомнить» и «ЛАЧХ» в меню среды DNF для автоматического обновления как графика ЛАЧХ, так и ниже него значений новых коэффициентов.
Таблица 1 - Исходные данные для проектирования НЦФ нижних частот
Номер варианта | fn, кГц | fi, кГц | αmax, дБ | αmin, дБ | fz, кГц | Номера «окон» | Входной четырехточечный сигнал |
1 (16) | 4,8 | 19,2 (9,6) | -0,1 | -40 | 48 | 1 и 3 | {2, -1, -2, 1} |
2 (17) | 2,4 | 4,8 (9,6) | -0,2 | -50 | 48 | 1 и 2 | {-1, 1, -2, 2} |
3 (18) | 2,4 | 9,6 (19,2) | -0,3 | -40 | 48 | 1 и 4 | {-2, -1, 1, 2} |
4 (19) | 2,0 | 6,0 (8,0) | -0,4 | -50 | 48 | 1 и 2 | {1, 2, -1, -2} |
5 (20) | 1,6 | 6,4 (9,6) | -0,5 | -40 | 32 | 1 и 3 | {1, 2, -2, 1} |
6 (21) | 2,0 | 5,0 (6,0) | -0,1 | -50 | 32 | 1 и 4 | {1, 1, 1, 1} |
7 (22) | 2,0 | 6,0 (8,0) | -0,2 | -40 | 32 | 1 и 2 | {1, 1, 2, 1} |
8 (23) | 3,2 | 6,4 (9,6) | -0,3 | -50 | 24 | 1 и 3 | {1, 2, 1, 1} |
9 (24) | 2,4 | 7,2 (9,6) | -0,4 | -40 | 24 | 1 и 4 | {-1, 1, -1, 1} |
10 (25) | 2,0 | 4,0 (6,0) | -0,5 | -50 | 24 | 1 и 2 | {1, -1, 1, -1} |
11 (26) | 2,4 | 8,0 (10,0) | -0,1 | -40 | 40 | 1 и 3 | {2, 1, 1, 2} |
12 (27) | 2,4 | 5,0 (8,0) | -0,2 | -50 | 40 | 1 и 4 | {2, 2, 1, 1} |
13 (28) | 4,8 | 9,6 (6,0) | -0,3 | -40 | 48 | 1 и 2 | {2, 1, 2, 1} |
14 (29) | 4,8 | 19,2 (9,6) | -0,4 | -50 | 48 | 1 и 3 | {1, 1, 1, -1} |
15 (30) | 3 | 6,0 (9,0) | -0,5 | -40 | 30 | 1 и 4 | {1, -1, 1, 1} |
Наконец, при N = 31 (рис. 6, г) требования к АЧХ выполнены и даже перевыполнено требование для в полосе пропускания:
вследствие необходимости обеспечить второе требование к АЧХ: коэффициент ç-aminç должен быть равен или больше 40 дБ.
После выбора окна «Хемминга» (см. рис. 6, в) и щелчка мышью на кнопках «ВО» и «ЛАЧХ», на экран ВУ выводится график выбранного окна (рис. 6, д) и график LАЧХ (рис. 6, е), на котором видно, что границы полос пропускания и задерживания «размылись» и расширилась переходная полоса wз-wп, что свидетельствует о снижение разрешающей способности фильтра при одновременном уменьшении пульсаций АЧХ в полосе пропускания и лучшем их подавлении в полосе задерживания.
Графики АЧХ фильтра (рис. 6, ж) и его импульсной функции g(k) (рис. 6, з) выведены на экран дисплея ВУ посредством щелчков мышью на кнопках «АЧХ» и «ИХ» главного меню среды DNF. Значения коэффициентов ak центральной части импульсной характеристики g(k), выведенные слева от ее графика, равны:
a15 = 0,5; a14 = a16 = 0,27324; a13 = a17 = 0; a12 = a18 = -0,011 и т.д.
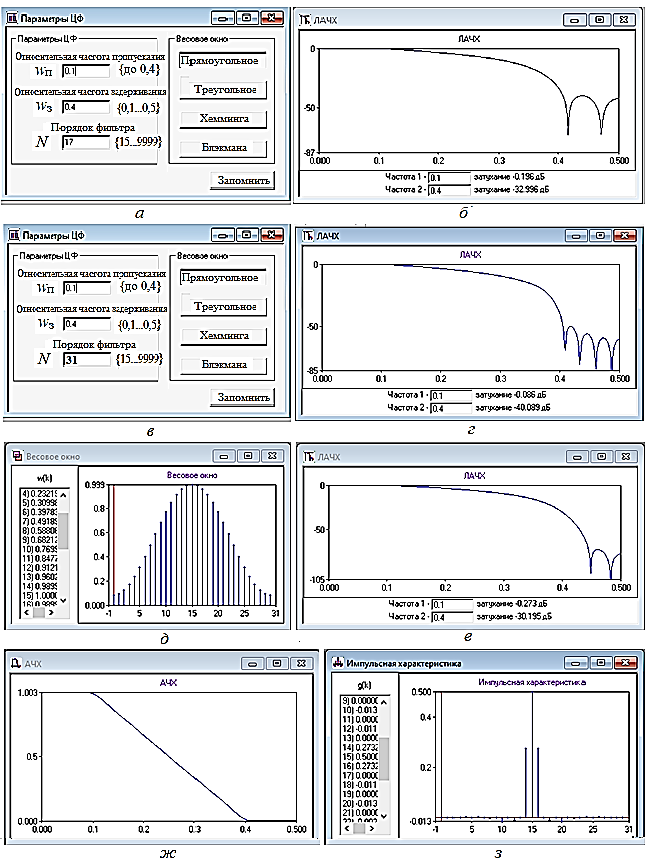
Рисунок 6 - Заставки среды DNF (а, в) и графики характеристик НЦФ:
б - ЛАЧХ при N=17; г - при N= 31; е- с окном Хемминга; д - окна Хемминга; ж- АЧХ; з- ИХ
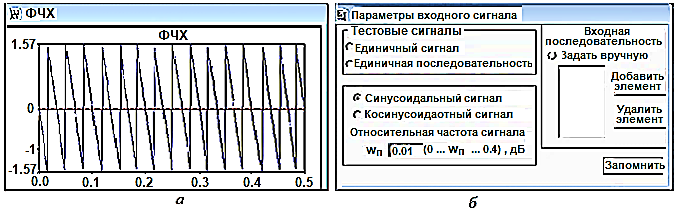
Рисунок 7 - График ФЧХ спроектированного НЦФ (а) и заставка (б) для выбора и ввода тестовых сигналов в подпрограммы среды DNF
Обобщенная структурная схема прямой структуры спроектированного НЦФ аналогична схеме (см. рис. 1, а), с изменением в ней только записи последнего коэффициента на . Запишем выражения системной функции
и импульсной функции фильтра
Проверка нерекурсивных ЦФ на устойчивость не проводится, так как они принципиально устойчивые.
Испытание синтезированного НЦФ
При разработке цифрового фильтра в виде специального устройства на базе сигнального процессора типа TSP-320хх и др. предварительно выполняют его синтез в виде программы на базе микропроцессора ВУ и анализируют графики выходных характеристик, полученных посредством подачи на его вход следующих тестовых сигналов: единичного отсчета, единичной последовательности, дискретизированных синусоидального и косинусоидального сигналов, произвольной последовательности отсчетов, задаваемой вручную с клавиатуры ВУ, и, реже, полигармонический синусоидальный сигнал для демонстрации его цифровой фильтрации.
После щелчка мышью на кнопке «Тест» в выведенной на экран заставке (см. (рис. 7, б) выбирают входные сигналы, последовательно подают их на вход НЦФ и выводят на экран ВУ графики входных и выходных сигналов посредством щелчков мышью на кнопках «ВхС» и «ВыхС»:
а) при подаче на вход единичного отсчёта на выходе НЦФ получают импульсную функцию ИХ g(k) фильтра (см. рис. 6, з), на графике которой видны ярко выраженные отсчеты в центральной ее части (a15 = 0,5, a14 = a16 = 0,27324) и резкое снижение коэффициентов ak при удалении от ее центральной части;
б) далее, при подаче на вход фильтра единичной последовательности (рис. 8, а) на экран ВУ выводится график переходной функции h(k) (рис. 8, б), время установления которой (от 0 до 0,9 уровня 1) равно
;
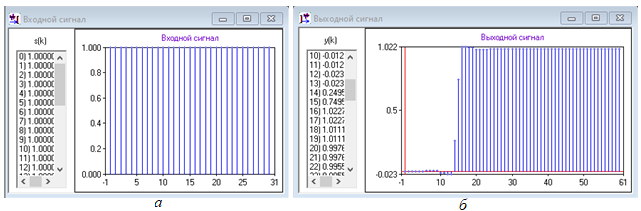
Рисунок 8 - Единичная последовательность (а) и переходная характеристика h(k) (б) НЦФ
На рис. 9, б и рис. 10, б представлены графики выходных сигналов с нормированной частотой w = 0,01, на которых заметны 1/w = 100 отсчетов за период, задержка выходных сигналов на L = 15 отсчетов и заметное искажение первой полуволны косинусоидального сигнала;
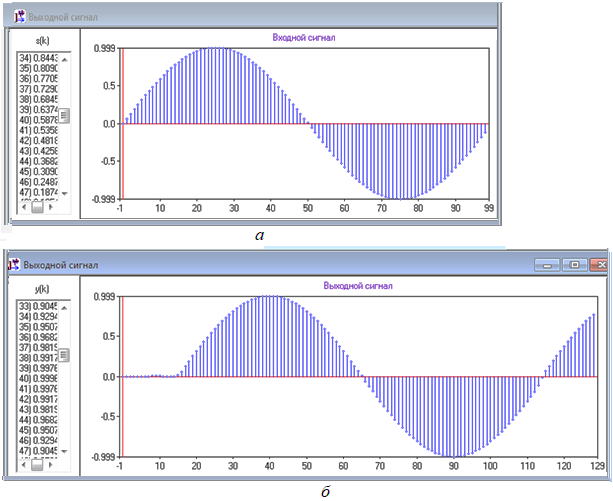
Рисунок 9 - График входного синусоидального сигнала (а) и его график на выходе НЦФ (б)
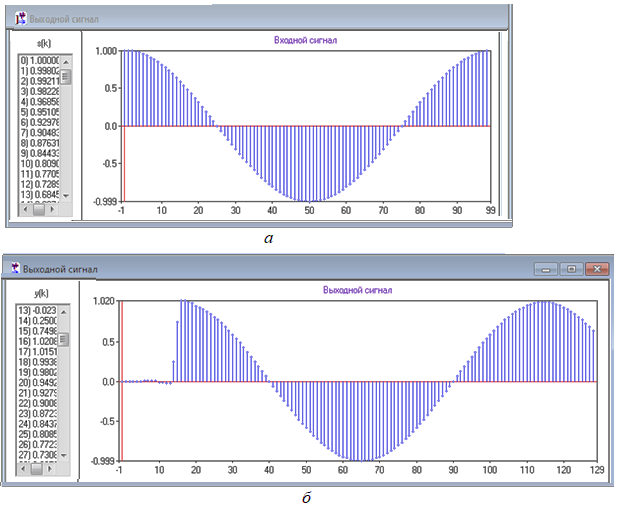
Рисунок 10 - График входного косинусоидального сигнала (а) и его график на выходе НЦФ (б)
операции свертки двух дискретных сигналов: четырехточечной последовательности х(k) = {2, -1, -2, 1}, введенной вручную с клавиатуры ВУ и поданной на вход фильтра (рис. 11, а), и импульсной функции g(k) (см. рис. 6. з) фильтра, посредством сравнения с рассчитанными вручную значениями отсчетов операции свертки указанных сигналов х(k) и g(k) при k = L= 15, L + 1 = 16 и L + 2 = 17 следующим образом [1, C. 136]:
· отсчеты входного сигнала записывают в обратном направлении, т.е.
· выписывают в одну строку значения отсчетов, например, а11…а19 импульсной характеристики g(k) (см. рис. 6, з, слева);
· размещают полученную последовательность отсчетов х(-k)= {1, -2, -1, 2} ниже строки с последовательностью отсчетов центральной части импульсной функции g(k) фильтра таким образом, чтобы отсчет х0 оказался напротив центрального отсчета L15;
- вычисляют значение выходного отсчета
значения отсчетов y16 ≈ - 0,5 и y17 ≈ -1 определены посредством cуммирования произведений соответствующих значений x(k) и значений отсчетов импульсной функции фильтра g(k) при сдвиге вправо на один и два шага последовательности {1, -2, -1, 2}.
Количества всех отсчетов выходного сигнала в данной свертке сигналов
(см. рис. 11, б),
где N = 31 - число отсчетов импульсной функции g(k); Х = 4 - число отсчетов входного сигнала x(k).
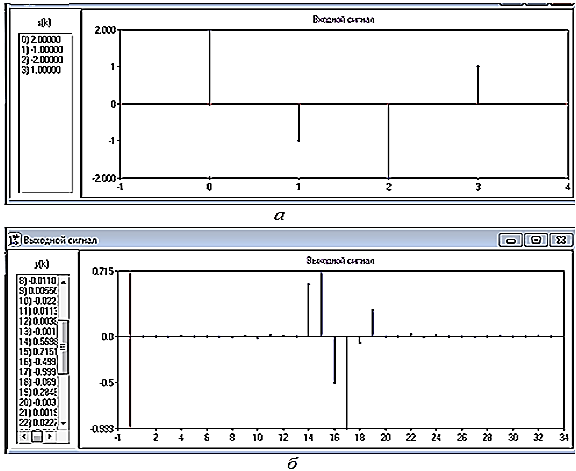
Рисунок 11 - Графики входной последовательности x(k) (а) и последовательности выходных отсчетов y(k) свертки входного сигнала x(k) и ИХ g(k) НЦФ (б)
4. Заключение
Разработан свободно распространяемый электронный ресурс (учебно-программная среда DNF с требуемым объемом памяти для установки 20 МБ) для проектирования цифровых нерекурсивных фильтров и анализа выводимых на экраны ВУ студентов его графиков временных и частотных характеристик.
В сравнение с лицензионными средами типа Mathcad и др., используемые студентами на кафедрах вуза, и на освоение которых требуется определенное время, затраты же времени на освоение среды DNF, предназначенной для инсталляции на ВУ студентов, сведены к минимуму: она имеет простой и понятный интерфейс, выполненный в виде одной командной строки кнопок. После щелчка мышью на каждой из них на экран дисплея ВУ выводится заставка для ввода исходных данных или график соответствующей характеристики синтезированного в виде программы НЦФ.
Разработаны варианты заданий на проектирования НЦФ; приведен пример расчета одного из вариантов, а также синтез структурной схемы фильтра и его испытание по стандартной методике с подачей на его вход тестовых сигналов и анализом выводимых на экран ВУ графиков характеристик фильтра.
Представлен подробный вывод формулы модифицированного ряда Фурье с построением графиков получаемых временных и частотных промежуточных функций, используемых студентами для сравнения с видом графиков характеристик спроектированных фильтров при их анализе.
Наличие программной среды DNF обуславливает выполнение курсовых работ в удобное студентам время и их защиту в установленный срок, а невыполненные курсовые работы в срок одним или двумя студентами в группах вызваны, в основном, уважительными причинами.
Программная среда DNF включена в программный комплекс УМК-Э2 по электронике [8] и используется преподавателями для демонстрации ее фрагментов на лекциях и практических занятиях при любом нечетном числе порядка фильтра N (вплоть до 9999 и более).
