BOUNDARY LINES OF ANALYTIC FUNCTIONS WITH A PARAMETER
ПОГРАНИЧНЫЕ ЛИНИИ АНАЛИТИЧЕСКИХ ФУНКЦИЙ С ПАРАМЕТРОМ
Научная статья
Алыбаев К.С.1, Нарымбетов Т.К.2, *
1 ORCID: 0000-0002-7962-534X;
2 ORCID: 0000-0003-0921-4542;
1 Жалал-Абадский государственный университет, Жалал-Абад, Кыргызстан;
2 Научно-исследовательский медико-социальный институт, Жалал-Абад, Кыргызстан
* Корреспондирующий автор (talant83[at]mail.ru)
АннотацияИсследование различных процессов (электрических и магнитных полей, течение воздуха и жидкостей, квантовой физики и т.д.) сводятся к исследованию аналитических функций комплексного переменного. Объектом исследования данной работе являются аналитические функции комплексного переменного с параметром. Для таких классов функций вводятся понятия пограничная, регулярная, сингулярная точки. Далее определены понятия: сингулярная, регулярная и пограничная области. С использованием топологического подхода вводится более широкое понятие пограничной линии. Из множества пограничных линий выделяется главная пограничная линия, и на примерах показаны топология и разнообразные формы главных пограничных линий (замкнутая, паукообразная, с проколотой точкой, счетное количество), структура пограничной области. Как показывают примеры, для общего случая невозможно определить формы главных пограничных линий и каждый случай надо рассмотреть отдельно.
Ключевые слова: аналитическая функция, пограничная точка, пограничная линия, главная пограничная линия, пограничная область, регулярные и сингулярные области, гармонические функции, линии уровня.
BOUNDARY LINES OF ANALYTIC FUNCTIONS WITH A PARAMETER
Research article
Alybaev K.C.1, Narymbetov T.K.2, *
1 ORCID: 0000-0002-7962-534X;
2 ORCID: 0000-0003-0921-4542;
1 Jalal-Abad State University, Jalal-Abad, Kyrgyzstan;
2 Medical and Social Research Institute, Jalal-Abad, Kyrgyzstan
* Corresponding author (talant83[at]mail.ru)
AbstractThe study of various processes (electric and magnetic fields, the flow of air and liquids, quantum physics, etc.) comes down to the study of analytical functions of a complex variable. The subject of research is the analytic functions of a complex variable with a parameter. The research introduces the concepts of boundary, regular, and singular points for such classes of functions and defines the following concepts: singular, regular, and boundary regions. Using the topological approach, the study broadens the concept of a boundary line. The study selects the main boundary line from the set of boundary lines. The examples illustrate the topology and various forms of the main boundary lines (closed, spider-like, with a punctured point, a countable amount) as well as the structure of the boundary area. As shown in the examples throughout, it is impossible to determine the shape of the main boundary lines for the general case, therefore each case must be considered separately.
Keywords: analytic function, boundary point, boundary line, main boundary line, boundary region, regular and singular domains, harmonic functions, contour line.
Вводная частьВ работах [1], [4], [7] при исследовании асимптотического поведения решений сингулярно возмущенных обыкновенных дифференциальных уравнений использованы пограничные линии, регулярные и сингулярные области. При этом пограничные линии определены как прообраз прямолинейного отрезка, и они разделяют только регулярные и сингулярные области. При этом в перечисленных работах не исследованы топология пограничных линий их различные формы и структура пограничных областей.
Необходимые определения
Пусть задана скалярная функция ![]() , где t - комплексная переменная,
, где t - комплексная переменная, ![]() - малый вещественный параметр.
- малый вещественный параметр.
Будем предполагать ![]() - аналитическая функция по переменной t в некоторой односвязной области
- аналитическая функция по переменной t в некоторой односвязной области ![]() . Пусть t0 внутренняя точка области D.
. Пусть t0 внутренняя точка области D.
Определение 1. Если предел ![]() не существует, но
не существует, но ![]() ограничена, то будем говорить, точка t0 является пограничной точкой.
ограничена, то будем говорить, точка t0 является пограничной точкой.
Определение 2. Если предел ![]() существует, то t0 назовём регулярной точкой.
существует, то t0 назовём регулярной точкой.
Определение 3. Если предел ![]() , то t0 назовём сингулярной точкой.
, то t0 назовём сингулярной точкой.
Определение 4. Множество пограничных точек назовём пограничной областью.
Определение 5. Множество регулярных точек назовём регулярной областью, а множество сингулярных точек сингулярной областью.
Определение 6. Одномерное связное (по Урысону) и одновременно компактное множество пограничных точек назовём пограничной линией.
Топология пограничных линий
Далее все рассматриваемые кривые состоят из простых дуг, порождаемых гармоническими функциями. Если такие кривые состоят из пограничных точек, то, согласно определению 6, они являются пограничными линиями.
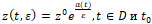 и является простым нулем функции
и является простым нулем функции 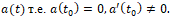
При таком предположении через точку t0 проходят единственные линии уровня гармонических функций ![]() . Эти линии определяются уравнениями
. Эти линии определяются уравнениями ![]() причем они являются взаимно ортогональными [8].
причем они являются взаимно ортогональными [8].
Линия ![]() некоторую окрестность точки делить на две части [9]. Рассматриваемую окрестность обозначим
некоторую окрестность точки делить на две части [9]. Рассматриваемую окрестность обозначим ![]() причем линия
причем линия ![]()
Функцию ![]() рассмотрим вдоль линии
рассмотрим вдоль линии ![]() . Вдоль этой линии функция
. Вдоль этой линии функция ![]() строго монотонна [9]. Поскольку
строго монотонна [9]. Поскольку ![]() то в каждом из частей
то в каждом из частей ![]() принимает либо положительные, либо отрицательные значения. Для определенности возьмём
принимает либо положительные, либо отрицательные значения. Для определенности возьмём
![]()
Пусть ![]() Отсюда вытекает, что предел
Отсюда вытекает, что предел ![]() не существует, но
не существует, но ![]() ограничена. Следовательно кривая
ограничена. Следовательно кривая ![]() пограничная линия, согласно определению 6.
пограничная линия, согласно определению 6.
1.2. Пусть в точке t0 функция a(t) имеет n кратный нуль. Тогда некоторая окрестность точки t0 линией ![]() разделяется на 2n частей, при этом в каждом из частей функция
разделяется на 2n частей, при этом в каждом из частей функция ![]() попеременно принимает положительные и отрицательные значения [9]. Отрицательные части являются регулярными, а положительные части сингулярными областями, а ветви линии
попеременно принимает положительные и отрицательные значения [9]. Отрицательные части являются регулярными, а положительные части сингулярными областями, а ветви линии ![]() пограничными линиями.
пограничными линиями.
Следует отметить, в силу аналитичности функции a(t) существует область содержащий линию ![]() где предел
где предел ![]() не существует.
не существует.
Рассмотрим случай 1.1.
Возьмём линии![]() Часть линии
Часть линии ![]() а часть
а часть ![]() Область, ограниченную линиями
Область, ограниченную линиями ![]() , обозначим
, обозначим ![]() причем будем считать, что эти линии не принадлежат
причем будем считать, что эти линии не принадлежат ![]() .
.
Если ![]() . Для точек
. Для точек ![]() предел
предел ![]() , вообще говоря, не существует.
, вообще говоря, не существует.
Область, ограниченная линиями ![]() , является пограничной областью. Заметим, пограничная область содержит бесчисленное множество пограничных линий. К примеру, в рассматриваемом примере произвольная линия
, является пограничной областью. Заметим, пограничная область содержит бесчисленное множество пограничных линий. К примеру, в рассматриваемом примере произвольная линия ![]() (которая содержится в пограничной области является пограничной линией). При этом пограничная линия
(которая содержится в пограничной области является пограничной линией). При этом пограничная линия ![]() разделяет множество пограничных линий. Целесообразно введение следующего определения
разделяет множество пограничных линий. Целесообразно введение следующего определения
Определение 7. Пограничную линию ![]() , разделяющую множество пограничных линий (пограничную область), назовём главной пограничной линией.
, разделяющую множество пограничных линий (пограничную область), назовём главной пограничной линией.
Пусть рассматривается уравнение
![]() (1)
(1)

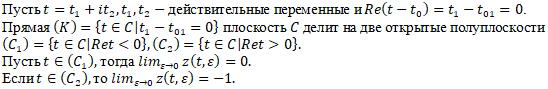
Если ![]() не существует. Согласно принятым определениям,
не существует. Согласно принятым определениям, ![]() -главная пограничная линия;
-главная пограничная линия; ![]() - регулярные области.
- регулярные области.
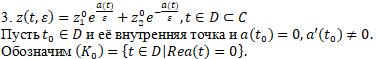
Без ограничения общности будем считать, что линия ![]() область D разделяет на части
область D разделяет на части ![]() (Всегда существует некоторая окрест точки t0 которая линией
(Всегда существует некоторая окрест точки t0 которая линией ![]() разделяется на две части, согласно заданным условиям)[8].
разделяется на две части, согласно заданным условиям)[8].
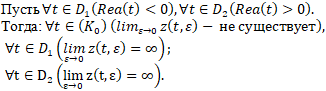
Следовательно ![]() - главная пограничная линия, а
- главная пограничная линия, а ![]() сингулярные области.
сингулярные области.
Различные формы главных пограничных линий
Приведем примеры показывающие различные формы главных пограничных линий.
Пример 1. Пусть задана функция
![]()
![]() - аналитическая функция в некоторой односвязной области t0 внутренняя точка области D.
- аналитическая функция в некоторой односвязной области t0 внутренняя точка области D.
Пусть выполняется условие
При выполнении условия U существует такой гомеоморфизм
![]() достаточно малой окрестности точки t0 на круг, при котором t0 соответствует центру круга.
достаточно малой окрестности точки t0 на круг, при котором t0 соответствует центру круга.
Таким образом, не ограничивая общности, рассмотрим функцию
![]()
Заданную функцию представим в виде
![]()
Полагая![]() рассмотрим следующие функции
рассмотрим следующие функции
![]()
Данные кривые, по совокупности, плоскость C разделяют на несколько частей, причем одна часть, ограниченная частями кривых, является регулярной областью для ![]() , а оставшиеся части сингулярной областью (рис. 1) t2.
, а оставшиеся части сингулярной областью (рис. 1) t2.
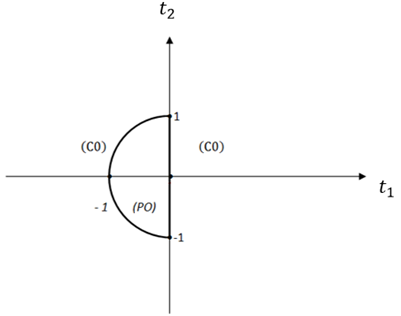
Рис. 1 – Замкнутая главная пограничная линия
Части кривыхПолагая ![]() рассмотрим кривые
рассмотрим кривые
![]()
Кривая ![]() Каждая из ветвей являются полупрямыми, исходящими из данных точек (рис. 2) t2.
Каждая из ветвей являются полупрямыми, исходящими из данных точек (рис. 2) t2.

Рис. 2 – Разветвление кривых
Главная пограничная линия, определяемая рассматриваемыми кривыми, изображена на рис. 3.
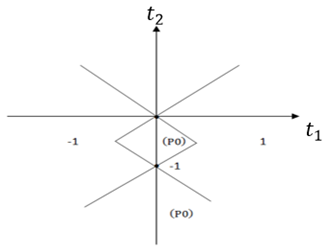
Рис. 3 – Паукообразная главная пограничная линия
Пример 3. Пусть ![]() . Пологая
. Пологая ![]() рассмотрим функцию
рассмотрим функцию ![]() Главная пограничная линия, согласно определению 7, определяется уравнением
Главная пограничная линия, согласно определению 7, определяется уравнением ![]() Отсюда получаем
Отсюда получаем ![]() Данная функция определяет гиперболы, проходящие через точки
Данная функция определяет гиперболы, проходящие через точки ![]() Точка
Точка ![]() является особой для функции
является особой для функции ![]() Таким образом, главная пограничная линия состоит из гиперболы и гиперболы
Таким образом, главная пограничная линия состоит из гиперболы и гиперболы![]() проколотой точкой
проколотой точкой ![]() (рис.4).
(рис.4).
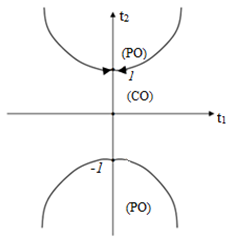
Рис. 4 – Главная пограничная линия, несвязанная с проколотой точкой
Пример 4. ![]() Главная пограничная линия определяется уравнением
Главная пограничная линия определяется уравнением ![]() целое число. Таким образом, прямые
целое число. Таким образом, прямые ![]() являются главными пограничными линиями (рис.5).
являются главными пограничными линиями (рис.5).
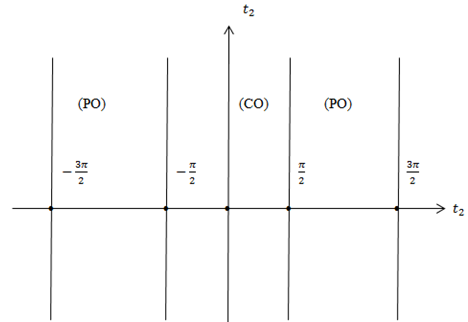
Рис. 5 – Счетное количество главных пограничных линий
Заключение
Рассматриваемые примеры показывают: главные пограничные линии (если они существуют) разделяют рассматриваемые области на регулярные и сингулярные; регулярные и регулярные; сингулярные и сингулярные, а также они имеют различные формы; существуют пограничные области содержащие пограничные линии.
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы / References
- Алыбаев К.С. Метод линий уровня исследования сингулярно возмущенных уравнений при нарушении условия устойчивости / К.С. Алыбаев // Вестник КГНУ. – Серия 3, Выпуск 6. – Бишкек, 2001. – С. 190-200.
- Алыбаев К.С. Метод погранслойных линий построения регулярно и сингулярных областей для линейных сингулярно возмущенных уравнений с аналитическими функциями / К.С. Алыбаев, К.Б. Тампагаров // Естественные и математические науки в современном мире: сб. статей по материалам XLVII международной научно-практической конференции. № 10 (45). Россия, Новосибирск: СиБАК, 2016. - С.59-66.
- Алыбаев К.С. Существование погранслойных линий для линейных сингулярно-возмущенных уравнений с аналитическими функциями / К.С.Алыбаев, К.Б.Тампагаров // Актуальные проблемы, теории управления, топологии и операторных уравнений: Материалы II-й международной конференции, посвященной 20-летию КРСУ и 100-летию профессора Я.В.Быкова. - Бишкек, 2013. - С. 83-88.
- Алыбаев К.С. Явление погранслойных линий и асимптотика решений сингулярно возмущенных линейных обыкновенных дифференциальных уравнений с аналитическими функциями / П.С. Панков, К.С. Алыбаев, М.Р. Нарбаев, К.Б.Тампагаров // Вестник ОшГУ, 2013. - № 1 (специальный выпуск). – C. 227-231.
- Алыбаев К.С. Построение областей притяжения при вырождении сингулярно возмущенных уравнений / К.С. Алыбаев, А.Б. Мурзабаева // Международный научно-исследовательский журнал. № 9 (75). Екатеринбург, 2018. – С. 7-11.
- Мурзабаева А.Б. Построение размеченных множеств применением гармонических функций / А.Б. Мурзабаева // Международный научно-исследовательский журнал. № 9 (75). Екатеринбург, 2018. - С. 32-36.
- Евграфов М.А. Аналитические функции / М.А. Евграфов. – Москва: Наука, 1991. - 448 с.
- Лаврентьев М.А. Методы теории функций комплексного переменного / М.А. Лаврентьев, Б.В. Шабат. – Москва: Наука, 1973. – 739 с.
- Федорюк М.В. Метод перевала / М.В.Федорюк. – Москва: Наука, 1977. - 368 с.
Список литературы на английском языке / References in English
- Alybaev K.S. Metod linij urovnja issledovanija singuljarno vozmushhennyh uravnenij pri narushenii uslovija ustojchivosti [Method of level lines of the study of singularly perturbed equations in violation of the conditions of stability] / K.S. Alybaev // Vestnik KNU. - Series 3, Issue 6. - Bishkek, 2001. - Pp. 190-200. [in Russian]
- Alybaev K.S. Metod pogranslojnyh linij postroenija reguljarno i singuljarnyh oblastej dlja linejnyh singuljarno vozmushhennyh uravnenij s analiticheskimi funkcijami [Method of boundary-layer lines of regular and singular domains construction for linear singularly perturbed equations with analytical functions] / K. S. Alybaev, K. B. Tampagarov // Estestvennye i matematicheskie nauki v sovremennom mire: sb. statej po materialam XLVII mezhdunarodnoj nauchno-prakticheskoj konferencii [Natural and mathematical Sciences in the modern world: collection of articles based on XLVII international scientific-practical conference]. No. 10 (45). Russia, Novosibirsk: Sibak, 2016. - Pp. 59-66. [in Russian]
- Alybaev K.S. Sushhestvovanie pogranslojnyh linij dlja linejnyh singuljarno-vozmushhennyh uravnenij s analiticheskimi funkcijami [The existence of boundary layer lines for linear singularly perturbed equations with analytic function] / K.S.Alybaev, K.B. Tampagarov // Aktual'nye problemy, teorii upravlenija, topologii i operatornyh uravnenij: Materialy II-j mezhdunarodnoj konferencii, posvjashhennoj 20-letiju KRSU i 100-letiju professora Ja.V.Bykova [Actual problems, control theory, topology and operator equations: Materials of the II International Conference anniversary of KRSU and the 100th anniversary of Professor Ya.V. Bykov]. - Bishkek, 2013 .-- P. 83-88. [in Russian]
- Alybaev K.S. Javlenie pogranslojnyh linij i asimptotika reshenij singuljarno vozmushhennyh linejnyh obyknovennyh differencial'nyh uravnenij s analiticheskimi funkcijami [Phenomenon of boundary layer lines and the asymptotics of solutions of singularly perturbed linear ordinary differential equations with analytic functions] / P.S. Pankov, K.S. Alybaev, M.R. Narbaev, K.B. Tampagarov // Vestnik OshGU [Bulletin of Osh State University], 2013. - No. 1 (special issue). - P. 227-231. [in Russian]
- Alybaev K.S. Postroenie oblastej pritjazhenija pri vyrozhdenii singuljarno vozmushhennyh uravnenij / K.S. Alybaev, A.B. Murzabaeva [Construction of regions of attraction at degeneration of singularly perturbed equations] / K. S. Alybaev, A. B. Murzabaeva // Mezhdunarodnyj nauchno-issledovatel'skij zhurnal [International research journal]. No. 9 (75). Ekaterinburg, 2018. - Pp. 7-11. [in Russian]
- Murzabaeva A.B. Postroenie razmechennyh mnozhestv primeneniem garmonicheskih funkcij [Construction of marked sets using harmonic functions] / А.B. Murzabaeva // Mezhdunarodnyj nauchno-issledovatel'skij zhurnal [International research journal]. No. 9 (75). Ekaterinburg, 2018 .-- P. 32-36. [in Russian]
- Evgrafov M. A. Analiticheskie funkcii [Analytical functions] / M. A. Evgrafov. - Moscow: Nauka, 1991. - 448 PP.
- Lavrentiev M. A. Metody teorii funkcij kompleksnogo peremennogo [Methods of the theory of functions of a complex variable] / M. A. Lavrentiev, B. V. Shabat. - Moscow: Nauka, 1973. – 739 p. [in Russian]
- Fedoryuk M. V. Metod perevala [The method of the pass] / M. V. Fedoryuk. Moscow: Nauka, 1977. - 368 p. [in Russian]
