AMPLIFICATION OF NUCLEAR MAGNETOSTATIC OSCILLATIONS IN FERROMAGNETS
УСИЛЕНИЕ ЯДЕРНЫХ МАГНИТОСТАТИЧЕСКИХ КОЛЕБАНИЙ В ФЕРРОМАГНЕТИКАХ
Научная статья
Борич М.А.1, Савченко С.П.2, *
1, 2 Институт физики металлов им. М.Н.Михеева УрО РАН, Екатеринбург, Россия
* Корреспондирующий автор (sergeysavch[at]mail.ru)
АннотацияВ работе рассмотрена задача о связанных электронно-ядерных колебаниях в ферромагнитных образцах сфероидальной формы, имеющих частоты в окрестностях ферромагнитного и ядерного магнитного резонанса. Динамика спиновых волн в указанном диапазоне частот описывается в рамках феноменологической модели, рассматриваемые колебания относятся к магнитостатическими волнам и удовлетворяют магнитостатическим граничным условиям. Спектр колебаний представляет собой дискретный набор собственных мод, частоты некоторых из них получены аналитически. Рассчитан коэффициент усиления магнитного поля, действующего на ядерную подсистему. Исследованы зависимости коэффициента усиления от формы ферромагнетика и собственных частот.
Ключевые слова: электронно-ядерные колебания, магнитный резонанс, ферромагнетики, коэффициент усиления.
AMPLIFICATION OF NUCLEAR MAGNETOSTATIC OSCILLATIONS IN FERROMAGNETS
Research article
Borich M.A.1, Savchenko S.P.2, *
1, 2 M.N. Miheev Institute of Metal Physics of UB RAS, Ekaterinburg, Russia
* Corresponding author (sergeysavch[at]mail.ru)
AbstractThe paper is devoted to the problem of coupled electron-nuclear oscillations in ferromagnets of spheroidal shape with the frequencies in the vicinity of ferromagnetic and nuclear magnetic resonance. In this case, the spin-wave dynamic is described in the framework of the phenomenological model, the considered oscillations are the magnetostatic waves and satisfy the magnetostatic boundary conditions. The spectrum of oscillations represent a discrete set of eigenmodes, and the frequencies of some of them are obtained analytically. The amplification factor of magnetic field acting to the nuclear subsystem is calculated. The dependencies of amplification factor on the shape of a ferromagnetic sample and on the eigenfrequencies are investigated.
Keywords: electron-nuclear oscillations, magnetic resonance, ferromagnets, amplification factor.
IntroductionThe paper is devoted to a detailed analytical investigation of the problem of coupled electron-nuclear magnetostatic oscillations in magnetic materials. The problem of magnetostatic waves propagation in a finite sample was firstly described by L.R.Walker [1]. It was shown that in a sample of spheroidal shape, spectrum of magnetostatic waves splits into a set of discrete modes due to the boundary conditions and this splitting is described by a specific algebraic equations. The problem of coupled electron-nuclear waves in magnetic materials also has been the object of investigation since the 70th of the XXth century [2]. It was shown that some peculiarities of spin wave dynamics occur in the vicinity of nuclear magnetic resonance (NMR) frequencies. Firstly, NMR frequency in magnetic solids is defined mainly by local magnetization, the value of which can differ significantly from external magnetic field. Secondly, resonance transitions of nuclear spins are induced mainly by variable part of electronic magnetization. Small perturbating field produces quite a big oscillations of hyperfine field, which is proportional to the dynamic part of electronic susceptibility at the NMR frequency. This phenomenon is described as the effect of amplification of magnetic field (the order of amplification coefficient usually is about 10 – 103). Thirdly, at low temperatures, the indirect Suhl-Nakamura interaction (SNI) between nuclear spins plays an important role in magnetic dynamics [3]. It effects in substantial broadening of NMR line and in dynamic frequency shift, the value of which depends on the temperature and on the amplitude of nuclear magnetization. The broadening of NMR line and frequency pulling produce specific features in the system dynamics. For example, as it was shown in [4], [5], the relaxation in nuclear subsystem can be produced through relaxation in electronic subsystem. In this case the absolute value of nuclear magnetization remains constant and hence, the relaxation differs from the Bloch type.
Methods
In present article, the homogeneous oscillations of spins in a ferromagnetic sample of spheroidal shape are investigated. Nuclear and electronic spin subsystems are coupled via hyperfine interaction, and the sample’s shape is taken into account through the demagnetization tensor and magnetostatic boundary conditions. The investigated problem includes two important parts: 1) equations of dynamics for the magnetic moments in electronic and nuclear subsystems have to be solved and 2) boundary conditions for a spheroidal sample have to be taken into account. In the framework of the phenomenological description, the energy of the system is given by
![]() (1)
(1)
Here, M and m are the magnetization vectors of electronic and nuclear subsystems, respectively, ![]() describes constant energy term,
describes constant energy term, ![]() is the hyperfine constant,
is the hyperfine constant, ![]() are the external field (H) components,
are the external field (H) components, ![]() is the easy-axis anisotropy field,
is the easy-axis anisotropy field, ![]() are the transverse and longitudinal components of demagnetization tensor of a spheroid – they depend on the relation of spheroid’s semi-axes. The energy of the ferromagnet (1) determines the effective fields
are the transverse and longitudinal components of demagnetization tensor of a spheroid – they depend on the relation of spheroid’s semi-axes. The energy of the ferromagnet (1) determines the effective fields ![]() and
and ![]() , acting to the electronic and nuclear subsystems. These fields are employed in the equations of magnetic moment dynamics for the subsystems:
, acting to the electronic and nuclear subsystems. These fields are employed in the equations of magnetic moment dynamics for the subsystems:
The dissipation is supposed to be negligible here, since it does not have principal effect to the considered problem. To look for solutions for the case of resonance Larmor precession, it is necessary to suppose ![]() . In this case, the linear approximation of equations (2) allows us to obtain the magnetic susceptibility tensor for coupled electron-nuclear oscillations and, thus, solve the first part of the problem. As for the second part, the finiteness and the shape of the sample are taken into account by Maxwell equations in magnetostatic approximation:
. In this case, the linear approximation of equations (2) allows us to obtain the magnetic susceptibility tensor for coupled electron-nuclear oscillations and, thus, solve the first part of the problem. As for the second part, the finiteness and the shape of the sample are taken into account by Maxwell equations in magnetostatic approximation:
Here ψ is the magnetostatic potential, and ![]() designates the magnetic susceptibility tensor, which constitutes the sum of electronic and nuclear susceptibility tensors. Equations (3) can be written in further form for regions outside and inside the sample, respectively:
designates the magnetic susceptibility tensor, which constitutes the sum of electronic and nuclear susceptibility tensors. Equations (3) can be written in further form for regions outside and inside the sample, respectively:
In accordance with magnetostatic boundary conditions, the continuousness of tangential component of magnetic field leads to the continuousness of ψ. The finite solutions of Eq. (5) satisfying this condition are expressed in terms of the associated Legendre polynomials ![]() of the first and second kinds. Thus, the solutions are numerated by the pair of indexes (n,m). The continuousness of normal component of magnetic induction leads to the algebraic equation with respect to ω:
of the first and second kinds. Thus, the solutions are numerated by the pair of indexes (n,m). The continuousness of normal component of magnetic induction leads to the algebraic equation with respect to ω:
![]() (6)
(6)
Where a, b are the semi-axes of ellipsoid of revolution, ![]() is the value that is determined by the frequency,
is the value that is determined by the frequency, ![]() , and are the permeability tensor components. The solutions of characteristic equation (6) represent the resonance frequencies for coupled electron-nuclear oscillations in external magnetic field.
, and are the permeability tensor components. The solutions of characteristic equation (6) represent the resonance frequencies for coupled electron-nuclear oscillations in external magnetic field.
Results
The solutions of equation (6) can be analytically obtained for m=n and m=n − 1 cases. The general properties of the problem can be demonstrated with these analytically-described solutions of the equation. For these solutions, the eigenfrequencies ω are given by
![]() (7)
(7)
and are determined by the shape of the sample and the indexes (n,m). Here “+” and “−” signs correspond to nuclear and electronic solutions, respectively. Other designations are as follows:
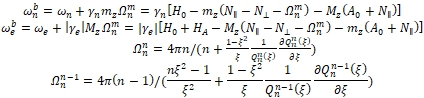
The comparison of (7) and (8) shows that the boundary conditions renormalize demagnetization factor (![]() ), i.e. the frequency-dependent demagnetization factors
), i.e. the frequency-dependent demagnetization factors ![]() can be introduced. Note that (1,1) oscillation corresponds to the homogeneous ferromagnetic resonance (FMR) and the equality
can be introduced. Note that (1,1) oscillation corresponds to the homogeneous ferromagnetic resonance (FMR) and the equality ![]() is fulfilled for any shape of the ellipsoid. Thus, the shape dependence of the FMR frequency can be represented via one of three parameters:
is fulfilled for any shape of the ellipsoid. Thus, the shape dependence of the FMR frequency can be represented via one of three parameters: ![]() .
.
As it was mentioned, the behavior of nuclear spins in a ferromagnetic material is determined not just by an external field, but also by the effective field that appears due to exchange and hyperfine interactions. The effective field may exceed the external field by 2 or 3 orders of magnitude. The coefficient η designating the relation between the effective field acting to the nuclear subsystem and external perturbing field (Hnucl~ηh) is called the amplification factor [2], and it is important to consider the shape dependence of this most important parameter of oscillations. The amplification factor in our problem is given by
![]() (9)
(9)
We estimated the value of η for MnFe2O4 compound, the material parameters of which are known: A0 has the order 103, Ha and Mz have the order 103 Oe, mzA0~101 Oe [6]. Eq. (9) coincides with “non-magnetic” amplification coefficient presented in [2]. This coefficient is strongly dependent on the shape and the type of oscillations, it has the order of magnitude ~102. The calculation of η shows that the more oblate our sample is, the bigger the amplification is. Amplification coefficient for (n,n-1)-oscillations is bigger than that for (n,n). Additionally, the bigger the indexes are, the smaller the amplification is. This statement is correct both for (n,n)- and (n,n-1)-series of eigenfrequencies. Some values of amplification coefficient for MnFe2O4 are presented in Table 1.
Table 1 – Amplification coefficients for various shapes and different indexes n, m
| H0=1500 Oe | a/b=0.5 (oblong spheroid) | a/b=1 (sphere) | a/b=2 (oblate spheroid) |
| 87 | 130 | 342 | |
| 83 | 116 | 265 | |
| 82 | 113 | 237 | |
| 96 | 165 | 807 | |
| 88 | 141 | 511 |
The presented results were obtained by employing the dynamic equations without the dissipation terms. Taking them into account leads to a more complicated representation of permeability tensor, but does not change significantly the characteristic equation, and it still possesses analytical solutions for m=n and m=n − 1 cases. The shift of eigenfrequencies due to the dissipation has the second order of magnitude relative to dissipation parameters. The change of the amplification factor due to the dissipation is also second-order effect therefore. It allows us to argue that (at least small) dissipation does not change our principal results.
Conclusion
In this paper, some new features in the problem of coupled electron-nuclear oscillations in ferromagnets of spheroidal shape have been obtained. The main results of this paper are compiled as follows:
- The eigenmodes of coupled electron-nuclear oscillations in ferromagnets of spheroidal shape represent a discrete set. They are expressed through the associated Legendre polynomials and numerated by a pair of indexes (n,m).
- For eigenfrequencies with m=n and m=n-1, it was defined that the boundary conditions due to the finiteness of the sample lead to the renormalization of transverse component of demagnetization tensor as follows:
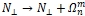 . Other kinds of magnetostatic oscillations renormalize
. Other kinds of magnetostatic oscillations renormalize 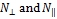 in a more complicated way.
in a more complicated way. - The effective field acting to the nuclear subsystem from the electronic one significantly depends on the shape of the sample and on the eigenfrequency, i.e. (1) amplification factor depends on the the shape of the sample, and (2) different eigenmodes have the different amplification factors, and the difference may be significant.
| Финансирование Работа выполнена в рамках государственного задания МИНОБРНАУКИ России (тема «Функция», № АААА-А19-119012990095-0) и проекта ИФМ УрО РАН № 18-10-2-37. | Funding The research was carried out within the state assignment of Ministry of Science and Higher Education of the Russian Federation (theme “Function” No. АААА-А19-119012990095-0) and UB RAS project No.18-10-2-37. |
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы / References
- Walker L.R. Magnetostatic Modes in Ferromagnetic Resonance / L.R.Walker // Physical Review. – 1957. – V.105. – №1.– P. 390–399.
- Turov E. Nuclear Magnetic Resonance in Ferro- and Antiferromagnets / Turov E., Petrov M. – New York, Halstead Press, 1972 .– 206 p.
- De Gennes P.G. Nuclear Magnetic Resonance Modes in Magnetic Material. I Theory / de Gennes P.G., Pinkus P.A., Hartman-Boutron F. and others // Physical Review. – 1963. – V.129. – №3.– P.1105-1115.
- Borich M. Nuclear magnetic relaxation induced by the relaxation of electron spins / Borich M., Bunkov Y., Kurkin M., Tankeyev A. // JETP Letters . – 2017. – V.105. – № 1.– P.23-27.
- Abdurakhimov L. Nonlinear NMR and magnon BEC in antiferromagnetic materials with coupled electron and nuclear spin precession / Abdurakhimov L., Borich M., Bunkov Y. and others // Physical Review B .– 2018 .– V.97 .– 024425 .– P. 1-11.
- Blocker T.G. Coupled Electron-Nuclear Magnetostatic Modes in Magnetic Materials / T.G. Blocker, III // Physical Review. – 1967. – V.154. – № 2.– P. 446–447.
- Nakamura T. Indirect Coupling of Nuclear Spins in Antiferromagnet with Particular Reference to MnF2 at Very Low Temperatures / T.Nakamura // Progress in Theoretical Physics. –1957. – V.20. –№4. –P.542-552
- Fletcher P.C. Ferrimagnetic Resonance Modes in Spheres / P.C.Fletcher and R.O.Bell // Journal of applied physics. –1957. –V.30. –№ 5. –P.687-698
- G.Heeger, Mn55 nuclear magnetic resonance in manganese ferrite / A. J. Heeger, S. K. Ghosh, T. G. Blocker, III // Journal of applied physics. –1963. –V.34. –№ 4. –P.1034-1035
- King A.R. Nuclear Magnons and nuclear magnetostatic modes in MnF2 / A.R.King, V.Jaccarino, S.M.Rezende // Physical Review Letters.–1976. –V.37. –№9 . –P.533-536
