IMPLEMENTATION OF THE PRINCIPLE OF HYPOTHENNITY IN TRAINING MATHEMATICS OF PEOPLE WITH DISABILITIES OF HEALTH IN THE HIGHER EDUCATIONAL INSTITUTION

Виноградова Ю. А.¹, Иванова О. К.², Яновская Е. А.³

¹ORCID: 0000-0003-3523-5371, ²ORCID: 0000-0003-2524-6325, кандидат физико-математических наук, ³ORCID: 0000-0002-0855-7300, кандидат технических наук, ФГБОУ ВО МГТУ «СТАНКИН»

РЕАЛИЗАЦИЯ ПРИНЦИПА НАГЛЯДНОСТИ ПРИ ОБУЧЕНИИ МАТЕМАТИКЕ ЛЮДЕЙ С ОГРАНИЧЕННЫМИ ВОЗМОЖНОСТЯМИ ЗДОРОВЬЯ В ВЫСШЕМ УЧЕБНОМ ЗАВЕДЕНИИ

Аннотация

Создание безбарьерной среды для людей с ограниченными возможностями в современном мире приобретает весьма большое значение. Необходимо адаптировать людей, сталкивающихся с серьезными проблемами по здоровью к реалиям современного мира. Помогать получать профессиональные знания, в том числе в технических и технологических университетах. Подобные программы имеют широкую гуманистическую направленность: позволяют людям с ограниченными возможностями по здоровью жить полноценной жизнью, обеспечивая себя и свои семьи достойной заработной платой, тем самым создавая устойчивый фундамент для развития современного гражданского общества в России. В связи с необходимостью развивать новые методики образования для инвалидов в России активно развивается законодательная и правовая база для создания всех условий получения образования детьми с ограниченными возможностями по здоровью и детьми-инвалидами.

В данной работе показано как можно применить принцип наглядности при обучении учащихся с ограниченными возможностями здоровья и дать им возможность осознать и понять достаточно трудный для восприятия материал. Для примера, в рамках отдельно взятой математической темы с большим количеством труднодоступных абстрактных понятий, рассмотрены различные способы введения понятия предела последовательности в целях реализации принципа наглядности при обучении людей с ограниченными возможностями здоровья.

Благодаря применению принципа наглядности у студентов с ограниченными возможностями по здоровью, независимо от типов нозологических групп инвалидности, возникает интерес к обучению и дальнейшей реализации своих возможностей, что существенно повышает качество получаемого образования. Специалисты, получившие высшее образование благодаря таким методам могут быть успешно интегрированы для работы в научно-производственных объединениях, заниматься научной работой и педагогической практикой, в том числе в вузах.

Ключевые слова: высшее образование, доступная среда, люди с ограниченными возможностями здоровья, математика, предел последовательности, принцип наглядности.

Vinogradova Yu.A.¹, Ivanova O.K.², Yanovskaya E.A.³

¹ORCID: 0000-0003-3523-5371, ²ORCID: 0000-0003-2524-6325 PhD in Physics and Mathematics, ³ORCID: 0000-0002-0855-7300 PhD in Engineering, FSBEI of HE MSTU "STANKIN"

IMPLEMENTATION OF THE PRINCIPLE OF HYPOTHENNITY IN TRAINING MATHEMATICS OF PEOPLE WITH DISABILITIES OF HEALTH IN THE HIGHER EDUCATIONAL INSTITUTION

Abstract

Creating a barrier-free environment for people with disabilities in the modern world is very important. It is necessary to adapt people facing serious health problems to the realities of the modern world, to help them to obtain professional knowledge, including in technical and technological universities. Such programs have a broad humanistic orientation: they allow people with limited health opportunities to live a full life, providing themselves and their families with decent wages, thereby creating a stable foundation for the development of modern civil society in Russia. In connection with the need to develop new methods of education for the disabled in Russia, the legislative and legal framework for the creation of all conditions for the education of children with health disabilities and disabled children is actively developing.

In this paper it is shown how to apply the principle of visibility in teaching students with disabilities and give them the opportunity to realize and understand a material that is difficult to perceive. For example, within the framework of a single mathematical topic with a large number of abstract concepts difficult to access, various ways of introducing the concept of a limit of sequence are considered in order to realize the principle of visibility in the teaching of people with disabilities.

Because of the application of the principle of visibility in students with disabilities in health, regardless of the types of nosological groups of disability, there is an interest in learning and furthering their opportunities, which significantly improves the quality of the education. Specialists who received higher education due to such methods can be successfully integrated to work in scientific and industrial associations, engage in scientific work and pedagogical practice, including in universities.

Keywords: higher education, accessible environment, people with disabilities, mathematics, limit of consistency, principle of visibility.

Высшее образование в современном мире является неотъемлемой частью жизни. Молодежь стремится получить высшее техническое или технологическое образование. Люди с ограниченными возможностями здоровья – не исключение. Вузы Российской Федерации, и МГТУ «СТАНКИН», в частности, ставят перед собой задачу организовать удобную образовательную среду для обучения таких людей.

К сожалению, число людей, имеющих ограниченные возможности по здоровью, велико. В связи с этим перед мировым сообществом возникает большая проблема по адаптации этих людей к условиям современной жизни, их лечению, образованию и их внедрению в производительный труд.

В последние десятилетия кардинально поменялся взгляд мирового сообщества, в том числе и в Российской Федерации, на проблемы людей с ограниченными возможностями по здоровью. Развитие гражданского общества в России создало новые возможности для проведения социальных реформ, в том числе для людей с ограниченными возможностями по здоровью.

Изучение источников по проблеме показывает, что это не только российское явление, но и общеевропейская и даже общемировая тенденция. Движение за права людей с ограниченными возможностями поддерживается программами ООН [1].

Создание благоприятных условий для получения людьми с инвалидностью технического и технологического образования в вузах – первоочередная задача университетов России. Для этого необходимо развитие безбарьерной среды не только физически, но и в гуманитарном плане. Такая среда необходима для реализации всех возможностей талантливых детей при получении сложных профессий, востребованных на современном рынке труда. Впоследствии, полученное образование позволяет людям с инвалидностью и ограниченными возможностями по здоровью занять достойное место в современном мире и полностью быть интегрированными в современных условиях.

Конституция и законы России создают правовую базу и дают гарантию для реализации права на получение качественного образования в ведущих высших учебных заведениях России для этой категории граждан [2], [3].

Если обратить внимание на исследования доступности высшего образования людей с ограниченными возможностями здоровья, можно увидеть, что многие проблемы обусловлены неприспособленностью среды вуза, а также низким качеством подготовки в средних, средних специальных учебных заведениях и колледжах [4, С. 48]. Эти факторы обуславливают возникновение некоторых дополнительных трудностей при получении технического и технологического образования. В решении данных вопросов можно широко применять так называемое дистанционное образование [5]. Основная цель, которая реализуется с помощью дистанционного образования – это создание условий для людей с ограниченными возможностями по здоровью для обучения непосредственно по месту проживания, предоставление возможности освоения образовательных программ высшего образования. Процесс получения образования с использованием дистанционных методов обучения может осуществляться образовательным учреждением в виде различных форм: очной, очно-заочной, заочной и т.д. [6].

 В данной работе мы не будем обсуждать особенности архитектуры зданий, дверных проемов, специального оборудования для перемещения людей с ограниченными возможностями здоровья. Обучение в техническом университете возможно для людей с различными типами нозологических групп инвалидности: с нарушениями интеллекта (нарушения речи, внимания, общения вследствие перенесенных заболеваний, в том числе онкологических), поражениями опорно-двигательного аппарата (церебральное, спинальное и ампутационное). Покажем на примере преподавания математики (отдельно взятой темы), реализацию принципа наглядности в обучении, который поможет учащимся с ограниченными возможностями здоровья осознать и понять достаточно трудный для восприятия материал.

Математика, как известно, является наиболее сложным предметом для учащихся. Это связано с обильным количеством труднодоступных абстрактных понятий.

Еще Я.А. Коменский сформулировал “золотое правило дидактики”: “Все, что только можно, предоставлять для восприятия чувствами, а именно: видимое – для восприятия зрения, слышимое – слухом, запахи – обонянием, что можно вкусить – вкусом, доступное осязанию – путем осязания. Если какие-либо предметы сразу можно воспринять несколькими чувствами, пусть они сразу схватываются несколькими чувствами” [7, С. 38]. Наглядность в понимании Коменского связана с восприятием предметов (явлений) органами чувств.

Обратимся к определению понятия наглядности [8, С. 215]:

«Наглядность. Термин используется в двух значениях:

1) как опора в процессе обучения на дидактический принцип наглядности, согласно которому обучение строится на конкретных образах, непосредственно воспринимаемых учащимися;

2) как использование на занятиях специальных средств обучения, опирающихся на принцип наглядности (аудиовизуальные средства обучения, технические средства обучения)».

Приведем пример введения понятия предела последовательности. Заметим, что это понятие является одним из основополагающих в математике, и одновременно с этим, наиболее трудно воспринимающимся не только студентами с особенностями здоровья, но и обычными студентами.

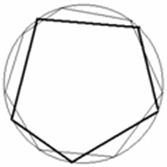
Рис. 1 –  Наглядное формирование понятия предела при выводе формулы длины окружности

 

Если обратиться к истории введения понятия предела последовательности, увидим, что зачатки данного понятия формируются при выводе формул вычисления длины окружности и площади круга (рис. 1).

Вывод данных формул предшествовал обучению теории пределов. Обратимся к изданию А.П. Киселева «Элементарная геометрия»  [9, С. 75]. На странице 75, перед введением понятия предела, демонстрируется движение в геометрии: «Пусть к окружности О проведены через точку А касательная АТ и какая-нибудь секущая АМ. Станем вращать эту секущую вокруг точки А так, чтобы  другая точка пересечения В все ближе придвигалась к А. … » (рис.2).

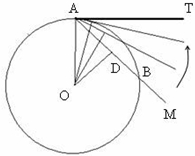
Рис. 2 –  Вращение секущей вокруг точки А

 

Далее рассматривается угол МАТ, который связан с точкой В, движущейся к точке А по окружности и который может быть «сделан как угодно мал». Этот процесс «выражают иными словами так: касательная есть предельное положение, к которому стремится секущая, проведенная через точку касания, когда вторая точка пересечения неограниченно приближается к точке касания» [9, С. 76]. Но далее на странице 158 в разделе «Определение длины окружности и ее частей», в главе первой «Основные свойства пределов», используя геометрически образные различие между понятиями постоянной и переменной величинами, возвращая учащегося к приведенному на стр. 76 понятию движения и демонстрации «сколь угодно малого угла» еще говорится о приближении переменной точки В к постоянной (фиксированной) точке А. И дается определение: «Пределом переменной величины называется такая постоянная величина, к которой переменная приближается так, что разность между ними стремится к нулю» [9, С. 159].

Если в современном обучении математике студентов с ограниченными возможностями здоровья мы будем обращаться к геометрическим образам,

прежде, чем переходить к языку «ε−δ», мы покажем, что предельный переход − это процесс, при этом совершенно ощутимый, изображаемый (наглядный), и столь трудное словосочетание «сколь угодно малый» окажется наглядно представленным.

В современном курсе математики общеобразовательной школы, независимо от принятого школой учебника, некоторые понятия вводятся через пределы.  Говоря ученику, что площадь круга есть такой-то предел, − но определение предела в школе либо не дается вообще, либо дается очень кратко (учебники Алимова Ш. А., Колмогорова А. Н.) − школьная программа приводит к тому, что что-то не договаривается, и некоторые доказательства будут когда-то даны [10].

В учебнике алгебры [11, С. 108] А. П. Киселева понятие предела дается в дополнительном разделе:

«Возьмем сумму первых n членов такой бесконечно убывающей геометрической прогрессии:

Сумма эта при неограниченном увеличении числа членов увеличивается, приближаясь к постоянному числу 2 так, что разность

при достаточном увеличении числа слагаемых делается меньше любого данного положительного числа (например, меньше 0,000001) и при дальнейшем увеличении числа слагаемых остается всегда меньше этого числа.

При этих условиях мы говорим, что сумма

если число слагаемых в ней увеличивается неограниченно, имеет предел 2.

После этих примеров будет понятно следующее определение предела:

Если переменная величина х при своем изменении приближается к постоянной величине а так, что абсолютная величина разности а–х (или х–а) может быть сделана и в дальнейшем остается меньше любого положительного числа, то эта постоянная величина а называется пределом переменной х» [11, С. 112]. Подведение к понятию предела в данном случае сопровождается примерами, а само определение дано не через «ε−δ», что, возможно, облегчает восприятие и понимание.

Далее приведем определение, которое дается в учебнике Д. К. Фаддеева и И. С. Соминского [12, С. 156].

 «Последовательность

общий член которой , изображена на рисунке 3.  

Рис. 3 –  Графическое изображение последовательности 

 

Наблюдая за расположением точек последовательности, легко заметить, что они все ближе и ближе подходят к нулю, накапливаются около нуля.

Пусть ε любое положительное число. Возьмем на числовой оси отрезок длиной 2ε с центром в точке О.

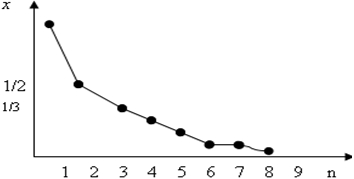
Рис. 4 –  Графическое изображение последовательности 

Найдется такой номер N, что всякая точка последовательности с номером, большим N, будет находиться внутри этого отрезка.

Число N, конечно, зависит от ε. Чем меньше ε, тем, вообще, больше будет N.

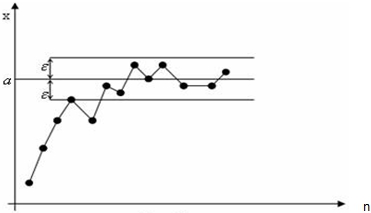
Рис. 5 – Графическое изображение последовательности 

Определение 1: Число а называется пределом последовательности, если для каждого положительного числа ε, сколь бы мало оно не было, существует такой номер N, что все точки последовательности, у которых номер больше N, будут находиться от а на расстоянии меньшем, чем ε.

Для того чтобы точка b находилась на числовой оси на расстоянии, меньшем ε от точки а, необходимо и достаточно, чтобы  .

На основании этого определение предела можно сформулировать так:

Определение 2: Число а называется пределом последовательности

если для каждого положительного числа ε, сколь бы мало оно не было, существует такой номер N, что все значения a_n, у которых номер n>N, удовлетворяют неравенству

Это же определение можно сформулировать и так: Определение 3: Число а называется пределом последовательности

если члены последовательности, начиная с некоторого места, отличаются от а сколь угодно мало.» [11, С. 111].

В данном случае автор постепенно с помощью наглядных графических представлений приводит к определению. Поскольку переход на язык «ε–δ» труден для восприятия и требует перестройки мышления, возможно, целесообразней было бы сначала давать определение 3, а затем переходить к определению 1 и 2.

Далее рассмотрим задачи, связанные с определением предела и само определение предела, предлагаемые А. А. Кирилловым [13, С. 76], которые, на наш взгляд, являются наиболее наглядными.

«Рассмотрим график последовательности  (рис. 4).

Мы видим, что этот график неограниченно приближается к оси абсцисс,  стремится к ней.

Слова «неограниченно приближается» и «стремится» понятны каждому, пока речь идет о наглядных свойствах графика. Однако, чтобы использовать их в математических рассуждениях и вычислениях, такого понимания недостаточно. Мы должны точно сформулировать, что означают эти выражения на языке чисел. Это приводит нас к одному из самых важных понятий, используемых в математике, – к понятию предела.

Дадим сначала точное определение предела в той форме, в какой оно обычно встречается в учебниках.

Число а называется пределом последовательности  если для любого положительного числа ε (греческая буква «эпсилон») найдется такое число k, что для всех номеров n, больших k, выполняется неравенство

Записывают этот факт так: 

Сделаем теперь несколько замечаний по поводу определения предела.

Рассмотрим график последовательности   (рис.5).

Какое свойство этого графика выражается равенством

Проведем горизонтальную прямую x = a и построим полоску ширины 2ε, окружающую эту прямую. Неравенство   означает, что точка

 находится внутри построенной полоски. Таким образом, если последовательность  стремится к а, то почти весь график последовательности лежит внутри указанной полоски.

Так как в определении предела число ε может быть любым сколь угодно малым, описанное свойство графика сохраняется для любой сколь угодно малой полоски. Итак, определение предела может быть пересказано следующим образом.

Число а называется пределом последовательности , если почти весь график этой последовательности лежит внутри сколь угодно узкой полоски, окружающей прямую x = a.

Наглядное представление о пределе можно получить, если предположить, что члены последовательности – какие-то физические величины, и мы можем измерить их только с определенной точностью, которую допускают наши приборы.

Обозначим через ε наименьшую величину, различаемую прибором. Неравенство  означает, что мы не сможем отличить x_n  от а.

Таким образом, условие  означает, что при любой точности измерения последовательность , начиная с некоторого места, не отличается от постоянной последовательности а, а, а, ….

Еще раз укажем, что данное определение предела последовательности сформулировано просто, наглядно, с геометрическими и физическими образами, а это для учащегося с ограниченными возможностями здоровья очень важно.

В результате рассмотренных методов введения понятия предела реализуется один из важнейших принципов обучения – принцип наглядности, который позволяет студенту воспринять и понять одно из сложнейших понятий математического анализа – предел последовательности.

В итоге, учитывая особенности обучающихся (независимо от типов нозологических групп учащихся, при которых возможно получение высшего образования) при работе с формой, с картинкой, с интеллектуальным образом, принцип наглядности в определении предела последовательности помогает перейти к сущности этого понятия.

Благодаря применению принципа наглядности у студентов с ограниченными возможностями по здоровью, возникает интерес к обучению и дальнейшей реализации своих возможностей, что существенно повышает качество получаемого образования [14, С. 213]. Специалисты, получившие высшее образование благодаря таким методам могут быть успешно интегрированы для работы в научно-производственных объединениях, заниматься научной работой и педагогической практикой, в том числе в вузах.

Список литературы / References

1. Конвенция о правах инвалидов. 13 дек. 2006 г. [Электронный ресурс]. URL: www.un.org/ru/documents/decl_conv/conventions/disability.shtml  (дата обращения 20.05.2017)
2. Федеральный Закон «О высшем и послевузовском профессиональном образовании» Федеральный закон от 29.12.2012 N 273-ФЗ (ред. от 29.07.2017) "Об образовании в Российской Федерации". Статья 79. URL:  www.consultant.ru/document/cons_doc_LAW_140174/  (дата обращения 25.06.2017)
3. Федеральный Закон «О социальной защите инвалидов в Российской Федерации» (Федеральный закон от 24.11.1995 N 181-ФЗ (ред. от 01.06.2017) "О социальной защите инвалидов в Российской Федерации". Статья 19. URL:   http://www.consultant.ru/document/cons_doc_LAW_8559/ (дата обращения 23.06.2017)
4. Романов П. В. Проблема доступности высшего образования для инвалидов / П. В. Романов, Е. Р. Ярская-Смирнова // Социологические исследования. – 2005. – № 10. – С. 48-56.
5. Приказ Минобразования РФ № 4452 от 18.12.02 «Об утверждении Методики применения дистанционных образовательных технологий (дистанционного образования) в образовательных учреждениях высшего, среднего и дополнительного профессионального образования РФ». (Приказ Минобразования РФ от 18.12.2002 N 4452 "Об утверждении Методики применения дистанционных образовательных технологий (дистанционного обучения) в образовательных учреждениях высшего, среднего и дополнительного профессионального образования Российской Федерации" (Зарегистрировано в Минюсте РФ 24.12.2002 N 4071). – URL:   http://www.consultant.ru/document/cons_doc_LAW_40163/ (дата обращения 13.07.2017)
6. Приказ Минобразования РФ от 14.10.1997 N 2033 "Об утверждении Положения об экстернате в государственных, муниципальных высших учебных заведениях Российской Федерации" (Зарегистрировано в Минюсте РФ 30.10.1997 N 1403). URL: http://www.consultant.ru/document/cons_doc_LAW_16638/ (дата обращения 24.06.2017)
7. Коменский Я. А. Великая дидактика / Я. А. Коменский // Избр. пед. соч. – М., 1982. – Т.1. – 271 с.
8. Азимов Э. Л. Словарь методических терминов / Э. Л. Азимов, А. И. Щукин. – СПб.: Издательство «Златоуст». – 1999. – 472 с.
9. Киселев А.П. Элементарная геометрия / А. П. Киселев. – М.: Издание книжного магазина В. В. Думнова. – 1892. – 307 с.
10. Виноградова Ю. А. О причинах методических сложностей перехода от «конечного» к «бесконечному» в курсе математического анализа в вузе / Ю. А. Виноградова, В. К. Жаров // Сборник научных трудов «Фундаментальные физико-математические проблемы и моделирование технико-технологических систем», – М.: Янус-К, ИЦ МГТУ «Станкин». – 2006. № 9. – С. 167.
11. Киселев А. П. Алгебра / А. П. Киселев // Учебник для 9-10 классов средней школы. – М.: Издательство «Просвещение», 1965. – 232 с.
12. Фаддеев Д. К. Алгебра / Д. К. Фаддеев, И. С. Соминский. – Ленинград: Издательство «Учпедиздат», 1954. – Ч. 2. –  288 с.
13. Кириллов А. А.. Пределы / А. А. Кириллов // М.: Издательство «Наука», 1973. – 97 с.
14. Белякова А.А. Философско-педагогическая рефлексия принципа наглядности / А. А. Белякова, Л. А. Буровкина // Вестник ТГТУ. – 2010. – Т. 16. ­ №1. –С. 212 – 217.

Список литературы на английском языке / References in English

1. Konvencija o pravah invalidov [Convention on the Rights of Persons with Disabilities]. 13 dec. 2006. [Electronic resource] URL:www.un.org/ru/documents/decl_conv/conventions/disability.shtml (accessed 20.05.2017) [in Russian]
2. Federal'nyj Zakon «O vysshem i poslevuzovskom professional'nom obrazovanii» Federal'nyj zakon ot 29.12.2012 N 273-FZ [The Federal Law "On Higher and Post-Graduate Professional Education" Federal Law No. 273-FZ of December 29, 2012] (edited from July 29, 2017) "Ob obrazovanii v Rossijskoj Federacii". Stat'ja 79 ["On Education in the Russian Federation". Article 79].URL: www.consultant.ru/document/cons_doc_LAW_140174/ (accessed 25.06.2017) [in Russian]
3. Federal'nyj Zakon «O social'noj zashhite invalidov v Rossijskoj Federacii» (Federal'nyj zakon ot 24.11.1995 N 181-FZ [The Federal Law "On the Social Protection of Persons with Disabilities in the Russian Federation" (Federal Law No. 181-FZ of November 24, 1995)] (edited from June 01, 2017) "O social'noj zashhite invalidov v Rossijskoj Federacii". Stat'ja 19 ["About the Social Protection of Persons with Disabilities in the Russian Federation". Article 19]. URL: http://www.consultant.ru/document/cons_doc_LAW_8559/ (accessed 23.06.2017) [in Russian]
4. Romanov P. V. Problema dostupnosti vysshego obrazovanija dlja invalidov [The problem of accessibility of higher education for the disabled] / P. V. Romanov, E. R. Jarskaja-Smirnova // Sociologicheskie issledovanija [Sociological research]. – 2005. – № 10. – P. 48–56. [in Russian]
5. Prikaz Minobrazovanija RF № 4452 ot 18.12.02 «Ob utverzhdenii Metodiki primenenija distancionnyh obrazovatel'nyh tehnologij (distancionnogo obrazovanija) v obrazovatel'nyh uchrezhdenijah vysshego, srednego i dopolnitel'nogo professional'nogo obrazovanija RF». [Order of the Ministry of Education of the Russian Federation No. 4452 dated December 18, 2002 "On Approving the Methodology for Using Remote Educational Technologies (Distance Education) in Higher, Secondary and Additional Vocational Education Institutions in the Russian Federation".] (Registered in the Ministry of Justice of the Russian Federation on December 24, 2002 No. 4071). – URL: http://www.consultant.ru/document/cons_doc_LAW_40163/ (accessed 13.07.2017) [in Russian]
6. Prikaz Minobrazovanija RF ot 14.10.1997 N 2033 "Ob utverzhdenii Polozhenija ob jeksternate v gosudarstvennyh, municipal'nyh vysshih uchebnyh zavedenijah Rossijskoj Federacii" [Order of the Ministry of Education of the Russian Federation of 14.10.1997 N 2033 "On approval of the Regulation on external studies in state, municipal higher education institutions of the Russian Federation"] (Registered in the Ministry of Justice of the Russian Federation on 30.10.1997 N 1403). URL: http://www.consultant.ru/document/cons_doc_LAW_16638/ (accessed 24.06.2017) [in Russian]
7. Komenskij Ja. A. Velikaja didaktika [Great Didactics] / Ja. A. Komenskij // Izbr. ped. Soch [Selected Pedagogical Compositions]. – M., 1982. – T.1. – 271 p. [in Russian]
8. Azimov Je. L. Slovar' metodicheskih terminov [Dictionary of Methodological Terms] / Je. L. Azimov, A. I. Shhukin. – SPb.: Izdatel'stvo «Zlatoust». – 1999. – 472 p. [in Russian]
9. Kiselev A.P. Jelementarnaja geometrija [Elementary geometry] / A. P. Kiselev. – M.: Izdanie knizhnogo magazina V. V. Dumnova. – 1892. – 307 p. [in Russian]
10. Vinogradova Ju. A. O prichinah metodicheskih slozhnostej perehoda ot «konechnogo» k «beskonechnomu» v kurse matematicheskogo analiza v vuze [About the reasons for the methodological difficulties of the transition from "finite" to "infinite" in the course of mathematical analysis in the university] / Ju. A. Vinogradova, V. K. Zharov // Sbornik nauchnyh trudov «Fundamental'nye fiziko-matematicheskie problemy i modelirovanie tehniko-tehnologicheskih sistem» [Collection of scientific papers "Fundamental physics and mathematics problems and Modeling of technical and technological systems "], – M.: Janus-K, IC MGTU «Stankin». – 2006. № 9. – P. 167. [in Russian]
11. Kiselev A. P. Algebra [Algebra] / A. P. Kiselev // Uchebnik dlja 9-10 klassov srednej shkoly [Textbook for 9-10 grades of secondary school]. – M.: Izdatel'stvo «Prosveshhenie», 1965. – 232 p. [in Russian]
12. Faddeev D. K. Algebra [Algebra] / D. K. Faddeev, I. S. Sominskij. – Leningrad: Izdatel'stvo «Uchpedizdat», 1954. – Part. 2. – 288 p. [in Russian]
13. Kirillov A. A. Predely [Limits] / A.A. Kirillov. – M.: Izdatel'stvo «Nauka», 1973. – 97 p. [in Russian]
14. Beljakova A.A. Filosofsko-pedagogicheskaja refleksija principa nagljadnosti [Philosophical and pedagogical reflexion of the principle of visibility] / A. A. Beljakova, L. A. Burovkina // Vestnik TGTU [Bulletin of TSTU]. – 2010. – T. 16, №1. – P. 212–217. [in Russian]