ON DIFFUSION IN LATTICE GAS FOR LARGE CONCENTRATION GRADIENTS
О ДИФФУЗИИ В РЕШЕТОЧНОМ ГАЗЕ ПРИ БОЛЬШИХ ГРАДИЕНТАХ КОНЦЕНТРАЦИЙ
Научная статья
Трощиев Ю.В. *
ORCID: 0000-0001-6805-7001,
Московский Государствнный Университет, Москва, Россия
* Корреспондирующий автор (yuvt[at]yandex.ru)
АннотацияВ работе выводятся из уравнений химической кинетики удобные для исследования выражения для потоков и коэффициентов диффузии в неидеальном решеточном газе. Коэффициенты являются линейными операторами, зависящими от концентраций и их градиентов. Показано, что направление потока может составлять любые углы с направлением градиента.
Ключевые слова: решеточный газ, коэффициенты диффузии, уравнения химической кинетики.
ON DIFFUSION IN LATTICE GAS FOR LARGE CONCENTRATION GRADIENTS
Research article
Troshchiev Yu.V. *
ORCID: 0000-0001-6805-7001,
Moscow State University, Moscow, Russia
* Corresponding author (yuvt[at]yandex.ru)
AbstractThe article derives expressions for flows and diffusion coefficients in an imperfect lattice gas from equations of chemical kinetics convenient for study. Coefficients are linear operators depending on concentrations and their gradients. It is shown that the flow direction can build any angle with the direction of the gradient.
Keywords: lattice gas, diffusion coefficients, chemical kinetics equations.
ВведениеДиффузия во многих системах является одним из фундаментальных процессов, определяющих поведение этих систем, а диффузионный подход позволяет изучать эти системы на уровне сплошной среды. Однако классическая диффузия, для которой поток пропорционален градиенту концентрации с некоторым постоянным коэффициентом, не всегда соответствует действительности. В таких случаях диффузионный подход нуждается в модификациях [4], или становится неприменимым.
Наиболее точным способом вычисления более сложных коэффициентов диффузии является использование кинетических уравнений (при условии достаточной точности коэффициентов в самих кинетических уравнениях). Примерами применения такой методики являются вывод коэффициентов диффузии в [2] и кинетически согласованные разностные схемы [4].
Одной из систем, в которых классический диффузионный подход неприменим, является неидеальный решеточный газ [5], [6], [7]. В этих работах, в частности, проводилось исследование зависимости коэффициентов диффузии в решеточном газе от концентраций веществ. Эти зависимости являются существенно непостоянными и нелинейными. В моделях решеточного газа при выводе коэффициентов диффузии обычно делается предположение о малости градиентов концентраций [6].
Однако градиенты концентраций не всегда можно считать малыми. В [8] автором выведены выражения для потока мигрирующих частиц и для коэффициентов диффузии без предположения о малости градиентов. За основу взяты уравнения химической кинетики [5], [6], [7]. В [8] учитывается также несовпадение направлений градиентов и потоков, т.е. полученные коэффициенты диффузии являются матричными и зависят от концентраций адсорбированных веществ и от их градиентов. В [9], [10], [11] проводилось исследование в приближении среднего поля и квазихимическом (см. [5], [6]). Исследуем полученные коэффициенты в этих приближениях более подробно.
Диффузия в решеточном газеНеидеальный решеточный газ представляет собой систему взаимодействующих частиц, которые могут находиться в узлах регулярной пространственной решетки. Решеточный газ может быть двумерным (например, слой адсорбата на поверхности монокристалла) или трехмерным (например, газ, абсорбированный твердым телом).
Состояние решеточного газа задается числами заполнения ni, где i - индекс узла решетки. Значение ni равно номеру химической компоненты, которой занят узел (0 - для свободного узла). Числа заполнения изменяются за счет происходящих по определенным статистическим законам прыжков частиц в соседние узлы, обменов с газовой фазой и реакций между частицами, находящимися в соседних узлах.
Описание решеточного газа как сплошной среды осуществляется с помощью уравнений реакции-диффузии [7]:
где N - число компонент, ![]() - плотность n-й компоненты, функция
- плотность n-й компоненты, функция ![]() описывает обмен с газовой фазой и химические реакции. Поток
описывает обмен с газовой фазой и химические реакции. Поток ![]() определяется в соответствии с законом Фика:
определяется в соответствии с законом Фика:
![]()
Вывод выражений для потока и коэффициентов диффузии
При описании состояния решеточного газа на уровне уравнений химической кинетики используются следующие переменные [5], [6], [12]: ![]() - вероятность заполнения i-го узла n-ой компонентой,
- вероятность заполнения i-го узла n-ой компонентой, ![]() - вероятность одновременного заполнения i-го узла n-ой компонентой, а j-го узла m-ой компонентой для всех пар соседних узлов. Могут рассматриваться и более чем парные вероятности, но в дальнейшем это не учитывается, так как не вносит качественных изменений в схему вывода коэффициентов диффузии. В общем виде уравнения химической кинетики для решеточного газа являются обыкновенными дифференциальными уравнениями и имеют вид [7]
- вероятность одновременного заполнения i-го узла n-ой компонентой, а j-го узла m-ой компонентой для всех пар соседних узлов. Могут рассматриваться и более чем парные вероятности, но в дальнейшем это не учитывается, так как не вносит качественных изменений в схему вывода коэффициентов диффузии. В общем виде уравнения химической кинетики для решеточного газа являются обыкновенными дифференциальными уравнениями и имеют вид [7]
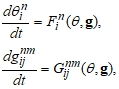 (3)
(3)
где индексы ![]() пробегают все значения, для которых введены соответствующие переменные. Хотя формально в правые части входят полные векторы
пробегают все значения, для которых введены соответствующие переменные. Хотя формально в правые части входят полные векторы ![]() , реально в число аргументов функций
, реально в число аргументов функций ![]() входят лишь переменные, относящиеся к узлам решетки, находящимся вблизи узлов
входят лишь переменные, относящиеся к узлам решетки, находящимся вблизи узлов ![]() .
.
Можно предположить, что локальные парные вероятности ![]() устанавливаются существенно быстрее, чем происходит процесс переноса массы по поверхности. Поэтому для вывода коэффициентов диффузии можно вместо соответствующего дифференциального уравнения рассматривать уравнение
устанавливаются существенно быстрее, чем происходит процесс переноса массы по поверхности. Поэтому для вывода коэффициентов диффузии можно вместо соответствующего дифференциального уравнения рассматривать уравнение
![]() (4)
(4)
Будем считать, что уравнение (4) однозначно разрешимо относительно переменных g. Для большинства приближений это так, либо переменные g явно выражаются через переменные ![]() . Поэтому определена функция
. Поэтому определена функция ![]() . Подстановка этой функции в первое уравнение системы (3) приводит к уравнению относительно плотностей заполнения:
. Подстановка этой функции в первое уравнение системы (3) приводит к уравнению относительно плотностей заполнения:
![]() (5)
(5)
где ![]() - множество ближайших соседей узла i,
- множество ближайших соседей узла i, ![]() - скорости миграции n-ой компоненты из узла i в узел j и из узла j в узел i, соответственно. Функция
- скорости миграции n-ой компоненты из узла i в узел j и из узла j в узел i, соответственно. Функция ![]() описывает обмен с газовой фазой и химические реакции; она также представляет собой сумму скоростей элементарных процессов.
описывает обмен с газовой фазой и химические реакции; она также представляет собой сумму скоростей элементарных процессов.
Пусть в узле i заданы концентрации ![]() и их градиенты
и их градиенты ![]() . Тогда с помощью линейной экстраполяции могут быть найдены концентрации в любом узле j из окрестности этого узла:
. Тогда с помощью линейной экстраполяции могут быть найдены концентрации в любом узле j из окрестности этого узла:
![]() (7)
(7)
где ![]() - вектор из узла i в узел j; (,) – скалярное произведение. Подстановка (7) в (6) позволяет выразить
- вектор из узла i в узел j; (,) – скалярное произведение. Подстановка (7) в (6) позволяет выразить![]() через
через ![]() . Выражение для потока может быть получено суммированием всех потоков в узле i:
. Выражение для потока может быть получено суммированием всех потоков в узле i:
![]() (8)
(8)
Отсюда коэффициенты диффузии могут быть вычислены как производные от потока по градиенту, взятые с обратным знаком:
Выражения (8) и (9) имеют отличия от классического случая (1), (2). Поток (8), в отличие от (2), зависит от градиента нелинейно и, вообще говоря, должен быть непосредственно подставлен в выражение (1). Для того чтобы выяснить качественные отличия между полученным выражением для потока (8) и выражением (2), удобнее рассматривать коэффициенты диффузии (9). В силу (8), выражения (9) зависят не только от концентраций, но и от их градиентов. Более того, коэффициенты диффузии являются линейными операторами, т.е. направление потока может отличаться от направления градиента концентрации даже в случае однокомпонентного газа.
Зависимость коэффициентов диффузии от величины градиента позволяет сделать вывод о том, существенна ли подстановка в уравнение (1) выражения (8), а не произведения коэффициентов диффузии (9) на градиенты концентраций. Существенных отличий от вариантов диффузии, рассмотренных в [6], [7], естественно ожидать при больших градиентах и сильных латеральных взаимодействиях.
Будем считать, что ось абсцисс параллельна линиям решетки. Направление потока, противоположное градиенту, назовем нормальным. Угол между направлением потока и положительным направлением оси абсцисс обозначим β, а угол между нормальным направлением и положительным направлением оси абсцисс - ![]() . Угол между положительным направлением оси абсцисс и направлением градиента, соответственно, равен
. Угол между положительным направлением оси абсцисс и направлением градиента, соответственно, равен ![]() . Угол между направлением градиента и направлением потока
. Угол между направлением градиента и направлением потока ![]() .
.
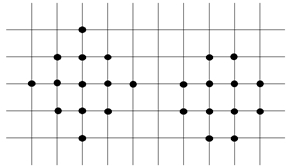
Будем рассматривать поток не в узле кристаллической решетки, а в центре ячейки. При этом шаблон, который необходимо учитывать, состоит не из тринадцати точек, а из двенадцати, и он более компактный, что существенно при изучении больших градиентов концентраций (рис. 1). Концентрацию в центре шаблона обозначим A0. Четыре узла решетки, находящиеся в углах центральной ячейки этого шаблона, будем называть внутренними. Остальные восемь узлов – внешними. Будем считать, что в центре шаблона находится начало координат.
а) б)
Рис. 1 – а) Шаблон для потока в узле кристаллической решетки; б) Шаблон для потока в центре ячейки кристаллической решетки
Будем считать, что ![]() , а величина градиента находится в пределах
, а величина градиента находится в пределах ![]() . В этом случае концентрации во внутренних узлах шаблона изменяются в интервале (0;1). В случае большого градиента формула (7) может выдавать выходящие за пределы физически допустимых значения концентраций во внешних узлах (рис. 2). Вероятности, выходящие за пределы интервала (0;1), можно, например, заменять на или , но такое приближение не очень точное и не везде дифференцируемое. Другой вариант – заменять значения на максимальные и минимальные концентрации во внутренних точках шаблона. Реальные значения концентраций обычно находятся между этими двумя приближениями. Можно также построить гладкую функцию со значениями, заключенными в этом промежутке. В данной работе используется следующая функция:
. В этом случае концентрации во внутренних узлах шаблона изменяются в интервале (0;1). В случае большого градиента формула (7) может выдавать выходящие за пределы физически допустимых значения концентраций во внешних узлах (рис. 2). Вероятности, выходящие за пределы интервала (0;1), можно, например, заменять на или , но такое приближение не очень точное и не везде дифференцируемое. Другой вариант – заменять значения на максимальные и минимальные концентрации во внутренних точках шаблона. Реальные значения концентраций обычно находятся между этими двумя приближениями. Можно также построить гладкую функцию со значениями, заключенными в этом промежутке. В данной работе используется следующая функция:
![]() (10)
(10)
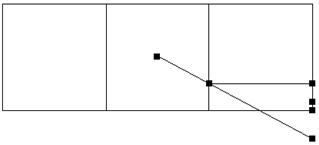
Рис. 2 – Варианты вычисления концентрации во внешних узлах
Совпадение направления градиента и линий решетки
Будем рассматривать квадратную решетку, узлы которой некоторым образом пронумерованы. Пусть слой является однокомпонентным (компонента A), и направление градиента концентрации совпадает с направлением линий решетки. В этом случае поток в однокомпонентном слое из узла i в узел j в приближении среднего поля может быть записан следующим образом:
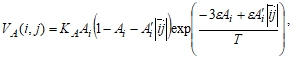 (11)
(11)
где ![]() - вероятность заполнения узла i;
- вероятность заполнения узла i; ![]() - вектор, соединяющий узел i с узлом j;
- вектор, соединяющий узел i с узлом j; ![]() - множитель, учитывающий предэкспоненту и энергию активации; ε - параметр латерального взаимодействия; T - температура. Встречный поток из узла j в узел i равен
- множитель, учитывающий предэкспоненту и энергию активации; ε - параметр латерального взаимодействия; T - температура. Встречный поток из узла j в узел i равен
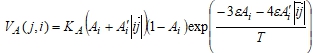 (12)
(12)
![]() (14)
(14)
Множитель ![]() , которым мы пренебрегли, пропорционален разности концентраций
, которым мы пренебрегли, пропорционален разности концентраций ![]() . Таким образом, пренебрегать этим множителем можно только в том случае, если
. Таким образом, пренебрегать этим множителем можно только в том случае, если
Условие (15) может также не выполняться, если ![]() достаточно мало, но испытывает достаточно большие относительные изменения от узла к узлу. В этом случае, если считать
достаточно мало, но испытывает достаточно большие относительные изменения от узла к узлу. В этом случае, если считать ![]() , то значения экспонент в выражениях (11) и (12) можно считать приблизительно равными единице, а коэффициенты диффузии - равными
, то значения экспонент в выражениях (11) и (12) можно считать приблизительно равными единице, а коэффициенты диффузии - равными ![]() . Поэтому условие применимости выражения (14) принимает вид:
. Поэтому условие применимости выражения (14) принимает вид:
На рис. 3 приведена зависимость коэффициента диффузии от величины градиента для различных значений параметров. Излом в точке ![]() соответствует достижению в крайних точках шаблона значений концентрации 0 и 1. Этот излом особенно заметен при положительном параметре латерального взаимодействия.
соответствует достижению в крайних точках шаблона значений концентрации 0 и 1. Этот излом особенно заметен при положительном параметре латерального взаимодействия.
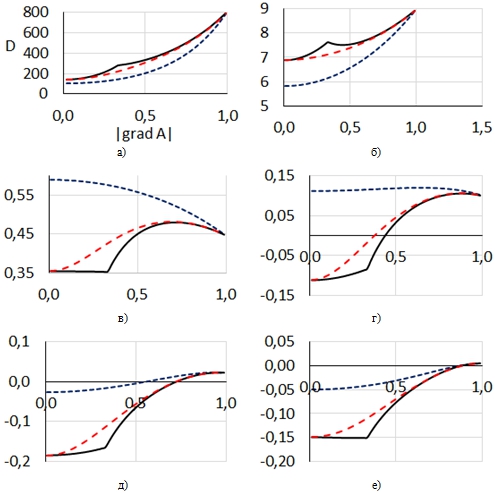
Рис. 3 – Зависимость коэффициента диффузии от величины градиента при совпадении направления градиента и направления линий решетки. ![]()
Сплошная линия – 1-й способ вычисления концентраций во внешних узлах, пунктир – второй способ, длинный пунктир – третий способ
Излом в точке ![]() происходит в сторону графика, построенного по второму способу вычисления концентраций во внешних узлах шаблона. При
происходит в сторону графика, построенного по второму способу вычисления концентраций во внешних узлах шаблона. При ![]() этот способ дает меньшее значение коэффициента диффузии (а,б), а при
этот способ дает меньшее значение коэффициента диффузии (а,б), а при ![]() – большее (в-е). Отметим также, что при стремлении градиента к нулю значения коэффициента диффузии для рассматриваемых способов вычисления концентраций во внешних узлах шаблона могут значительно различаться.
– большее (в-е). Отметим также, что при стремлении градиента к нулю значения коэффициента диффузии для рассматриваемых способов вычисления концентраций во внешних узлах шаблона могут значительно различаться.
Коэффициент диффузии может считаться приблизительно постоянным лишь при значениях градиента <0.1. При значениях >0.1, а особенно при значениях ~1, зависимость коэффициента диффузии от величины градиента очень существенна. Коэффициент диффузии может, как возрастать, так и убывать с ростом величины градиента, однако характерно наличие участка заметного роста коэффициента, означающего что при очень большом градиенте система стремится градиент уменьшить. Это можно видеть из рисунков (г-е), где коэффициент переходит из отрицательной области в положительную. Отрицательное значение коэффициента соответствует тому, что решеточный газ будет собираться в капли. Но если граница капель станет слишком узкой, то она будет “размазываться” диффузией.
Отклонение направления градиента от линий решетки
Пусть направление градиента концентрации не совпадает с направлением линий кристаллической решетки, тогда поток определяется выражением:
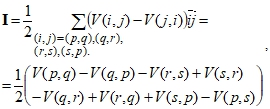 (17)
(17)
где ![]() - номера узлов кристаллической решетки, находящихся в углах рассматриваемой ячейки. Выражения
- номера узлов кристаллической решетки, находящихся в углах рассматриваемой ячейки. Выражения ![]() принимают вид:
принимают вид:
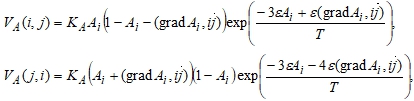 (18)
(18)
где ![]() - градиент концентрации в узле i. Коэффициент диффузии в этом случае является матричным:
- градиент концентрации в узле i. Коэффициент диффузии в этом случае является матричным:
![]() (19)
(19)
На рис. 4 приведены графики зависимости величины γ от угла α для различных значений параметров. Они являются нелинейными и немонотонными. Присутствуют зависимости двух типов. На рис. 3 (а-в) направление потока при ![]() совпадает с направлением градиента (коэффициент диффузии, соответственно, отрицателен). В промежутке между этими значениями α наблюдается отличие угла β от угла
совпадает с направлением градиента (коэффициент диффузии, соответственно, отрицателен). В промежутке между этими значениями α наблюдается отличие угла β от угла ![]() . Можно видеть, также, что результаты, получаемые третьим способом вычисления концентраций во внешних узлах могут выходить за пределы, задаваемые первыми двумя способами.
. Можно видеть, также, что результаты, получаемые третьим способом вычисления концентраций во внешних узлах могут выходить за пределы, задаваемые первыми двумя способами.
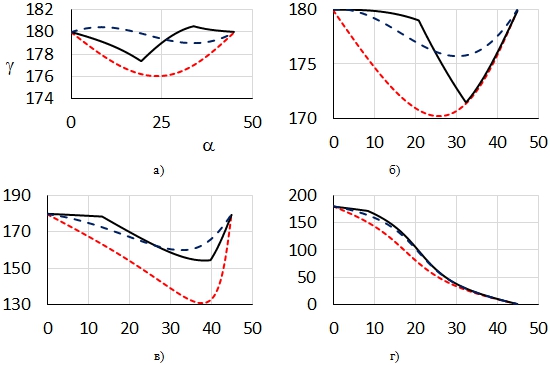
Рис. 4 – Угол между направлением потока и нормальным направлением в зависимости от угла между нормальным направлением и направлением линий решетки. ![]()
На рис. 4 (г) направление потока изменяется от совпадающего с направлением градиента при ![]() до нормального при
до нормального при ![]() . Из этого, в частности, следует возможность ортогонального направления потока по отношению к направлению градиента.
. Из этого, в частности, следует возможность ортогонального направления потока по отношению к направлению градиента.
Обсудим это явление более подробно. Заметим, что фактически поток (17) является суммой двух ортогональных потоков. Далее, из формулы (18) следует, что на величину потока в данном направлении влияет лишь проекция градиента на это направление. Таким образом, поток расщепляется на два одномерных потока, каждый из которых подчиняется закону (11)-(13), где производную ![]() надо брать в направлении соответствующей оси координат.
надо брать в направлении соответствующей оси координат.
Это позволяет объяснить возможность ортогонального направления потока по отношению к градиенту. Действительно, как следует из рис. 3, знак коэффициента диффузии может изменяться в зависимости от градиента. При вращении постоянного по величине вектора градиента от ![]() до
до ![]() величина проекции градиента на ось ординат изменяется от
величина проекции градиента на ось ординат изменяется от ![]() , а величина проекции градиента на ось абсцисс изменяется от
, а величина проекции градиента на ось абсцисс изменяется от ![]() . Если на этих интервалах коэффициент диффузии соответствующим образом меняет знак, то становятся возможными любые углы между направлениями потока и градиента.
. Если на этих интервалах коэффициент диффузии соответствующим образом меняет знак, то становятся возможными любые углы между направлениями потока и градиента.
В более точных приближениях такое расщепление, по-видимому, невозможно из-за наличия нелинейных связей между корреляционными функциями. Однако это не исключает возможности любых углов между направлениями потока и градиента. Действительно, если, например, при малых значениях градиента коэффициент диффузии отрицателен, то при больших значениях градиента он может стать положительным, так как система будет стремиться уменьшить слишком большой градиент. Таким образом, при некотором значении градиента коэффициент диффузии будет равен нулю. Причем эти значения могут различаться для ![]() и
и ![]() . Выбрав значение градиента так, чтобы коэффициент обращался в нуль в интервале
. Выбрав значение градиента так, чтобы коэффициент обращался в нуль в интервале ![]() , можно также получить любые углы между направлениями потока и градиента. На рис. 5 показан пример такой ситуации для одного из вариантов учета парных вероятностей (квазихимические вероятности [6]). В приведенном примере изменение угла
, можно также получить любые углы между направлениями потока и градиента. На рис. 5 показан пример такой ситуации для одного из вариантов учета парных вероятностей (квазихимические вероятности [6]). В приведенном примере изменение угла ![]() произошло при значении градиента 0.325. И обусловлено это явление зависимостью коэффициента диффузии от величины и направления градиента.
произошло при значении градиента 0.325. И обусловлено это явление зависимостью коэффициента диффузии от величины и направления градиента.
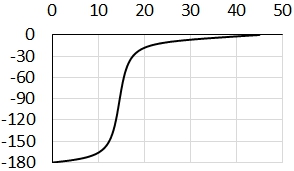
Рис. 5 – Угол между направлением потока и нормальным направлением в зависимости от угла между нормальным направлением и линиями решетки. ![]() третий способ вычисления концентраций
третий способ вычисления концентраций
Ортогональность потока и градиента может, например, приводить к образованию капель поверхностной жидкости различной формы. Если при угле ![]() поток и градиент ортогональны, то они ортогональны также при
поток и градиент ортогональны, то они ортогональны также при ![]() . Таким образом, если на поверхности имеется круглая капля, то на ее границе есть восемь точек, в которых вещество диффундирует вдоль границы. И, следовательно, капля будет деформироваться.
. Таким образом, если на поверхности имеется круглая капля, то на ее границе есть восемь точек, в которых вещество диффундирует вдоль границы. И, следовательно, капля будет деформироваться.
Заключение
Полученные результаты свидетельствуют о существенном отличий коэффициентов диффузии при больших градиентах концентрации. При больших градиентах зависимость потока от градиента нелинейна, и лучше пользоваться более точным выражением (8) или коэффициентами (9), а не (2).
Качественные свойства диффузии в решеточном газе при больших градиентах концентраций существенно отличаются от свойств диффузии с постоянным коэффициентом и коэффициентом, зависящим только от концентраций. Представляет интерес и то, как эти свойства отражаются на протекании поверхностных явлений. Прежде всего, это относится к процессам, в которых есть узкая граница между концентрациями веществ.
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы / References
- Ландау Л.Д. Статистическая физика / Ландау Л.Д., Лифшиц Е.М. – М: Наука. – 1964. – 567 c.
- Левич В.Г. Курс теоретической физики. т. 1 / Левич В.Г. – М: Физматгиз. – 1962. – 695 c.
- Хилл Т. Статистическая механика / Хилл Т. – М: ИЛ. – 1960. – 486 c.
- Елизарова Т.Г. Кинетические алгоритмы для расчета гидродинамических течений / Елизарова Т.Г., Четверушкин Б.Н. // ЖВМ и МФ. – 1985. – Т. 25. – N – С. 1526.
- Товбин Ю.К. Теория физико-химических процессов на границе газ-твердое тело / Товбин Ю.К. – М.: Наука. – 1988. – 285 c.
- Жданов В.П. Элементарные физико-химические процессы на поверхности / Жданов В.П.– Новосибирск: “Наука” Сиб. отд. – 1988. – 319 c.
- Еленин Г.Г. Математическое моделирование гетерогенных каталитических реакций на гранях монокристаллов благородных металлов. Част I. Сверхструктуры и фазовые переходы / Еленин Г.Г. // Российский химический журнал. – 1996. – N – С. 19-50.
- Трощиев Ю.В. О коэффициентах диффузии в неидеальном решеточном газе при больших градиентах концентраций / Трощиев Ю.В. – Труды факультета ВМК, Прикладная математика и информатика. – М: Диалог-МГУ. – 1999. – N – С. 51-57.
- ТрощиевЮ.В. Исследование матричных коэффициентов диффузии в решеточном газе при больших градиентах концентрации в приближении среднего поля / ТрощиевЮ.В.// Препринт. – М: МАКС Пресс. – 2003. – 10 c.
- ТрощиевЮ.В. Матричные коэффициенты диффузии на квадратной решетке / ТрощиевЮ.В. // Ломоносовские чтения. – Москва, МГУ, ф-т ВМК. – Апрель 2006.
- Трощиев Ю.В. Матричные коэффициенты диффузии в решеточном газе при больших градиентах концентраций (квазихимическое приближение) / Трощиев Ю.В.// Тихоновские чтения, Секция Математическое моделирование и вычислительные методы. – Москва, МГУ, ф-т ВМК. – 29 октября – 2 ноября 2007.
- Еленин Г.Г. Математическое моделирование процесса образования островковых структур на поверхности монокристалла / Еленин Г.Г., Макеев А.Г. // Математическое моделирование. –1991. – N – С. 29.
Список литературы на английском языке / References in English
- Landau L.D. Statisticheskaya fizika [Statistical Physics] / L.D. Landau, E.M. Lifshitz. // Butterworth-Heinemann. – 1980. – V. 5. ISBN 978-0-7506-3372-7.
- Levich B.G. Kurs teoreticheskoj fiziki [Theoretical Physics]. V. 1 / B.G. Levich.– Мoscow: PhysMathGIz. – 1962. – 695 p. [in Russian]
- Hill T.L. Statisticheskaya mekhanika [Statistical mechanics]. / T.L. Hill. – New York a. o., McHaw-Hill. – 1956.
- Elizarova T.G. Kineticheskie algoritmy dlya rascheta gidrodinamicheskih techenij [Kinetic algorithms for calculating gas dynamic flows]. / T.G. Elizarova, B.N. Chetverushkin. // USSR Computational Mathematics and Mathematical Physics. – V. 25. – Issue 5. – 1985. – P. 164–169. [in Russian]
- Tovbin Yu K. Teoriya fiziko-himicheskih processov na granice gaz-tverdoe telo [Theory of Physical Chemistry Processes at a Gas-Solid Interface] (Advances in Science and Technology in the USSR) / Yu K. Tovbin – Crc Pr I Llc. – 1991. – 349 p. [in Russian]
- Zhdanov V.P. Elementarnye fiziko-himicheskie processy na poverhnosti [Elementary Physicochemical Processes on Solid Surfaces] / V.P. Zhdanov. – Springer US. – 1991. DOI: 10.1007/978-1-4899-2373-8. [in Russian]
- Elenin G.G. Matematicheskoe modelirovanie geterogennyh kataliticheskih reakcij na granyah monokristallov blagorodnyh metallov. CHast I. Sverhstruktury i fazovye perekhody [Mathematical modeling of heterogeneous catalytic reactions on the faces of crystals of precious metals. Part I. Superstructures and phase transitions] / G.G. Elenin. // Russian Chemical Journal. – 1996. – N 2. – P. 19-50. [in Russian]
- Troshchiev Yu.V. O koefficientah diffuzii v neideal'nom reshetochnom gaze pri bol'shih gradientah koncentracij [Diffusion coefficients in a nonideal lattice gas with high concentration gradients]. – Computational Mathematics and Modelling / Yu.V. Troshchiev. – 2000. – V. 11. – N 1. – P. 40-45. DOI: 10.1007/BF02359062 [in Russian]
- Troshchiev Yu.V. Issledovanie matrichnyh koefficientov diffuzii v reshetochnom gaze pri bol'shih gradientah koncentracii v priblizhenii srednego polya [Investigation of Matrix Diffusion Coefficients in Lattice Gas under the Large Concentration Gradients in Mean Field Approximation]. – Preprint / Yu.V. Troshchiev. – Moscow: MAKS Press. – 2003. – 10 p. [in Russian]
- Troshchiev Yu.V. Matrichnye koefficienty diffuzii na kvadratnoj reshetke [The Matrix Diffusion Coefficients at Square Lattice] / Yu.V. Troshchiev. // Sci. Conf. Lomonosov Readings. – Moscow, MSU, Dept. CMC. – April 2006. [in Russian]
- Troshchiev Yu.V. Matrichnye koefficienty diffuzii v reshetochnom gaze pri bol'shih gradientah koncentracij (kvazihimicheskoe priblizhenie) [Matrix Diffusion Coefficients in Lattice Gas under Large Concentration Gradients (Quasi-chemical Approximation)] / Yu.V. Troshchiev // Tihonovskie chteniya, Sekciya Matematicheskoe modelirovanie i vychislitel'nye metody [Sci. Conf. Tikhonov Readings, Section Mathematical Modeling and Numerical Methods] – Moscow, MSU, Dept. CMC. – October 29– November 2 2007. [in Russian]
- Elenin G.G. Matematicheskoe modelirovanie processa obrazovaniya ostrovkovyh struktur na poverhnosti monokristalla [Mathematical Modeling of the Process of Island Structure Formation on the Single Cristal Surface] / G.G. Elenin, A.G. Makeev. – Matematicheskoe modelirovanie [Mathematical Modeling]. – 1991. – N 7. – p. 29. [in Russian]
