LINGUISTIC ANALYSIS OF STRUCTURAL AND CONCEPTUAL COHERENCE OF TEXT IMPLICATES IN THE CONTEXT OF THE SEARCH FOR CONTRADICTIONS IN FUZZY RULE BASE
Поспелова Л.Я.
ORCID: 0000-0002-5037-4161, Кандидат технических наук, доцент, Вычислительный центр им. А.А. Дородницына Федерального исследовательского центра «Информатика и управление» Российской академии наук
ЛИНГВИСТИЧЕСКИЙ АНАЛИЗ СТРУКТУРНОЙ И СОДЕРЖАТЕЛЬНОЙ СВЯЗНОСТИ ТЕКСТОВЫХ ИМПЛИКАТОВ В КОНТЕКСТЕ ПОИСКА ПРОТИВОРЕЧИЙ В НЕЧЕТКОЙ БАЗЕ ПРАВИЛ
Аннотация
Описана предлагаемая методика выявления и оценки разного рода противоречий в нечеткой многоуровневой системе продукций. Показана продуктивность применения методики для проведения семантического анализа структурной и содержательной связности особого рода текстов, представленных в виде наборов текстовых импликатов. Поскольку в процессе ревизии прикладных баз знаний множество эксплицитных и имплицитных убеждений абстрактного рационального субъекта в идеале должно поддерживать разумную меру логической непротиворечивости и замкнутости относительно операций логического вывода, нечеткая логико-лингвистическая система может служить полигоном для экспериментов по выявлению логических и концептуальных противоречий.
Ключевые слова: нечеткая база правил, логическое противоречие, концептуальное противоречие, имплицитное утверждение, логическая инференция.Pospelova L.Ya.
ORCID: 0000-0002-5037-4161, PhD in Engineering, Associate professor, Senior Researcher, Dorodnicyn Computing Centre, Federal Research Center “Computer Science and Control” of Russian Academy of Sciences
LINGUISTIC ANALYSIS OF STRUCTURAL AND CONCEPTUAL COHERENCE OF TEXT IMPLICATES IN THE CONTEXT OF THE SEARCH FOR CONTRADICTIONS IN FUZZY RULE BASE
Abstract
Described the proposed methodology for the identification and evaluation of various kinds of contradictions in the fuzzy multi-level production system. Shown the efficiency of application of the method to conduct a semantic analysis of structural and conceptual coherence of specific kinds of texts presented in the form of sets of text implicates. As a result of the revision of the applied knowledge bases, the set of explicit and implicit beliefs of an abstract rational subject must maintain a reasonable measure of logical consistency and closure concerning the operations of logical inference, therefor a fuzzy logic-linguistic system may serve as a testing ground for experiments on the identification of logical and conceptual contradictions.
Keywords: fuzzy rule base, logical contradiction, conceptual contradiction, implicit statement, logical inference.Задача интеллектуализации сетевого пространства [1, с. 1297; 4, с. 138] вернула усилия математиков, лингвистов, философов на этап изучения и моделирования механизмов человеческого мышления, этап поиска способов компьютерного представления знаний и убеждений. Наблюдаемая в настоящее время неудовлетворительная степень релевантности запросов обусловлена трудностями формального описания концептов и концептуальных отношений проблемных областей: прикладные онтологии, учитывающие специфику принятия решений компьютером, имеют дело с реальностью сконструированной, а программы систем, основанных на знаниях, строятся на базе той или иной разновидности неклассической логики. В философских трудах разрабатываются эпистемологические концепции изменения систем знаний [4, с. 136], математики исследуют логику убеждений и эпистемологическую логику знаний, паранепротиворечивые логики, дескриптивные логики как основы языков прикладных онтологий [1, с. 1297].
Возросшие требования государственных и общественных структур к качеству комплексной филологической экспертизы текстов активизировали исследования в области семантического и концептуального анализа. Особое внимание уделяется импликативным причинно-следственным отношениям между концептами-понятиями [5, с. 4] и их роли в ходе операций семантического вывода с целью извлечения глубинной (имплицитной) информации [2, с. 1; 4, с. 138]. В указанных работах можно проследить прямую аналогию между текстовыми импликатами и аксиомами логического следования в системах продукций, между процессом извлечения имплицитной информации из набора импликативных суждений (процессом формально-логической инференции) и экспертным логическим выводом. Например, следствия, рассматриваемые лингвистами как имплицитные части высказываний, могут выводиться из семантики на одном, двух или многих шагах рассуждений. Чем короче цепочка вывода, тем ближе следствия находятся к поверхностной, эксплицитной части семантики. На длинных цепочках вывода следствия опустятся на глубинные слои плана содержания и будут рассматриваться не как обязательные пропозиции, но как некие факультативные предположения [2, с. 4] – этот вывод вызывает вполне объяснимый интерес разработчиков баз нечетких правил, заинтересованных в уменьшении меры внутренней неопределенности объекта управления по отношению к выводимому свойству этого объекта..
Обобщенный теоретический подход активно изучает противоречия в онтологиях, выявляет причины возникновения противоречивости при ревизии рациональным субъектом собственных понятий и убеждений [1, с. 1298, 6, с. 138]. Практической стороной занимается прикладная когнитология.
В инженерии знаний концептуализации редко поднимаются до описания абстрактных знаний (философских онтологий верхнего уровня), поскольку суть современного онтологического поворота (смещение интереса от эпистемологии к онтологии) [8, с. 2] в том, что для отображения знаний в эксплицитно-имплицитных формах исследователи прибегают к огрубленным и идеализированным конструкциям, их интересует не интерпретация, не суть вещей, а то, как они профессионально используются на практике.
Наиболее остро стоит проблема повторного использование онтологий в Semantic Web-приложениях [1], когда в результате добавления новых аксиом, ревизии или удаления существующих аксиом пользователи могут обнаружить, что новые онтологии стали противоречивыми. Необходимость выработки единой фундаментальной основы, поддерживающей формальное определение противоречия и отрицания и позволяющей усилить языки онтологий в части представления аксиомы отрицания является одной из первоочередных задач математиков и лингвистов. Для онтологий, основанных на дескриптивных логиках и постулатах рациональности [4, с. 139], авторы [1, с. 1297] предлагают различать два вида противоречий: несогласованность и классическую противоречивость, естественным образом появляющихся в динамических базах знаний. Если классическая (логическая) противоречивость может быть выявлена при тестировании системы на замкнутость относительно логического следования [4, с. 137; 6, с. 186; 7, с. 136], то концептуальное противоречие не поддается формализации в рамках классической логики. Поскольку в реальных приложениях всякая онтология подразумевается нечеткой, развитие конструктивных методов выявления разного рода противоречий является актуальной прикладной задачей.
В настоящей работе объект исследования сужен до статических нечетких многоуровневых систем продукций, для которых метод и алгоритм автоматического выявления логических противоречий на прагматическом функциональном уровне логического вывода описан в [7, с. 136]. Еще одно сужение связано с применением законов «материальной импликации» (ex falso quodlibet - «из ложного - что угодно») в рамках паранепротиворечивой логики.
Описанный в [7, с. 136] алгоритм выявления логических противоречий в нечетких системах правил использует преимущества динамического подхода [6, с. 185]. Отмечено, что для нечетких баз правил нельзя требовать замкнутости множества правил-аксиом относительно логического следования. Например, метод доказательства теорем («reduction ad absurdum») в формализмах классических логик, проверяющий на каждом шаге, не свелось ли результирующее высказывание к пустому множеству [6, с. 187], в нечетком выводе удовлетворительно работать уже не будет. На неуниверсальность закона непротиворечия указывалось еще в работах русского логика Васильева Н.А.: содержательный анализ природы отрицания показал, что единственным источником отрицания является эмпирическая несовместимость признаков. Степень принадлежности объекта управления сразу нескольким несовместимым классам (например, «Значительное падение» и «Значительный рост») по отношению к нечеткой выходной переменной (например, «Прогноз курса национальной валюты») есть степень нечеткости суждения «Пересечение всех результатов нечеткого вывода множества применимых при некотором входе правил есть пустое множество» (носитель результата-выхода – непересекающиеся интервалы).
Исследуемая система правил является системой утверждений логического следования. Нечеткие правила (импликативные отношения между суждениями) могут быть эксплицитными, (явными, выражающими поверхностное содержание) или имплицитными (выражающими скрытый, глубинный слой содержания, его подтекст) [2, с. 1; 5, с. 4]. В процессе логического вывода экономный (имплицитный) способ отображения содержания эксплицируется в развернутое, явно выраженное высказывание-импликацию. Значения входные переменных являются самыми эксплицитными (соответствующими действительности) частями семантики высказывания в конкретном сеансе экспертного вывода. Компиляция многоуровневых иерархических баз правил может рассматриваться как выведение всех правил-импликаций на эксплицитный уровень. При поиске противоречий в иерархических нечетких системах продукций выход в виде нечетких переменных одного уровня напрямую передается на входы правил следующего уровня иерархии без дефаззификации и фаззификации. Поэтому при описании промежуточных (имплицитных) переменных достаточно обозначить только терм-множества.
Итак, пусть скомпилированная база правил содержит нечетких импликаций для эксплицитных входов и одного выхода:
где: ![]() – множество входных переменных, заданных на своих универсальных множествах
– множество входных переменных, заданных на своих универсальных множествах ![]() ; нечеткие термы
; нечеткие термы ![]() – элементы терм-множеств:
– элементы терм-множеств: ![]() ; принадлежность терма
; принадлежность терма ![]() соответствующему универсальному множеству
соответствующему универсальному множеству ![]() задается функцией принадлежности
задается функцией принадлежности ![]() ;
; ![]() – выходная переменная, заданная на универсе
– выходная переменная, заданная на универсе ![]() , её нечеткие термы
, её нечеткие термы ![]() имеют функции принадлежности
имеют функции принадлежности ![]() .
.
Принятые форматные ограничения (1) не помешают нашим рассуждениям о противоречивости даже иерархических НБЗ. Переход к скомпилированным продукциям, у которых будут отсутствовать имплицитные лингвистические переменные, произойдет без потери экспертной информации и без ущерба для рассмотрения идеи метода.
Логические противоречия выявляются при оценке степени замкнутости системы правил относительно логического следования. В абдукции истинность с заключения правила Rt переносится на посылки:
![]()
Оправдательный механизм абдукции используется при последовательном тестировании каждой импликации. Эксплицитным входом служит «зашумленный» сигнал, который описывается нечеткими множествами, совпадающими с условиями проверяемого правила, например, правила R1:
![]() (2)
(2)
Для входа (2) для каждого из правил нечеткой базы знаний ![]() вычисляется нечеткая t- импликация Мамдани. В результате получим новую нечеткую переменную либо со «срезанной», либо с исходной функцией принадлежности терм-множеству выхода-заключения правила. Rt:
вычисляется нечеткая t- импликация Мамдани. В результате получим новую нечеткую переменную либо со «срезанной», либо с исходной функцией принадлежности терм-множеству выхода-заключения правила. Rt:
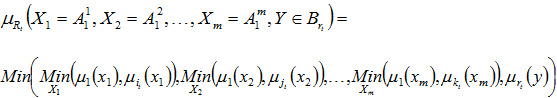
Мера применимости проверяемого правила R1 всегда будет максимальной при заданном «зашумленном» входе (2) с максимальным значением меры выполненности посылки данного правила. Функция принадлежности результата ![]() будет совпадать с
будет совпадать с ![]() , т.е. не будет «срезанной». Правило неприменимо, когда мера выполненности посылки равна нулю.
, т.е. не будет «срезанной». Правило неприменимо, когда мера выполненности посылки равна нулю.
Высокая мера возможности получения противоречивых, двусмысленных результатов нечеткого вывода будет зафиксирована, если для данного входа (2) нечеткой системы (1) найдется такое применимое правило R0, что результат исчисления нечеткой импликации ![]() для него будет в значительной мере принадлежать терму выхода
для него будет в значительной мере принадлежать терму выхода ![]() , который несовместим с термом-заключением
, который несовместим с термом-заключением ![]() тестируемого правила R1:
тестируемого правила R1:
![]()
Здесь ![]() – носитель нечеткого множества
– носитель нечеткого множества ![]() . На следующем шаге анализируются все носители нечетких множеств – результатов
. На следующем шаге анализируются все носители нечетких множеств – результатов ![]() . Противоречие в нечеткой базе правил будет иметь максимальную степень, если найдутся такие подмножества значений входных переменных, для которых будут участвовать в композиции (в нечетком агрегировании) только правила с несовместимыми заключениями (в рассмотренном примере это правила R1 и R0).
. Противоречие в нечеткой базе правил будет иметь максимальную степень, если найдутся такие подмножества значений входных переменных, для которых будут участвовать в композиции (в нечетком агрегировании) только правила с несовместимыми заключениями (в рассмотренном примере это правила R1 и R0).
Агрегированный нечеткий выход для заданного входа (2) исчисляется взятием максимального значения по всем результатам нечеткого вывода множества применимых правил ![]() . Функция принадлежности объединения этих нечетких подмножеств имеет вид:
. Функция принадлежности объединения этих нечетких подмножеств имеет вид:
![]() (3)
(3)
Эта функция определена на ![]() . Ее причудливый вид уже длительное время вызывает беспокойство у прикладников. Предложены десятки методов дефаззификации нечеткого множества
. Ее причудливый вид уже длительное время вызывает беспокойство у прикладников. Предложены десятки методов дефаззификации нечеткого множества ![]() . Но если функция (3) не унимодальна, локальные максимумы сравнимы по величине с глобальным и соответствуют противоречащим друг другу термам, а носитель вторичного нечеткого множества состоит из непересекающихся интервалов, то применение любого из известных методов даст результат дефаззификации, который вызовет оторопь: его трудно считать приемлемым значением выходной переменной.
. Но если функция (3) не унимодальна, локальные максимумы сравнимы по величине с глобальным и соответствуют противоречащим друг другу термам, а носитель вторичного нечеткого множества состоит из непересекающихся интервалов, то применение любого из известных методов даст результат дефаззификации, который вызовет оторопь: его трудно считать приемлемым значением выходной переменной.
На рис. 1 показан пример трансформации поверхности отклика в ответ на введение логического противоречия. На рис. 1.а представлена непротиворечивая и согласованная база правил. Рис. 1.б – поверхность отклика логически противоречивой базы правил (после дефаззификации центроидным методом). Рис. 1.в иллюстрирует поверхность отклика той же самой логически противоречивой базы правил, но после дефаззификации, учитывающей, что носитель вторичного нечеткого множества представлен непересекающимися интервалами. В логически противоречивой нечеткой базе правил поверхность отклика (б) имеет седловидную область неустойчивых решений. Надо иметь в виду, что поверхность отклика строится огрубленно, по результатам дефаззификации, когда вторичное нечеткое множество тем или иным методом отображается в число (точку поверхности). Если же обратиться ко всей нечеткой области отклика, то она предстанет в гипербрусе облаком с пустотами (в). Проекции пустот на оси дадут «опасные» интервалы значений некоторых входов.
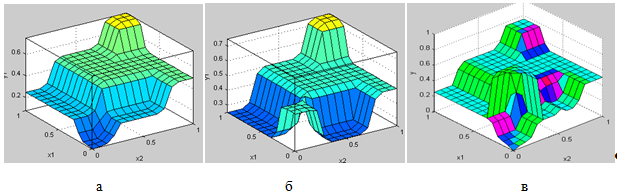
Рис. 1 – Поверхности отклика: а – непротиворечивая база правил; б – логически противоречивая, в – что и база правил (b), но после дефаззификации с учетом «пустот»
Рисунок 2 иллюстрирует поверхность отклика для системы правил, содержащей концептуальное противоречие. Например, правила:
Ri: IF(x1 is Low) AND (x2 is Low) THEN (y is Low)
Rk: IF(x1 is High) AND (x2 is High) THEN (y is Low)
формально не противоречат друг другу, но противоречия проявляются при конкретной интерпретации понятий. Когда на вход поступают переменные, принадлежащие с высокой степенью возможности термам «High», поверхность отклика предлагает неприемлемые (с содержательной точки зрения) значения выходной переменной. Область поверхности отклика для значений входных переменных, частично принадлежащих термам «High», демонстрирует заметную неустойчивость (см. рис. 2).
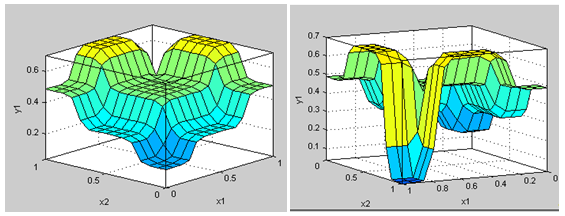
Рис. 2 - Поверхность отклика содержит концептуальное противоречие
Итак, предлагаемый метод фиксирует логическое или концептуальное противоречие, если в результате нечеткого вывода новое состояние системы станет недопустимым [6] для некоторой интерпретации (4):
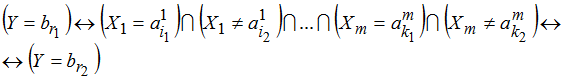 (4)
(4)
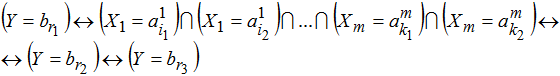 (5)
(5)
Если интерпретировать функцию принадлежности нечеткого результата как распределение возможностей (и как плотность меры неопределенности), то нечеткие cтепени допустимости противоречия, степени согласованности и достоверности результатов в (4) и (5) можно качественно и количественно оценивать путем анализа носителя вторичного нечеткого множества: какова область значений входных переменных, для которых носитель вторичного множества разбивается на непересекающиеся интервалы, какова величина промежутка между границами соседних интервалов и т.п..
Метод лишь выявляет «подозрительные» цепочки правил нечеткого логического вывода, в результате которого может быть получен неустойчивый результат (взаимоисключающие прогнозы, взаимоисключающие диагнозы и т.д.) для найденных интервалов входных переменных. Метод подтверждает рекомендации уделять внимание расположению максимумов функций принадлежности крайних термов относительно границ интервалов возможных значений выходной переменной.
Нечеткие логико-лингвистические системы, описываемые наборами значений входных и выходных лингвистических переменных, отношения между которыми задаются эвристическими правилами, могут формально представлять профессиональные тексты. Как в логике, так и в лингвистике под импликацией подразумевается некая причинно-следственная связь, а как имплицитная рассматривается не выраженная в явном виде, подразумеваемая посылка. Чем длиннее цепочка вывода с использованием эвристик, тем дальше следствия находятся от поверхностной, эксплицитной части семантики, тем выше мера нечеткости результирующих суждений как в лингвистической экспертизе текста, так и в нечетких системах управления.
Работа выполнена при поддержке Российского научного фонда (РНФ № 14-11-00432).
Литература
- Flouris G., Huang Z., Pan J.Z., Plexousakis D., and Wache H. Inconsistencies, Negations and Changes in Ontologies [Текст]// Proceedings of the 21st National Conference on Artificial Intelligence (AAI-06). - 2006. - P. 1295-1300. [Электронный ресурс] - Режим доступа. - URL: http://users.ics.forth.gr/~fgeo/Publications/AAAI06.pdf
- Баранов А.Н. Скрытое (имплицитное) утверждение в лингвистической экспертизе текста // Труды первой Интернет-конференции «Право как дискурс, текст и слово», 2010. [Электронный ресурс] - Режим доступа. - URL: http://siberia-expert.com/publ/konferencii/konferencija_2010/9-1-0-325
- Казаченко О.В. Когерентность и когезия текста. Московский институт лингвистики. Альманах современной науки и образования. Тамбов: Грамота, 2009. № 8. Ч. 2. С. 88-90. [Электронный ресурс] - Режим доступа. - URL: http://www.gramota.net/materials/1/2009/8-2/37.html
- Козаченко Н.П. Критерии рациональности изменения убеждений: Непротиворечивость // Логические исследования. Ежегодник Института философии РАН. - 2010. - Вып. 16. - С. 134-155. [электронный ресурс] - Режим доступа. - URL: http://iph.ras.ru/uplfile/logic/log16/LI-16kozachenko.pdf
- Корниенко Е.А. К вопросу об импликации в профессиональном тексте. [электронный ресурс] - Режим доступа. - URL: http://pglu.ru/upload/iblock/c2f/uch_2009_iii_00017.pdf
- Поспелов И.Г., Поспелова Л.Я. Динамическое описание систем продукций и проверка непротиворечивости продукционных экспертных систем // Изв. АН СССР. Техническая кибернетика. - 1987. - № 1. - С. 184-192.
- Поспелова Л.Я. Метод автоматического выявления несогласованностей в статических нечетких системах продукций // Международный научный институт “Educatio”: ежемесячный научный журнал. Часть 2. Технические науки. 2015. № 2(9). С. 134-139. [электронный ресурс] - Режим доступа. - URL: http://cyberleninka.ru/article/n/metod-avtomaticheskogo-vyyavleniya-nesoglasovannostey-v-staticheskih-nechetkih-sistemah-produktsiy
- Савчук В.В. Что такое повороты в философии? // Доклад на историко-методологическом семинаре “Русская мысль”. РХГА. 2012. С. 2-14. [электронный ресурс] - Режим доступа. - URL: http://rhga.ru/science/conferences/rusm/stenogramms/savchuk.php
References
- Flouris G., Huang Z., Pan J.Z., Plexousakis D., and Wache H. Inconsistencies, Negations and Changes in Ontologies [Text] // Proceedings of the 21st National Conference on Artificial Intelligence (AAI-06). - 2006. - P. 1295-1300. - [Electronic resource] – access Mode - URL: http://users.ics.forth.gr/~fgeo/Publications/AAAI06.pdf
- Baranov A.N. Skrytoe (implicitnoe) utverzhdenie v lingvisticheskoj jekspertize teksta [The hidden (implicit) statement in linguistic examination of the text] // Trudy pervoj Internet-konferencii «Pravo kak diskurs, tekst i slovo» [Works of the first Internet conference "Right as Discourse, Text and Word"]. – 2010. - [Electronic resource] – access Mode - URL: http://siberia-expert.com/publ/konferencii/konferencija_2010/9-1-0-325 [in Russian]
- Kazachenko O.V. Kogerentnost' i kogezija teksta. Moskovskij institut lingvistiki. Al'manah sovremennoj nauki i obrazovanija. [Coherence and cohesion of the text. Moscow institute of linguistics. Almanac of modern science and education] [Text] – Tambov: Gramota, 2009. – № 8. – Ch. 2. – P. 88–90. - [Electronic resource] - access Mode - URL: http://www.gramota.net/materials/1/2009/8-2/37.html [in Russian]
- Kozachenko N. P. Kriterii racional'nosti izmenenija ubezhdenij: Neprotivorechivost' [Criteria of rationality of change of beliefs: Consistency] [Text] // Logicheskie issledovanija. Ezhegodnik Instituta filosofii RAN [Logical researches. Year-book of Institute of philosophy of RAS] – 2010. – Issue 16. – Page 134-155. - [Electronic resource] - access Mode - URL: http://iph.ras.ru/uplfile/logic/log16/LI-16kozachenko.pdf [in Russian]
- Korniyenko E. A. K voprosu ob implikacii v professional'nom tekste [To a question of implication in the professional text]. - [Electronic resource] – access Mode - URL: http://pglu.ru/upload/iblock/c2f/uch_2009_iii_00017.pdf [in Russian]
- Pospelov I. G., Pospelova L. Ya. Dinamicheskoe opisanie sistem produkcij i proverka neprotivorechivosti produkcionnyh jekspertnyh sistem [Dynamic description of production systems and check of consistency of productional expert systems] [Text] // Izv. AN SSSR. Tehnicheskaja kibernetika. [Izv. Academy of Sciences of the USSR. Technical cybernetics]. - 1987. - No. 1. - P. 184-192. [in Russian]
- Pospelova L. Metod avtomaticheskogo vyjavlenija nesoglasovannostej v staticheskih nechetkih sistemah produkcij [A method of automatic detection of inconsistencies in the static fuzzy production systems] [Text] // Mezhdunarodnyj nauchnyj institut “Educatio”: ezhemesjachnyj nauchnyj zhurnal. Chast' 2. Tehnicheskie nauki. [International scientific institute "Educatio": monthly scientific magazine. Part 2. Technical science.]. - 2015. - № 2(9). С. 134-139. - [Electronic resource] - access Mode - URL: http://cyberleninka.ru/article/n/metod-avtomaticheskogo-vyyavleniya-nesoglasovannostey-v-staticheskih-nechetkih-sistemah-produktsiy [in Russian]
- Savchuk V. V. Chto takoe povoroty v filosofii? [What is turns in philosophy?] // Doklad na istoriko-metodologicheskom seminare “Russkaja mysl'”. RHGA. [The report at a historical and methodological seminar "The Russian thought". RHGA] - 2012. - С. 2-14. - [Electronic resource] - access Mode - URL: http://rhga.ru/science/conferences/rusm/stenogramms/savchuk.php [in Russian]
