Our journals
Submit manuscript Sign in / Sign up
Advanced search
Article sections

ALGORITHM FOR FINITE ELEMENT MESH GENERATION USING TRIANGULAR SUBDIVISION SCHEMES

Research article
Berzin D.V.
DOI:
https://doi.org/10.18454/IRJ.2015.41.042
Issue: № 10 (41), 2015
Published:
2015/16/11
PDF

Берзин Д.В.

Кандидат физико-математических наук, доцент,

Финансовый университет при Правительстве Российской Федерации, Москва

АЛГОРИТМ ПОСТРОЕНИЯ СЕТИ МЕТОДОМ ТРЕУГОЛЬНЫХ ПОДРАЗБИЕНИЙ

Аннотация

В данной работе описан алгоритм построения треугольной сети для заданной посредством контрольных точек поверхности NURBS. Используются два метода подразбиений –  Loop и Modified Butterfly.

Ключевые слова: информационные технологии, NURBS, треугольная сеть,  алгоритм подразбиения, геометрическое моделирование, прикладная информатика.  

Berzin D.V.

PhD,  Associate Professor,

 Financial University under the Government of the Russian Federation, Moscow

ALGORITHM FOR FINITE ELEMENT MESH GENERATION USING TRIANGULAR SUBDIVISION SCHEMES

Abstract

We suggest here a new algorithm for triangular finite element mesh generation for NURBS surface represented as a set of control points. We use a modern approach – subdivision techniques, which has many advantages. Two different subdivision schemes are presented here: Modified Butterfly and Loop ones.

Keywords: Information Technology, NURBS, Finite element mesh, subdivision algorithm, geometric modeling, applied informatics.  
  1. Формулировка проблемы

Рассмотрим двумерную поверхность S, заданную посредством контрольных точек, см. [1]. Таким образом, в нашем распоряжении имеется множество контрольных точек, веса, последовательность узлов 05-11-2015 11-22-21i= -1, … , L+1; j=-1, … , M+1; n=0, …, L; k=0, … , M. И соответствующая поверхность NURBS представлена в следующей параметрической форме:

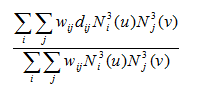
05-11-2015 11-22-35

В системах CAD, треугольные подразбиения имеют определенные преимущества перед прямоугольными [1]. К примеру, они не подвержены определенным видам вырожденности и лучше подходят для описания сложных геометрических объектов.

Нашей целью является построение треугольной сети отвечающей следующим условиям [2,3]. Треугольники должны удовлетворять определенному соотношению сторон, проще говоря, они должны быть максимально близки к правильным треугольникам. Вершины треугольников должны принадлежать данной поверхности S. Расстояние d между треугольником и поверхностью должно быть меньше предписанного (пользователем) числа. Кроме того, пользователь должен иметь возможность адаптивно менять сеть (например, плотность сети в определенных областях).

 
  1. Решение проблемы
Без потери общности, будем рассматривать поверхность S, заданную в виде бикубического B-сплайна.

Шаг 1.  Трансформируем данный бикубический B-сплайн в бикубическую форму Bezier. Это является стандартной процедурой в CAGD ([1]), и она может быть реализована подпрограммой, скажем, “Bezier”. Предположим,  теперь у нас есть прямоугольная сеть точек 05-11-2015 11-33-01 , и все они принадлежат S (см. [6]) . Рассмотрим прямоугольную область R , натянутую на точки A , что имеет место гомеоморфизм

g: R→S,  05-11-2015 11-23-23. Вообще говоря, мы можем рассмотреть многогранник P вместо прямоугольника R, где 05-11-2015 11-26-15([3]).

Шаг 2. Чтобы построить начальную сеть, мы выбираем точки из множества 05-11-2015 11-26-34. Мы хотим, чтобы начальная сеть удовлетворяла требованию соотношения сторон (aspect ratio). Подпрограмма, скажем, “Initial” использует технику диагонального транспонирования [3]: она рассматривает прямоугольник 05-11-2015 11-27-18, сравнивает 05-11-2015 11-27-34и 05-11-2015 11-27-52, и выбирает кратчайшую диагональ, чтобы разбить прямоугольник на два треугольника.

Шаг 3a. Для процесса подразбиения, мы предлагаем интерполяционную Modified Butterfly схему ([4]). Она является С1-непрерывной на регулярных сетях. В отличие от аппроксимирующих схем, основанных на сплайнах, она не дает кусочно-полиномиальной поверхности в пределе. Мы можем предполагать, что поверхности подразбиений 05-11-2015 11-28-43(R) приближаются к заданной поверхности S. Здесь 05-11-2015 11-28-43 → f , и f (R)  является поверхностью подразбиения. После четвертого шага подразбиения, мы получаем соответствующую треугольную сеть (см. [7]).

Пользователь может интерактивно менять уровень подразбиения в различных областях. Эту подпрограмму мы назвали “Subdivision”.

Шаг 3b. Вместо Modified Butterfly схемы, иногда выгоднее использовать другие треугольные схемы. Одной из наиболее популярных схем является аппроксимирующая Loop схема [4]. В сущности, это простейшая схема вставки вершин в треугольные сети, предложенная Чарльзом Лупом. Схема основана на так называемом трехнаправленном коробчатом сплайне, она генерирует C2-непрерывные поверхности на регулярных сетях. В общем же случае, Loop схема генерирует поверхности, которые C2-непрерывны всюду, за исключением особых вершин, где они являются  C1-непрерывными. Схема может быть применена к произвольным "многоугольным" сетям, т.е. состоящим из многоугольников. "Многоугольная" сеть преобразуется в треугольную, к примеру, посредством триангуляции каждой многоугольной грани. Программа подразбиений была написана моим коллегой Никитой Кожекиным на Microsoft Visual C++, используя MFC (Microsoft Foundation Classes) технологию, OpenGL и VTK (свободно-распространяемый инструмент визуализации).

Шаг 4. После k-того уровня подразбиений мы проектируем (посредством подпрограммы “Projection”) сеть на поверхность S.

Шаг 5. Теперь мы проверяем условие, что соответствующие треугольники плотно прилегают к поверхности S, для чего измеряем расстояние от барицентра треугольника до поверхности. Назовем эту подпрограмму “Distance”. Чтобы сеть соответствовала предъявляемым к ней требованиям, мы можем использовать метод [5] для разбиения больших треугольников в несколько меньших по размеру.

Литература

  1. Gerald Farin “Curves and surfaces for CAGD” // Academic press, 1993.
  2. Ho-Le K. “Finite element mesh generation methods: review and classification” // Computer-Aided Design, 20:27-38, 1988
  3. K.-J. Bathe “Finite Element Procedures” // Prentice-Hall, 1996
  4. “Subdivision for Modeling and Animation” // SIGGRAPH 99 Course Notes.
  5. Rivara M.C. “Algorithms for refining triangular grids suitable for adaptive and multi-grid techniques” // Int. J. Numer. Meth. Eng. Vol 20 (1984) pp. 745-756.
  6. Dmitry Berzin "Finite element mesh generation using subdivision technique" // Международный научно-исследовательский журнал = Research Journal of International Studies, №8 (27) 2014, p. 6
  7. Dmitry Berzin "Finite element automatic mesh generation using Modified Butterfly subdivision scheme" // Международный научно-исследовательский журнал = Research Journal of International Studies, №8 (27) 2014, p. 8
  8. Dmitry Berzin "Finite element mesh automatic generation using triangilar subdivision schemes" // Международный научно-исследовательский журнал = Research Journal of International Studies, №9 (28) 2014, p. 5

References

  1. Gerald Farin “Curves and surfaces for CAGD” // Academic press, 1993.
  2. Ho-Le K. “Finite element mesh generation methods: review and classification” // Computer-Aided Design, 20:27-38, 1988
  3. K.-J. Bathe “Finite Element Procedures” // Prentice-Hall, 1996
  4. “Subdivision for Modeling and Animation” // SIGGRAPH 99 Course Notes.
  5. Rivara M.C. “Algorithms for refining triangular grids suitable for adaptive and multi-grid techniques” // Int. J. Numer. Meth. Eng. Vol 20 (1984) pp. 745-756.
  6. Dmitry Berzin "Finite element mesh generation using subdivision technique" // Research Journal of International Studies, №8 (27) 2014, p. 6
  7. Dmitry Berzin "Finite element automatic mesh generation using Modified Butterfly subdivision scheme" // Research Journal of International Studies, №8 (27) 2014, p. 8
  8. Dmitry Berzin "Finite element mesh automatic generation using triangilar subdivision schemes" // Research Journal of International Studies, №9 (28) 2014, p. 5