Computer simulation of plutonium dioxide crystallisation from fusion
Computer simulation of plutonium dioxide crystallisation from fusion
Abstract
Molecular dynamics simulation of the crystallisation of nanoscale molten PuO2 droplets isolated in a vacuum was performed. It was shown that the crystallisation process began at the surface. Once formed, the crystalline phase spread into the volume in a time of about 0.2 ns. At a given temperature, an increase in the size of the model system led to a decrease in the average time from the start of the computational experiment to the onset of crystallisation. The time to the onset of crystallisation was a random variable, and crystallisation could be regarded as a thermally activated process. Theoretical estimates of the low-temperature limit of the existence of metastable PuO2 liquid droplets were obtained using a surface liquid model.
1. Введение
Известно, что температуры плавления и кристаллизации наночастиц могут быть снижены на сотни градусов по сравнению с макроскопическими системами. Этот эффект был экспериментально зафиксирован, в том числе для кристаллов диоксида урана, используемых в качестве оксидного ядерного топлива . Локальное плавление и рекристаллизация решетки ядерного топлива могут происходить в окрестности термических всплесков (thermal spikes), создаваемых быстрыми частицами. Эти процессы могут влиять на формирование структуры глубокого выгорания, при образовании которой средний размер зерна понижается до значений 100 – 300 нм .
Существуют работы, в которых методом молекулярной динамики успешно моделировали понижение температуры плавления нанокристаллов UO2 , . Представляет интерес вычислительное моделирование обратного процесса — кристаллизации расплавленных наноразмерных капель, поскольку механизм кристаллизации может не совпадать с плавлением, обращенным во времени. В работе исследовали кристаллизацию расплавленных капель PuO2, содержавших от 105 до 174 частиц. Температура кристаллизации составила 1700 K, что на 1300 K ниже экспериментальной оценки температуры плавления макроскопического PuO2. Однако при рассмотрении столь малых систем не было возможности разделить процессы, связанные с поверхностью и с объёмом. В настоящей работе размер модельных систем увеличен до 27600 частиц.
2. Методика молекулярно-динамического моделирования
Модельными системами в настоящей работе были наноразмерные сферические капли расплавленного PuO2, изолированные в вакууме. Капли состояли из 5460, 15960 и 27600 частиц. Взаимодействия ионов плутония и кислорода описывали парными потенциалами MOX-07, предложенными в работе . Ранее эти потенциалы позволили получить хорошие результаты при моделировании дефектообразования, диффузии собственных ионов, распространения трещин , , . Уравнения движения интегрировали методом «с перешагиванием» и шагом Dt = 3×10-15 c. Для стабилизации температуры использовали термостат Берендсена . Высокую производительность моделирования обеспечивали распараллеливанием вычислений на графических процессорах архитектуры CUDA, с применением оригинального программного комплекса.
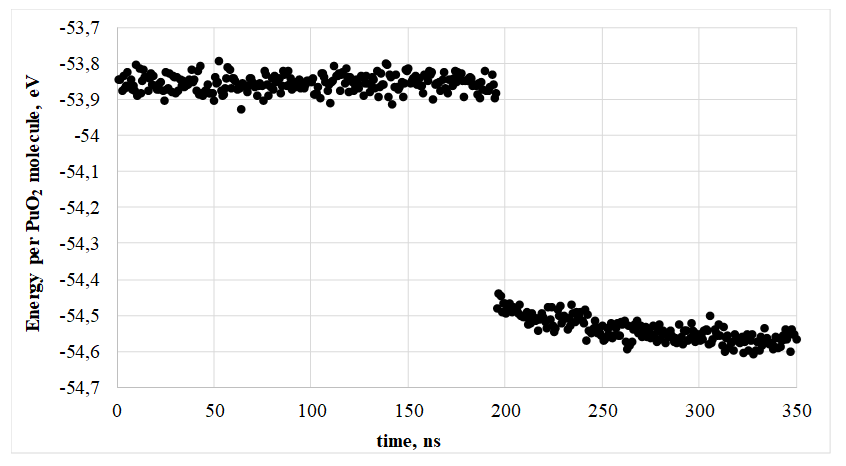
Рисунок 1 - Удельное изменение энергии при кристаллизации, T = 2525 К, 15960 частиц
3. Обсуждение результатов
Как видно из Рисунка 1, кристаллизация при моделировании была термически активируемым процессом. Время существования расплавленной капли до кристаллизации при одной и той же температуре могло различаться на порядок величины. Время кристаллизации в настоящей работе рассматривали как случайную величину с плотностью распределения
Здесь n — частота событий кристаллизации, зависящая от температуры и высоты потенциального барьера E(T). Среднее значение времени начала кристаллизации при такой плотности распределения даётся формулой (2):
Рисунком 2 проиллюстрирована начальная стадия процесса кристаллизации расплавленной «капли». Упорядоченные кристаллические плоскости формировались на поверхности «капли», после чего периодическая структура постепенно занимала всю систему, распространяясь с одной стороны (сверху вниз на Рисунке 2). Кристаллическая фаза распространялась в объем за время порядка 0.2 нс.
На Рисунке 3 приведены графики зависимости среднего времени кристаллизации модельных систем от температуры для различных размеров (5460, 15960 и 27600 частиц). Видно, что среднее время от старта вычислительного эксперимента до начала кристаллизации при равных температурах и меньших систем выше, чем у расплавленных капель большего размера. Объяснить указанный эффект можно тем, что вероятность образования зародыша кристаллической фазы на единице поверхности независима от размеров системы. Тогда чем больше площадь поверхности «капли», тем выше вероятность образования кристаллической фазы в единицу времени.

Рисунок 2 - Начало процесса кристаллизации: 27600 частиц, Т = 2525 К
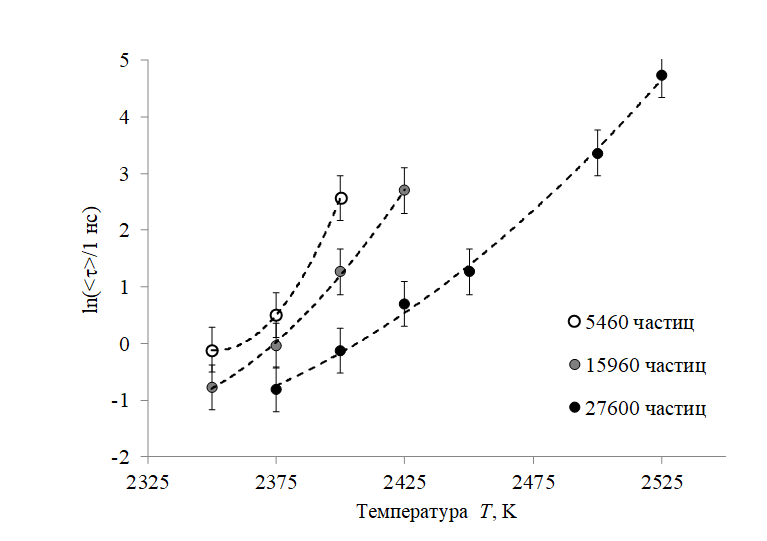
Рисунок 3 - Среднее время кристаллизации модельных систем
где L — скрытая теплота плавления, приходящаяся на одну молекулу; NL — количество молекул в расплавленном слое; AC, AL, AS — площади поверхности кристаллического ядра, расплавленного слоя и твердого кристалла (NL = 0), соответственно; γSL, γLM, γSM — удельные энергии Гельмгольца на границах между твердым (S), жидким (L) слоями и матрицей среды M (внешней средой в настоящей работе был вакуум); T — температура термостата, Tmb — температура плавления кристалла бесконечных размеров.
В рамках модели LNG поверхностные энергии γSL и γLM учитывают влияние частичного упорядочения расплавленного слоя под воздействием границ. Глубина проникновения эффекта упорядочивания в жидкость определяется параметром ξL, который в настоящей работе был принят равным постоянной решетки модельных кристаллитов PuO2 вблизи точки плавления: ξL = 0.556 нм.
Здесь Δγ = γSM − (γSL + γLM); nL и VL — молекулярная плотность и объем жидкого слоя. Параметром α Î [0,1] определяется вклад внешней и внутренней поверхностей расплавленного слоя в его свободную энергию.
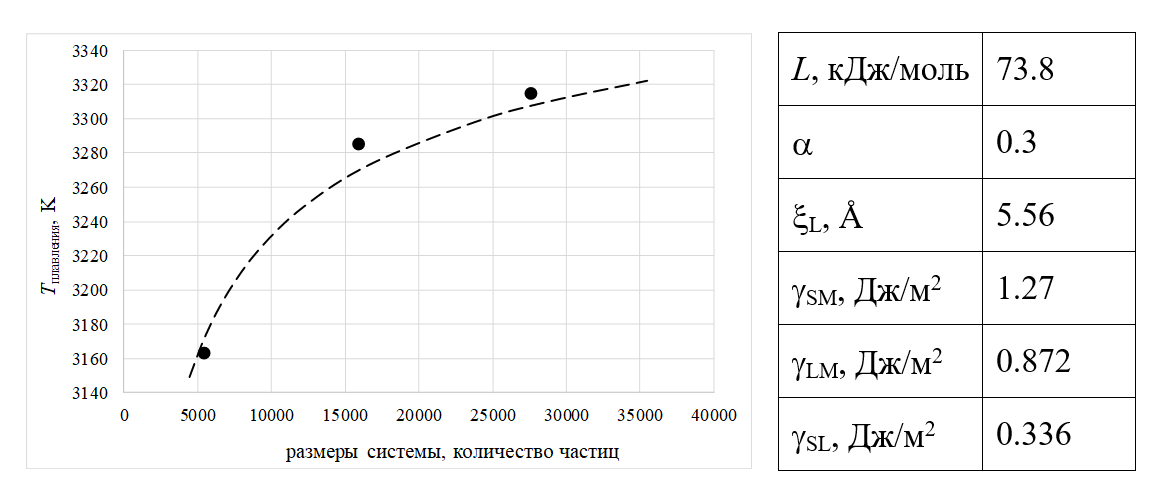
Рисунок 4 - Температуры плавления, прогнозируемые с использованием модели LNG
4. Заключение
Моделирование показало, что кристаллизация наноразмерных капель PuO2 начиналась с поверхности. При заданной температуре увеличение размера модельной системы приводило к уменьшению среднего времени от начала вычислительного эксперимента до начала кристаллизации. Кристаллизацию можно было рассматривать как термически активируемый процесс. Модель нуклеации и роста жидкой оболочки (LNG) позволила получить следующие оценки минимальной температуры существования метастабильного расплава: 2750 K для 27600 частиц, 2620 K для 15960 частиц и 2260 K для 5460 частиц. Первые два значения завышены по сравнению с данными молекулярно-динамического моделирования, проведенного в настоящей работе. Можно предположить, что при низких температурах модельные расплавленные «капли» были неравновесными, однако их кристаллизация всё же не могла происходить без образования зародыша твердой фазы на поверхности расплава.
Можно предположить, что при низких температурах модельные расплавленные «капли» были неравновесными, однако их кристаллизация всё же не могла происходить без образования зародыша твердой фазы на поверхности расплава.
