Journals
Submit manuscript Sign in / Sign up
Advanced search
Article sections
Review

Concentration dependencies of electrical resistance of ternary and binary alloys at maximum long-range order

Research article
Borodin K. I.
Volkov V. A.
DOI:
https://doi.org/10.60797/IRJ.2025.160s.40
Issue: № 10 (160) S, 2025
Suggested:
27.08.2025
Accepted:
28.08.2025
Published:
24.10.2025
183
1
XML
PDF

Abstract

Electrical resistance of ternary and binary alloys was calculated in the coherent potential approximation. Concentration dependencies of electrical resistance at the maximum long-range order for a given composition were studied. The results are presented in graphical form. A comparison with the weak scattering limit has been made. For isoelectronic ternary alloys, it has been established that at low values of the valence electron number, the Fermi level is located quite far from the gap in the electron density of states that emerges with an increase in the concentration of the third component. In this case, the graphs of the dependence of the residual electrical resistance on the concentration of the third component, obtained in the coherent potential approximation (CPA) and in the weak scattering approximation (WSA), are qualitatively similar. With an increase in the number of valence electrons, the concentration dependencies of the resistance for CPA and WSA acquire qualitative differences.

Keywords:
residual resistivity ratio, ternary and binary alloys, maximum order, coherent potential approximation.

1. Введение

Упорядочивающиеся сплавы играют исключительно важную роль в современной науке и технике. Возможность варьирования физических свойств за счет изменения состава и внутренней структуры делает их незаменимыми в качестве конструкционных материалов, широко используемых в различных отраслях промышленности.

Многие приложения упорядочивающихся сплавов обусловлены их уникальными резистивными характеристиками. Однако, следует отметить, что если температурные зависимости электросопротивления 

 таких сплавов исследовались во многих работах, то концентрационным аномалиям 
 уделялось значительно меньше внимания. Приближение когерентного потенциала (ПКП) широко используется в теории сплавов. Так, бинарные неупорядоченные сплавы и их остаточное электросопротивление изучались в ПКП в работах
,
, упорядочение в бинарных сплавах рассматривалось в
, сопротивление бинарных упорядочивающихся сплавов исследовалось в
,
,
,
, тройные сплавы анализировались в 
,
.

Целью данной работы является теоретический расчет концентрационных зависимостей электросопротивления тройных и бинарных упорядочивающихся сплавов в ПКП при максимально возможном для данной концентрации дальнем порядке.

2. Остаточное электросопротивление тройных и бинарных упорядочивающихся сплавов

Пусть 

 концентрации компонент сплава, имеющего ОЦК-решетку с двумя типами узлов. Упорядочение в такой системе можно описать двумя параметрами дальнего порядка 

(1)

где 

 — вероятность заполнения узлов 
-й подрешетки атомами сорта 
 
.

Интересующие нас физические характеристики сплава могут быть выражены через когерентные потенциалы подрешеток 

, которые определяются из условия равенства нулю усредненных по конфигурациям t- матриц рассеяния неэквивалентных узлов

(2)

Здесь 

(3)

- t — матрица рассеяния узла 

-й подрешетки, занятого атомом сорта 
l$$\alpha, \varepsilon_\alpha
 — энергия атомного уровня для узла, оккупированного атомом сорта 
, 

(4)
(5)
(6)

 — плотность электронных состояний, соответствующая чистому металлу 
 в случае 
. Далее функция 
 будет аппроксимироваться полуэллиптической кривой, полуширина которой равна единице
. Тогда 

(7)

 и система уравнений (2) может быть записана в эквивалентном виде

(8)

Плотность электронных состояний упорядочивающегося сплава выражается через решения системы (8) следующим образом

(9)

а статическая проводимость 

 запишется как 

(10)

Здесь 

 — заряд электрона, 
 — объем, приходящийся на один атом, 
 — максимальная скорость в полосе, 
 — энергия Ферми сплава, которая может быть найдена из соотношения

(11)

где 

 — число валентных электронов компонента 
; объем зоны сплава нормирован на единицу.

Рассмотрим концентрационные зависимости характеристик тройного сплава вдоль квазибинарных разрезов 

\left(\mathrm{c}_\alpha=\right.$ const,$\left.\alpha=\{A, B, C\}\right)
 при максимально возможном для данной концентрации дальнем порядке. Исследуем случай, когда при упорядочении атомы сорта А обладают приоритетом в размещении на узлах первой подрешетки по сравнению с атомами других сортов. При этом атомы сорта С, размещаясь на узлах, незанятых атомами сорта А, могут располагаться преимущественно либо на узлах первой подрешетки (тип упорядочения I), либо на узлах второй подрешетки (тип упорядочения II). Таким образом для тройного сплава с ОЦК-решеткой можно рассматривать шесть различных типов концентрационных зависимостей вдоль квазибинарных разрезов при максимальном порядке.

Экстремальные значения параметров дальнего порядка 

 вычисляются по формулам

\mathrm{c}_A=$ const $\leq \frac{1}{2}\left\{\begin{array}{c}\eta_e=2 \mathrm{c}_A \\ \xi_{e I}=\left[\begin{array}{c}2{ }^c{ }_C, 0 \leq{ }_C \leq \frac{1}{2}-{ }^c{ }_A \\ 2\left(1-2{ }^c{ }_A-{ }^c C\right), \frac{1}{2}-{ }^c{ }_A \leq{ }_C \leq 1-{ }_C A\end{array}\right. \\ \xi_{e I I}=\left[\begin{array}{c}-2{ }_C, 0 \leq{ }_C \leq \frac{1}{2}, \\ -2\left(1-{ }_C\right), \frac{1}{2} \leq{ }_C \leq 1-{ }_C{ }_A\end{array}\right.\end{array}\right.
(12)
c_B=$ const $\leq \frac{1}{2}\left[\begin{array}{c}\eta_e=\left[\begin{array}{c}2 c_A, 0 \leq c_A \leq \frac{1}{2}, \\ 2\left(1-c_A\right), \frac{1}{2} \leq c_A \leq 1-c_B, \\ \xi_{e I}=\left[\begin{array}{c}2\left(c_B-c_A\right), 0 \leq c_A \leq \frac{1}{2}, \\ -2\left(1-c_B-c_A\right), \frac{1}{2} \leq c_A \leq 1-c_B,\end{array}\right. \\ \xi_{e I I}=\left[\begin{array}{c}-2\left(c_A+c_B\right), 0 \leq c_A \leq \frac{1}{2}-c_B, \\ -2\left(1-c_B-c_A\right), \frac{1}{2}-c_B \leq c_A \leq 1-c_B\end{array}\right.\end{array}\right.\end{array}\right.
(13)
c_C=$ const $\leq \frac{1}{2}\left[\begin{array}{c}\eta_e=\left[\begin{array}{c}2 c_A, 0 \leq c_A \leq \frac{1}{2} \\ 2\left(1-c_A\right), \frac{1}{2} \leq c_A \leq 1-c_C\end{array}\right] \\ \xi_{e I}=\left[\begin{array}{c}2{ }^2 c_C, 0 \leq c_A \leq \frac{1}{2}-c_C \\ 2\left(1-2 c_A-c_C\right), \frac{1}{2}-c_C \leq c_A \leq \frac{1}{2} \\ -2 c_C, \frac{1}{2} \leq c_A \leq 1-c_C \\ \xi_{e I I}=-2 c_C\end{array}\right.\end{array}\right.
(14)

Фиксируя концентрацию одной из компонент и изменяя с некоторым шагом концентрацию другой, вычислим по формулам (12), (13), (14) экстремальные значения параметров дальнего порядка и подставим их в систему уравнений (8).

Далее система уравнений (8) решалась численно на ЭВМ итерационным методом, а затем по формуле (9) вычислялась плотность электронных состояний сплава 

. После этого из соотношения (11) определялась энергия Ферми 
 и находились плотность электронных состояний на уровне Ферми 
 и удельное остаточное электросопротивление сплава 
 (10). Так, были получены концентрационные зависимости энергии Ферми, плотности электронных состояний на уровне Ферми и остаточного электросопротивления тройных сплавов вдоль квазибинарных разрезов при максимальном дальнем порядке.

Рассмотрим бинарный упорядочивающийся сплав ОЦК-решеткой. Основные формулы для такого сплава могут быть легко получены из соответствующих выражений для тройного сплава с ОЦК-решеткой, если мы учтем, что структуры этих систем идентичны, и отличие имеется только в числе компонент. Поэтому если положим 

 и в формулах (2), (8), (11) при суммировании по 
 ограничимся случаем 
, то полученные выражения будут описывать бинарный сплав; при этом соотношения (3) – (7), (9), (10) могут использоваться без каких-либо изменений. Упорядочение в бинарном сплаве с ОЦК-решеткой описывается одним параметром дальнего порядка 
 (1), а его экстремальные значения 
 вычисляются по формуле

(15)

3. Основные результаты и их обсуждение

Насколько нам известно, концентрационные зависимости подобного рода для электросопротивления тройных сплавов экспериментально изучались, как правило, при комнатных температурах. Поэтому результаты выполненных в ПКП расчетов сравним с данными, полученными для сопротивления в пределе слабого рассеяния (ПСР). В этом приближении для немагнитного сплава в случае, когда уровень Ферми расположен вдали от щели, для 

 получим (см. подробнее в
,
)

(16)

где 

 - константа, не зависящая от состава и параметров порядка, 
. 

На рисунках 1 и 2 представлены концентрационные зависимости характеристик тройного сплава вдоль различных квазибинарных разрезов при максимальном порядке. Остаточное сопротивление изображено в единицах 

. Мы исследовали изоэлектронные сплавы, в которых 
. Штрихпунктирной линией изображен график 
 в пределе слабого рассеяния (16). Константа 
 выбиралась такой, чтобы при 
 значения электросопротивления, полученные в ПКП и ПСР, совпадали. В случае, когда максимальный порядок в системе описывается формулой (12) (типы концентрационных зависимостей AI и AII), в плотности электронных состояний сплава при увеличении 
 образуются щели, расположение и число которых зависит от 
 и типа упорядочения. Начиная с 
 приблизительно 0,1-0,2, слева от 
 отделяется подзона, форма которой при увеличении 
 претерпевает изменения, а объем остается практически постоянным и составляет около 30% от объема всей зоны. Поэтому значению 
 соответствует ситуация, когда уровень Ферми расположен довольно далеко от щели, а 
 (т. е. число носителей заряда) изменяется монотонно (Рис. 1а и 2а). В этом случае характер зависимости 
 будет определяться главным образом изменением состава сплава, поскольку при этом изменяется число актов рассеяния с заданной интенсивностью такового. В формуле (16) интенсивность рассеяния электрона проводимости при перескоке от атома 
 к атому 
 задается параметром 
 , а число соответствующих актов рассеяния — множителем при 
, стоящим в квадратных скобках, т. е. составом и упорядоченностью сплава. Так как именно эти факторы (но не число носителей заряда) представлены в выражении (16), описывающем остаточное сопротивление в ПСР, то полученные в ПКП графики 
 при 
 (Рис. 1а и 2а) качественно похожи (по числу и расположению экстремумов) на рассчитанные по (16) кривые 
, хотя, конечно, численные значения их различны, точки максимума несколько сдвинуты и т. д.

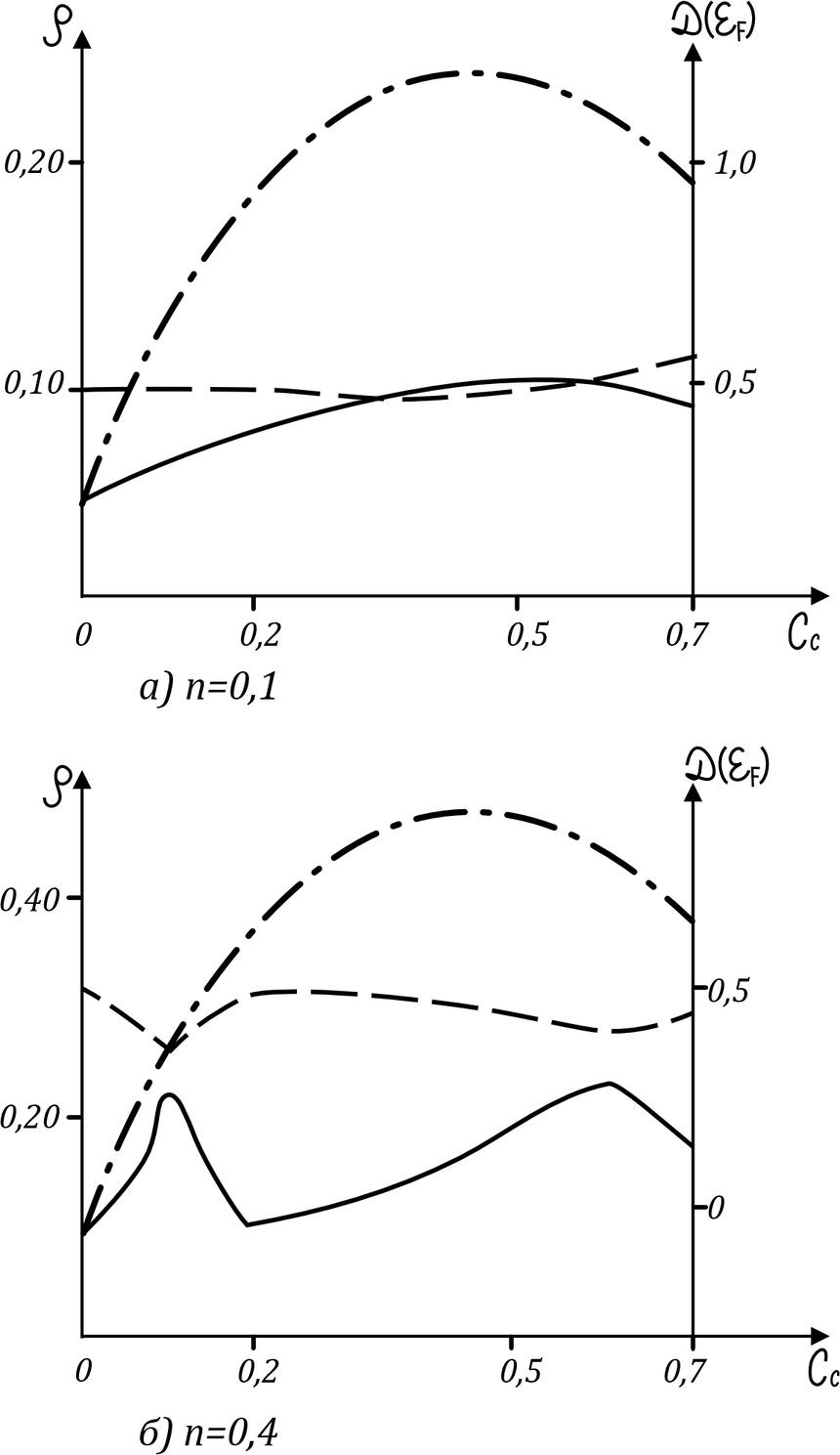
Тройной сплав: концентрационные зависимости плотности электронных состояний на уровне Ферми (штриховая линия) и остаточного электросопротивления (сплошная линия) вдоль квазибинарного разреза при максимальном порядке (тип AI, cA =0,3 = const)

Рисунок 1 - Тройной сплав: концентрационные зависимости плотности электронных состояний на уровне Ферми (штриховая линия) и остаточного электросопротивления (сплошная линия) вдоль квазибинарного разреза при максимальном порядке (тип AI, cA =0,3 = const)

Примечание: здесь εA = -0,5; εB = 0; εC = 0,5

DOI:10.60797/IRJ.2025.160s.40.1

При 

 (Рис. 1б) уровень Ферми попадает в область, где при увеличении 
 происходит значительная перестройка электронной структуры, а 
изменяется немонотонно, что приводит к существенным качественным отличиям полученной в ПКП концентрационной зависимости сопротивления от 
 в пределе слабого рассеяния. В случае концентрационной зависимости CII (14) отделяющаяся слева от 
 подзона при увеличении 
 претерпевает изменения как формы, так и объема. Полное её отделение происходит при 
. Поэтому при 
, хотя уровень Ферми и расположен довольно далеко от щели, 
 изменяется немонотонно, в результате рассчитанная в ПКП концентрационная зависимость сопротивления при максимальном дальнем порядке имеет ряд качественных отличий по сравнению с 
 в ПСР (Рис. 2б).

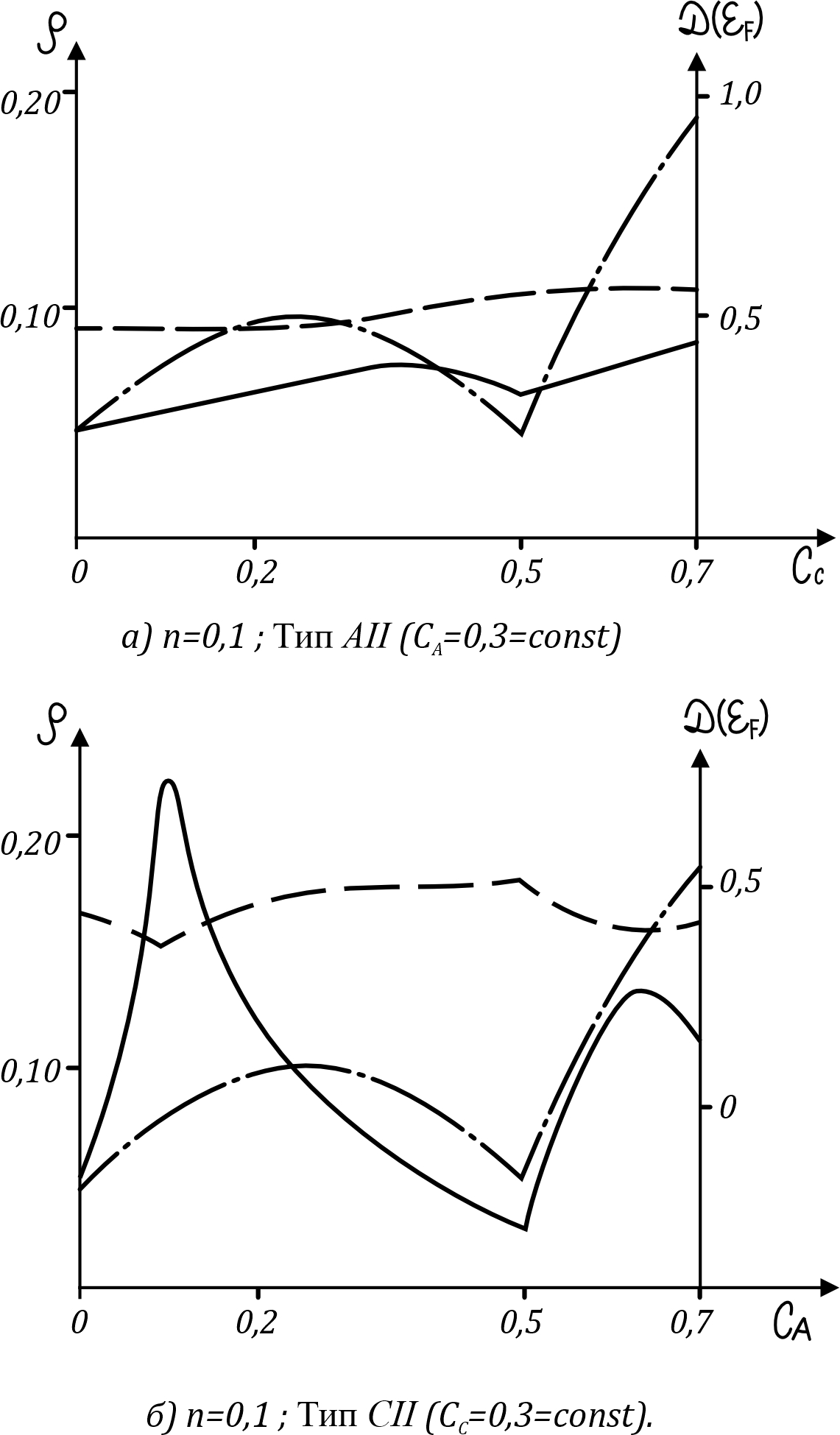
Тройной сплав: концентрационные зависимости плотности электронных состояний на уровне Ферми (штриховая линия) и остаточного электросопротивления (сплошная линия) вдоль квазибинарного разреза при максимальном порядке

Рисунок 2 - Тройной сплав: концентрационные зависимости плотности электронных состояний на уровне Ферми (штриховая линия) и остаточного электросопротивления (сплошная линия) вдоль квазибинарного разреза при максимальном порядке

Примечание: здесь εA = -0,5; εB= 0; εC = 0,5

DOI:10.60797/IRJ.2025.160s.40.2

Можно заключить, что если для сплавов фиксированного состава (зависимости от температуры отжига) изменение плотности электронных состояний на уровне Ферми (числа носителей заряда) полностью предопределяет поведение остаточного сопротивления, то для сплавов переменного состава (концентрационные зависимости) взаимосвязь между 

 и 
 становится более сложной, поскольку в последнем случае на поведение 
 также оказывает влияние изменение числа актов рассеяния с заданной интенсивностью такового.

Выполненные в ПКП расчеты показывают, что именно немонотонное изменение числа носителей заряда обуславливает аномальный характер как концентрационных, так и температурных зависимостей сопротивления. Заметим, что полный, самосогласованный учет этого фактора возможен именно в ПКП.

Для бинарных упорядочивающихся сплавов соответствующий аналог формулы (16) запишется так

(17)

Здесь 

 — константа, не зависящая от состава и степени упорядочения сплава.

На Рис. 3 

 приведены концентрационные зависимости остаточного электросопротивления и плотности электронных состояний на уровне Ферми при максимально возможном для данной концентрации дальнем порядке. Обратимся к Рис. 3б. Пунктиром на нем нанесена зависимость 
 при максимальном порядке, построенная по формуле (17), где мы взяли 
. Сплошная линия на этом рисунке соответствует случаю промежуточного рассеяния с 
, рассчитанная в ПКП. Сопоставление этих двух кривых показывает, что при промежуточном рассеянии зависимость 
 теряет симметрию относительно точки 
, свойственную случаю слабого рассеяния; для 
0<c_A<0,5
 и 
0,5<c_A<1
 также пропадает симметрия относительно центров этих интервалов. 
, так как при данном составе 
, и система становится трансляционно инвариантной. Имеется также корреляция между 
 и 
 (см. Рис. 3а и 3б): чем меньше плотность электронных состояний на уровне Ферми, тем выше сопротивление.

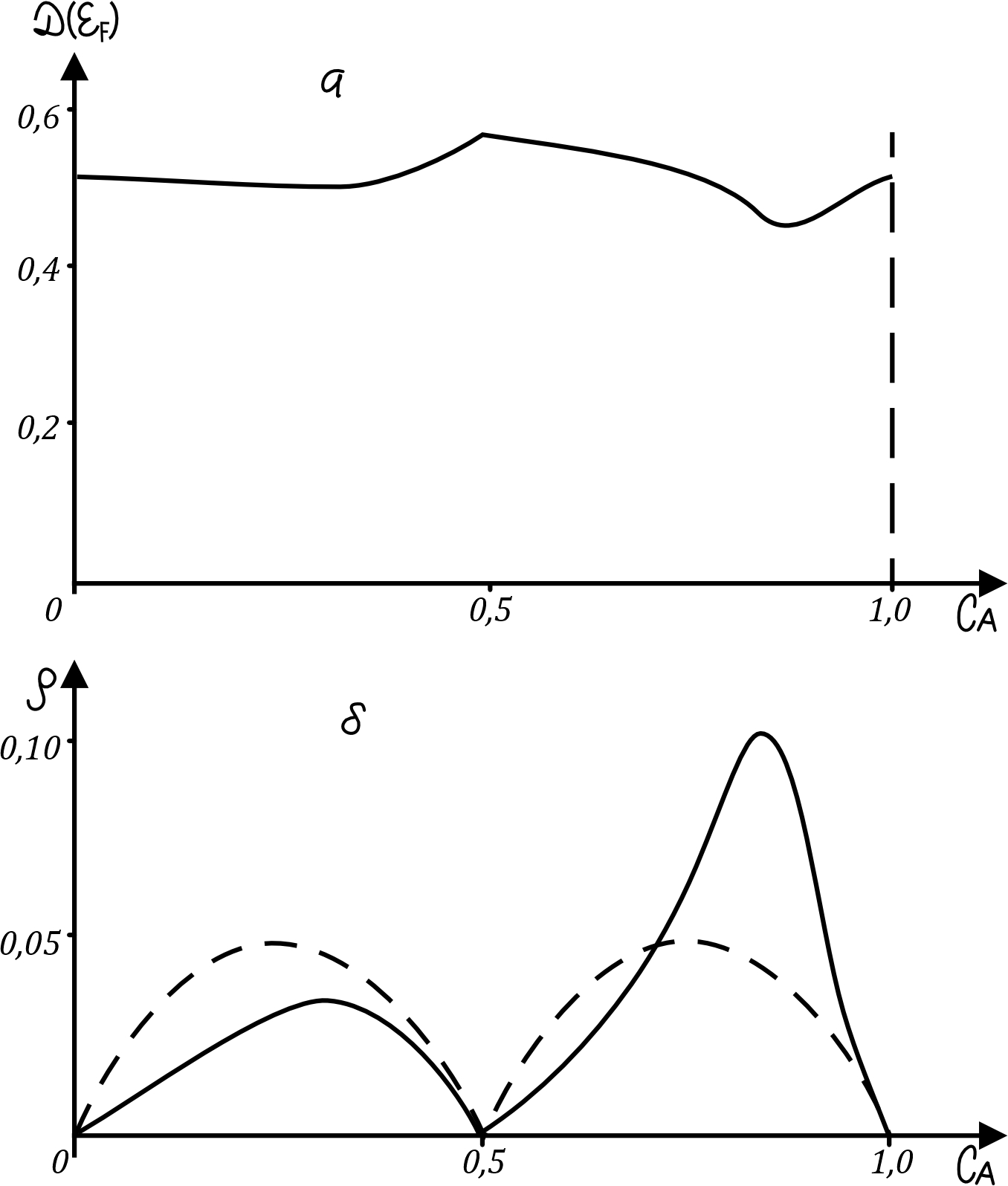
Бинарный сплав: зависимости остаточного электросопротивления и плотности электронных состояний на уровне Ферми от концентрации при максимальном порядке

Рисунок 3 - Бинарный сплав: зависимости остаточного электросопротивления и плотности электронных состояний на уровне Ферми от концентрации при максимальном порядке

DOI:10.60797/IRJ.2025.160s.40.3

4. Заключение

К сожалению, систематические экспериментальные исследования концентрационных зависимостей остаточного электросопротивления тройных сплавов при максимальном дальнем порядке никем не проводились. Поэтому провести детальное сравнение полученных теоретических результатов с экспериментом невозможно. Однако, по нашему мнению, развитая в данной работе теория может служить исходным пунктом и надежным ориентиром при проведении такого экспериментального исследования, необходимость выполнения которого в свете последних технологических применений тройных упорядочивающихся сплавов становится все более очевидной.

Additional materials

Not specified

Financing

Авторы не получали финансовой поддержки для проведения исследования, написания и публикации статьи

Acknowledgements

Not specified

Conflicts of interests

Not specified

References

  • Velicky B.

    Single site approximation in the electronic theory of simple binary alloys
    / B. Velicky, S. Kirkpatrick, H. Ehrenreich //
    Physical Review
    . — 1968. — 3. — P. 747–766.

  • Velicky B.

    Theory of electronic transport in disordered binary alloys coherent potential approximation
    / B. Velicky //
    Physical Review
    . — 1969. — 3. — P. 614–627.

  • Borodachev S.M.

    Ostatochnoe soprotivlenie binarny'x uporyadochivayushhixsya splavov (priblizhenie kogerentnogo potenciala)
    [
    Residual resistance of binary ordered alloys (approximation of coherent potential)
    ] / S.M. Borodachev, V.A. Volkov, S.I. Masharov //
    Fizika metallov i metallovedenie
    [
    Metal Physics and Metal Science
    ]. — 1976. — 6. — P. 1147–1153. [in Russian]

  • Brouers F.

    Order-disorder transition in a model binary alloy
    / F. Brouers, J. Giner, J. Van der Rest //
    J. Phys. F Met. Phys
    . — 1974. — 2. — P. 214–224.

  • Brauvers M.

    Influence of long-range order on electrical resistivity in alloys
    / M. Brauvers, J. Giner, J. Van der Rest et al. //
    Solid State Commun
    . — 1975. — 2. — P. 229–232.

  • Paja A.

    Effect of ordering on the electrical conductivity in binary alloys
    / A. Paja //
    J. Phys. C Solid State Phys
    . — 1976. — 8. — P. 1445–1455.

  • Kudrnovsky J.

    Electrical conductivity of electrons in a model binary disordered alloy with long range order
    / J. Kudrnovsky, B. Velicky //
    Czech. J. Phys
    . — 1977. — 1. — P. 71–87.

  • Volkov V.A.

    E'lektrosoprotivlenie trojny'x uporyadochivayushhixsya ferromagnitny'x splavov
    [
    Electrical resistance of triple ordered ferromagnetic alloys
    ] / V.A. Volkov, A.A. Kuranov, S.I. Masharov et al. //
    Fizika metallov i metallovedenie
    [
    Metal Physics and Metal Science
    ]. — 1979. — 3. — P. 516–523. [in Russian]

  • Wysokinsky K.I.

    Calculation of the DC electrical conductivity of the disordered ternary alloys
    / K.I. Wysokinsky, M. Pilat //
    J. Phys. C Solid State Phys
    . — 1976. — 23. — P. 4271–4279.

  • Krivoglaz M.A.

    Teoriya uporyadochivayushhixsya splavov
    [
    Theory of ordered alloys
    ] / M.A. Krivoglaz, A.A. Smirnov. — Moskva: GIFML, 1958. — 388 p. [in Russian]

Review

All articles are peer-reviewed. But the reviewer or the author of the article chose not to publish a review of this article in the public domain. The review can be provided to the competent authorities upon request.

Author information

AffiliationM. N. Mikheev Institute of Metal Physics, Ural Branch of the Russian Academy of Sciences, Ekaterinburg, Russian Federation
Role:Author, Data curation, Software, Approbation, Visualization, Writing, reviewing and editing, Analysis, Project administrator
ORCID:0000-0001-5536-4256
AffiliationUral Federal University, Ekaterinburg, Russian Federation
Role:Author, Conceptualization, Methodology, Management, Writing, reviewing and editing, Draft writing and preparation, Research data analysis, Analysis
ORCID:0000-0002-7955-959X

Article metrics

Views:183
Downloads:1
Views
Total:
Views:183