Experimental study of hydrodynamics in a cold model of a conical reactor for sawdust gasification using random process theory
Experimental study of hydrodynamics in a cold model of a conical reactor for sawdust gasification using random process theory
Abstract
During the work, a flat cold model of a gas generator was studied, including an air inlet area, a conical section with an opening angle of 38°, a rectangular section measuring 500×20 mm, and an outlet connected to a filter. The unit is equipped with a video surveillance system for dispersed flow and pressure sensors, with digital recording for subsequent statistical analysis. The experiments were carried out with different sawdust fractions (0.1–0.25 mm; 0.25–0.5 mm; 0.5–0.8 mm; 0.8–1.0 mm; 1.0–1.25 mm; 1.25–1.6 mm) and their mixtures, with an initial layer height of 50 mm. The air velocity at the inlet varied from 0.4 to 5.4 m/s, with each experiment lasting 40 seconds. The results showed that at low velocities (0.4–1.9 m/s), the material is in a stable flowing mode with main pressure pulsation frequencies of 3–5 Hz. An increase in speed leads to a transition to unstable pseudo-fluidisation: the fluctuations range expands to 0.5–8 Hz, and at even higher air flow rates, the layer transitions to a rarefied mode with a predominance of low frequencies (about 2 Hz). Smaller fractions (0.1–0.8 mm) lose stability more quickly, while larger particles (0.8–1.6 mm) remain stable for longer. Spectral analysis of pressure pulsations at heights of 30 and 200 mm shows a noticeable change in the root-mean-square deviation of fluctuations in height, with the upper level reacting more strongly to an increase in speed. According to the distribution of static pressure by height, it has been established that the volume concentration of particles in the zone 30–50 mm above the grid reaches 30%. With a further increase in air flow, the layer is washed upward, particle clusters form in areas distant from the diffuser inlet, and the volumetric concentration of particles decreases significantly. The obtained results allow to predict the dynamic behaviour of beds of different dispersibility and contribute to the development of effective gasification processes.
1. Введение
Для получения синтез-газа из древесного опила в реакционной камере газификатора необходимо создавать гидродинамические режимы течения двухфазной среды, обеспечивающие равномерное безагломерационное распределение твердых частиц по объему камеры , и достаточное время пребывания в ней всего полидисперсного состава частиц.
Для контроля гидродинамического режима аппаратов с газодисперсными средами широко применяют амплитудно-частотные характеристики сигнала давления. Liu и соавторы показали, что в установках с фонтанирующим слоем с плотными частицами возможны различные доминирующие частоты фонтанирования (одна, две или несколько). Их появление зависит от соотношения скорости газа к минимальной скорости фонтанирования. При этом диапазон газовых скоростей, в котором сохраняется устойчивая работа, возрастает с увеличением плотности частиц. Анализ колебаний давления позволил разделить разные режимы на карте, включая переходные зоны с двойной или множественной доминирующей частотой. Gryczka и др. исследовали поведение нового фонтанирующего слоя с двумя регулируемыми газовыми входами, используя амплитудно-частотные характеристики. Для определения границ стабильного фонтанирования использовались быстрое преобразование Фурье и измерения полей скорости методом PIV. Переходы к режимам каналообразования или поршневания сопровождались возрастанием амплитуды сигнала и размыванием амплитудно-частотного спектра. Стабильное фонтанирование характеризовалось ровными частотными спектрами и согласованным циркулированием частиц без мёртвых зон. Salikov и соавторы в своей работе уделили особое внимание анализу амплитудно-частотных характеристик сигнала давления для определения устойчивости фонтанирующего слоя. Исследования показали, что при переходе к неустойчивым режимам фонтанирования, связанным с периодическим отклонением фонтана и поршневанием, в спектре сигнала давления появляются новые частоты, а общая энергия колебаний (амплитуда) возрастает. Авторы выявили, что изменение интенсивности пульсаций давления на разных уровнях слоя позволяет разделять устойчивое и переходное состояния, давая количественные критерии для определения границ режимов.
Распределение давления по высоте аппаратов с газодисперсными средами также, как и амплитудно-частотные важнейшим параметром, так как позволяет определять концентрацию твёрдой фазы и контролировать режим. Первичное деление полного перепада статического давления по высоте на гидростатику, ускорение частиц и трение было предложено . Маскаев и др. выявили, что при скоростях воздуха свыше 8–9 м/с величина трения и ускорения незначительна, и распределение давления отражает главным образом вес столба частиц. Это даёт возможность упрощённо определять плотность слоя, ориентируясь на «гидростатическую» часть. Fuchs и др. , изучая верхнюю часть ЦКС, также пренебрегают ускорением, используя фактически постоянный профиль давления для оценки концентраций и уноса материала. Такой подход прост в реализации и даёт надёжные результаты при корректной геометрии выхода. Напротив, Schlichthaerle и Werther показали, что в нижней зоне распределение давления может искажаться за счёт локального ускорения частиц, поэтому требуются коррекции к «гидростатическим» расчётам. Gungor учёл эти эффекты в численной модели, учитывающей все компоненты распределения давления, — это повысило точность предсказания концентраций. Wang и др. при высоких температурах (до 550 °C) всё же сохраняют упрощённый подход, полагая, что изменения давления с высотой сравнительно невелики и вклад ускорения несущественен.
В работе представлены результаты экспериментов по псевдоожижению частиц опила в плоской лабораторной установке с трапецеидальной нижней частью с контролем пульсаций давления и измерением распределения статического давления по высоте.
2. Методы и принципы исследования
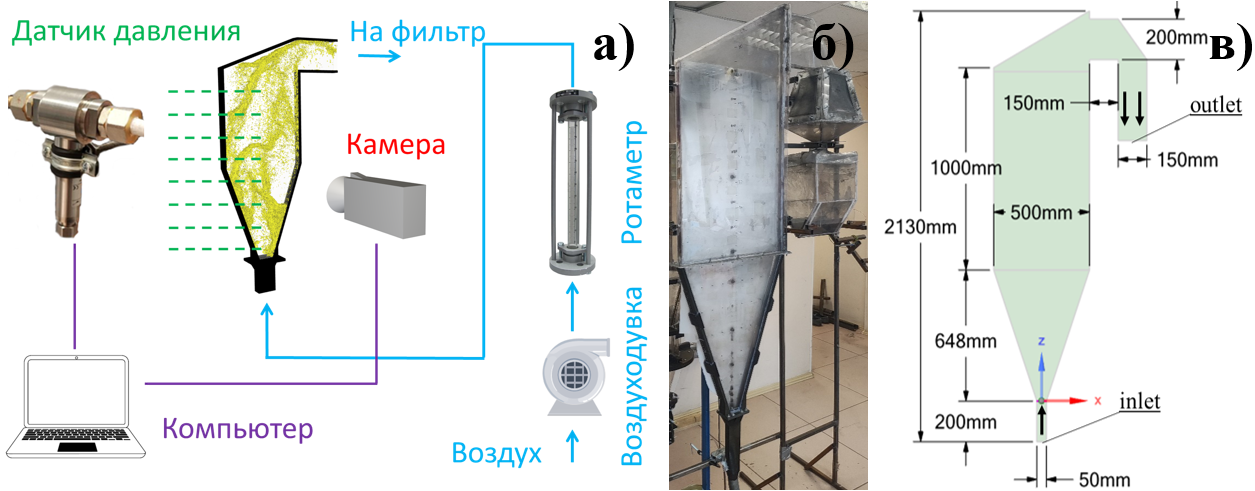
Рисунок 1 - Экспериментальный стенд:
а) схема; б) фотография установки; в) геометрическая модель с нанесенными размерами

Рисунок 2 - Изображения отдельных частиц опила фракции 1-1,25 мм
Среднеквадратическое отклонение, вычислялось по формуле:
где N — последний номер точки в исследуемом ряду данных, q — номер точки в ряду данных (q =1, 2, 3,…, N), yq — точка ряда данных, ym — среднее значение ряда данных:
Спектральный анализ функций пульсаций сигнала давления проводился с помощью дискретного преобразования Фурье, в котором каждая дискретная частота fn вычисляется по формуле:
где N — число точек в исследуемом ряду данных, ∆t — интервал времени между двумя последовательными точками в ряду данных, n — индекс, который обозначает номер дискретной частоты (n = 0, 1, 2,...., N−1), спектральный компонент Yn для каждой частоты вычисляется по формуле:
где q — номер точки в ряду данных (q = 0, 1, 2,…, N−1), yq — точка ряда данных, j — мнимая единица, π — число Пи.
Рассматривалась первая половина спектра, соответствующая положительным частотам (n ≤ N/2). Для получения амплитуды сигнала (Аw) спектральный компонент (4) был нормализован по формуле:
Для оконного преобразования Фурье спектральный компонент Yn для каждой частоты вычисляется по формуле:
где q — номер точки в ряду данных (q = 0, 1, 2,…, N−1), j — мнимая единица, π — число Пи, yqw — оконный сигнал, вычисляемый по формуле:
где yq — точка ряда данных, θq — окно Ханна, вычисляемое по формуле:
В оконном преобразовании Фурье уровень интенсивности каждой отдельной частоты выражается в виде её относительной спектральной плотности, выраженных в Децибелах (10·log10Sy (f)), на локальных участках сигнала по мере его изменения с течением времени, где Sy — спектральная плотность сигнала давления, Па2·с:
где f — частота сигнала.
3. Амплитудно-частотные характеристики пульсаций давления
На рисунке 3 представлены данные по среднеквадратическому отклонению (СКО) пульсаций давления на двух высотных уровнях: 30 мм (рис. 3, а) и 200 мм (рис. 3, б). Для датчика, установленного ближе к решётке (30 мм), видно, что при низких и средних скоростях воздуха (0,4–3,1 м/с), соответствующих режимам устойчивого фонтанирования, СКО возрастает для большинства промежуточных фракций и их смеси. Однако при дальнейшем увеличении скорости (4,6 и 5,4 м/с), когда газодисперсная система переходит в нестабильное состояние и разреженный режим, величина СКО начинает снижаться.
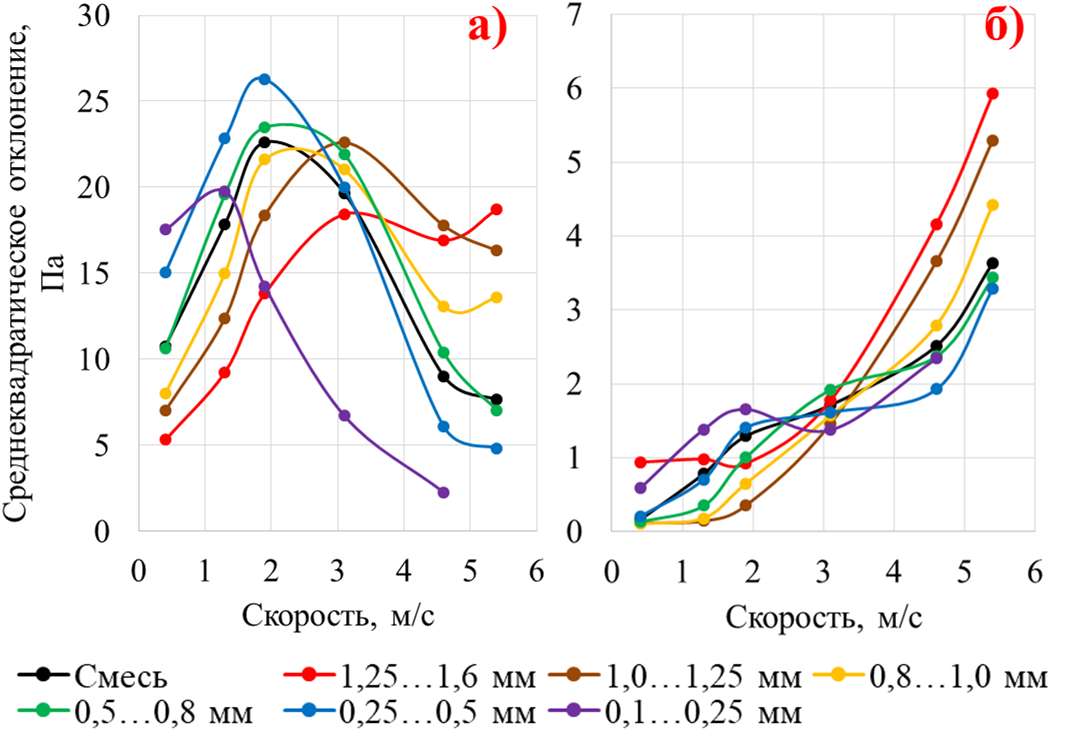
Рисунок 3 - Среднеквадратическое отклонение пульсаций давления при различных составах для точки замера на высоте над входным сечением:
а) 30 мм; б) 200 мм
Для датчика, расположенного у нижней границы слоя (рис. 4, а), пунктирной линией на уровне 4,46 Гц обозначена основная частота гравитационных колебаний пузырькового слоя, высота которого составляет 50 мм; расчёт выполнен по формуле :
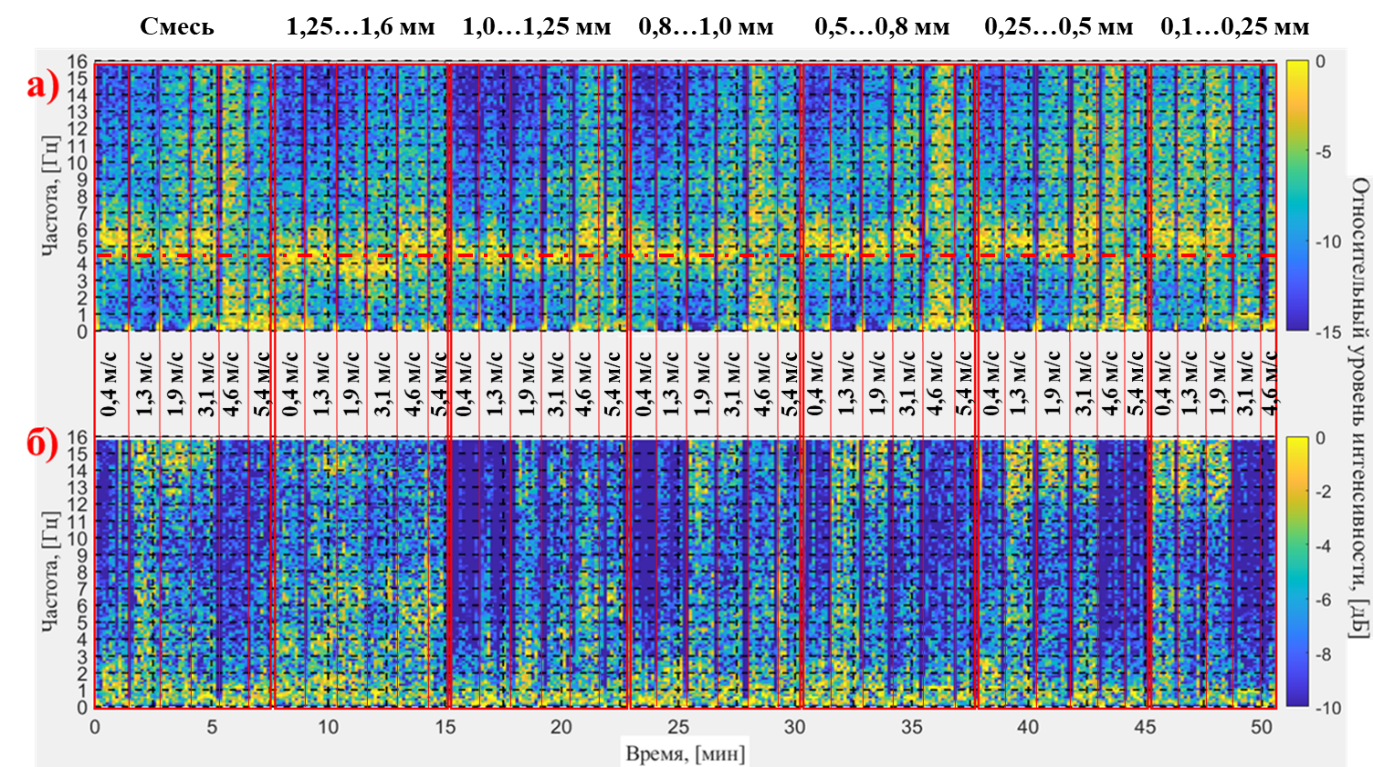
Рисунок 4 - Оконное преобразование Фурье для разверток пульсаций давления при различных дисперсных составах и скоростях на входе в установку для точки замера на высоте над входным сечением:
а) 30 мм; б) 200 мм
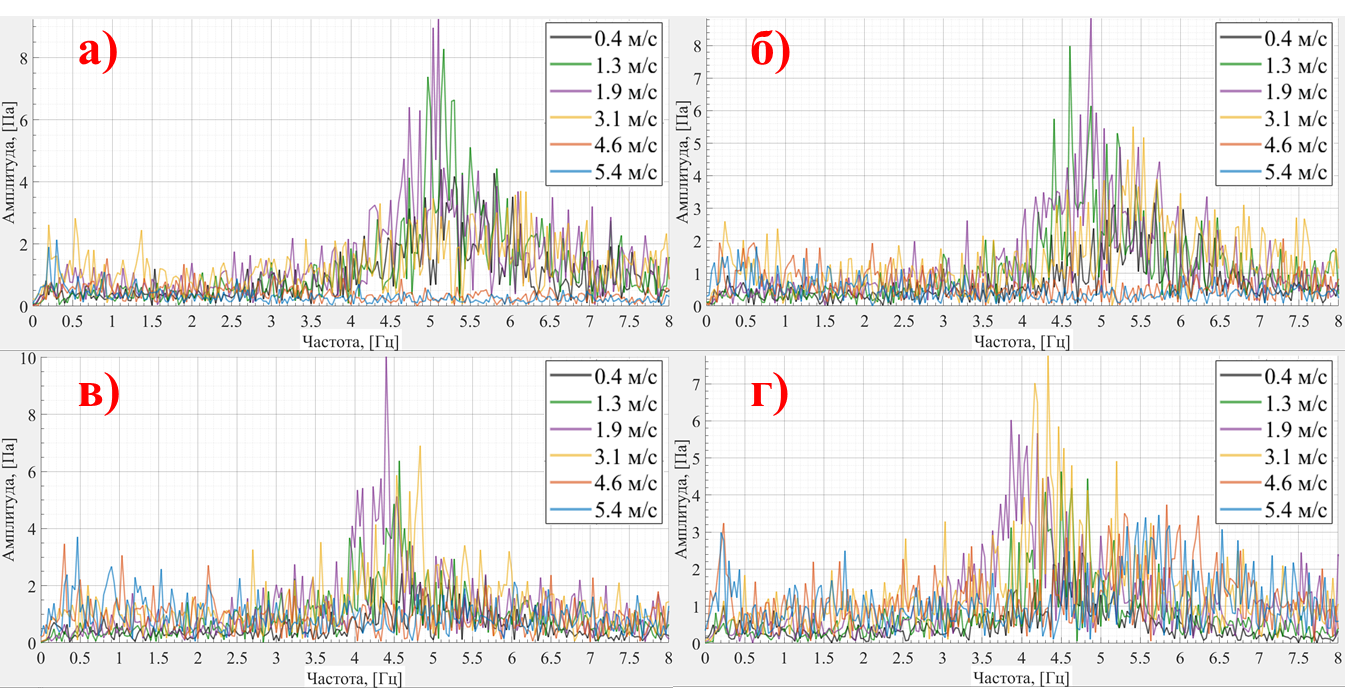
Рисунок 5 - Спектрограммы пульсаций давления в точке на высоте 30 мм над решеткой для различных скоростей воздуха на входное сечение и фракционных составов опила при начальной высоте засыпки 50 мм:
а) фракция 0,25-0,5 мм; б) фракция 0,5-0,8 мм; в) фракция 0,8-1,0 мм; г) фракция 1,0-1,25 мм
4. Распределение давлений и концентраций по высоте
Также были построены распределения статических давлений по высоте для пустой установки («Чистый поток») и для смеси фракций («Загруженный поток») при высоте засыпки 50 мм, на основании которых была произведена оценка объемной концентрации частиц по высоте установки для скоростей воздуха на входе в диффузор wo = 0,4; 1,3; 1,9; 3,1 и 4,6 м/с. При оценке объемной концентрации плотность опила принималась равной 300 кг/м3. Оценка проводилась на основании формулы :
где ρS — плотность частиц, g — ускорение свободного падения, ∆p — разница давлений между двумя высотами, ∆h — расстояние между высотными отметками. Разница давлений между двумя высотами бралась из распределения давления, измеренного напрямую при наличии частиц опила («Загруженный поток») и из распределения разницы давлений загруженного и чистого потока («Вычитание чистого потока»).
На рисунках 6, 7 и 8 для скоростей на входе wo = 0,4; 1,3; 1,9 м/с, соответственно, приводятся распределение избыточного давления по высоте относительно точки 1,4 м для загруженного опилом и чистого потока воздуха наряду с разницей между ними, а также распределение объемных концентраций по высоте. Из рисунков 6–8 видно, что для подобных высококонцентрированных состояний стабильно фонтанирующего слоя опила поправка распределения давления на свободный поток слабо влияет на объемные концентрации. На высотном уровне 30–50 мм свойственны объемные концентрации опила в диапазоне 27–33%, которые слабо коррелируют со скоростью воздуха на входе. При этом на высотном уровне 50–100 мм с ростом скорости объемная концентрация стабильно снижается, составляя 10,5%, 7,4% и 4,2% для скоростей на входе wo = 0,4; 1,3; 1,9 м/с, соответственно. На высотном уровне 100-150 мм, наоборот с ростом скорости объемная концентрация стабильно повышается, составляя 0,29%, 0,76% и 1,69% для скоростей на входе wo = 0,4; 1,3; 1,9 м/с, соответственно.
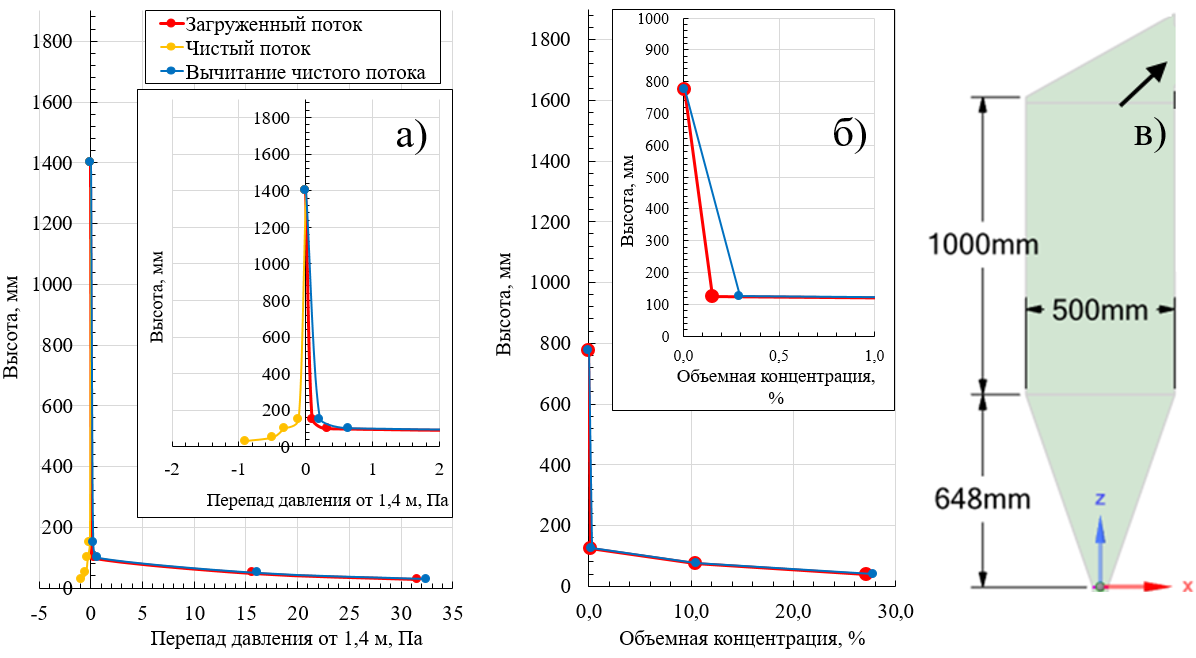
Рисунок 6 - Распределение избыточного давления относительно точки 1,4 м по высоте (а), оценка объёмных концентраций (б) и профиль установки (в) для скорости wo = 0,4 м/с
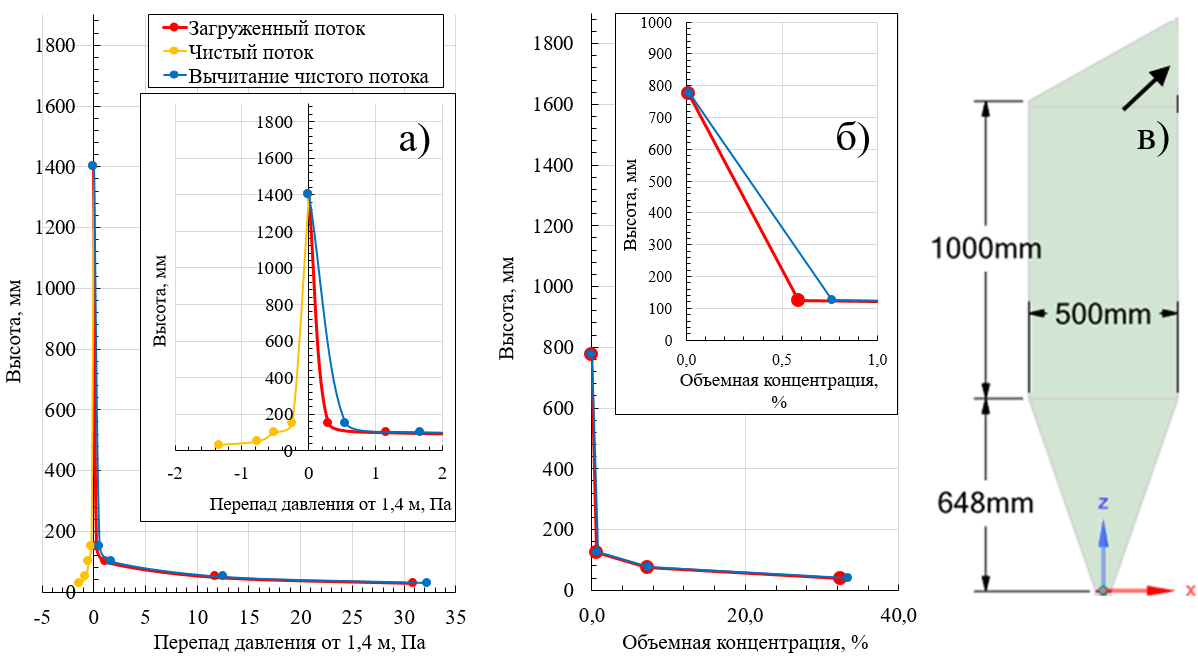
Рисунок 7 - Распределение избыточного давления относительно точки 1,4 м по высоте (а), оценка объёмных концентраций (б) и профиль установки (в) для скорости wo = 1,3 м/с
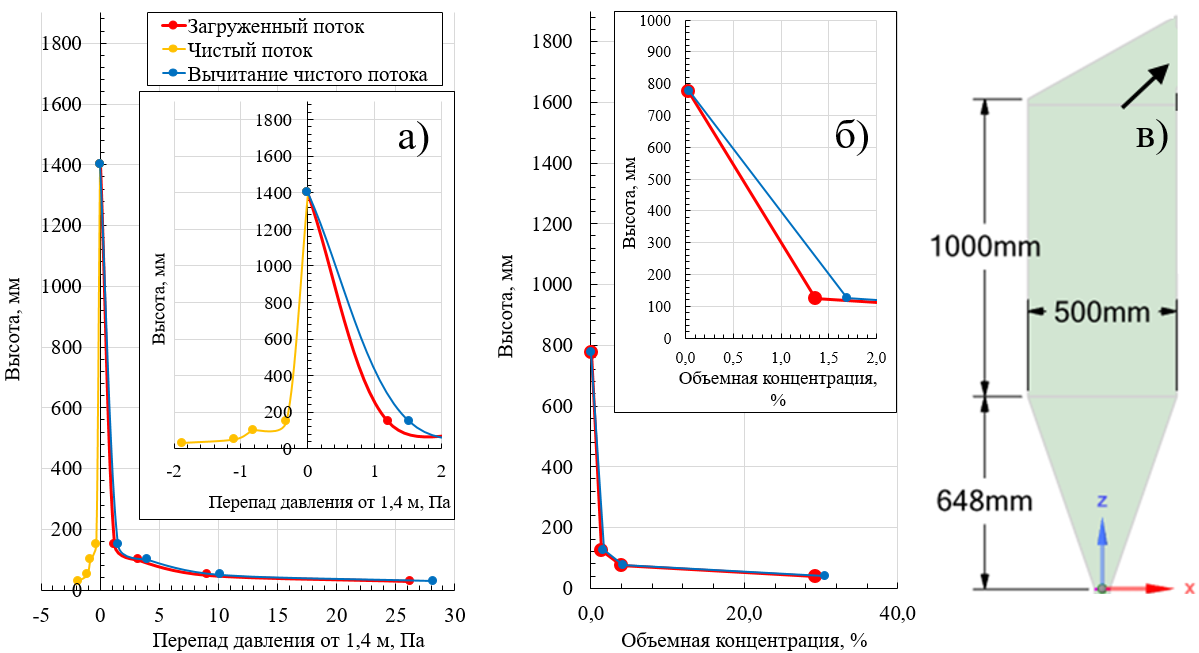
Рисунок 8 - Распределение избыточного давления относительно точки 1,4 м по высоте (а), оценка объёмных концентраций (б) и профиль установки (в) для скорости wo = 1,9 м/с

Рисунок 9 - Фотографии фонтанирующего слоя опила для скоростей wo = 0,4 (а); 1,3 (б); 1,9 (в) м/с
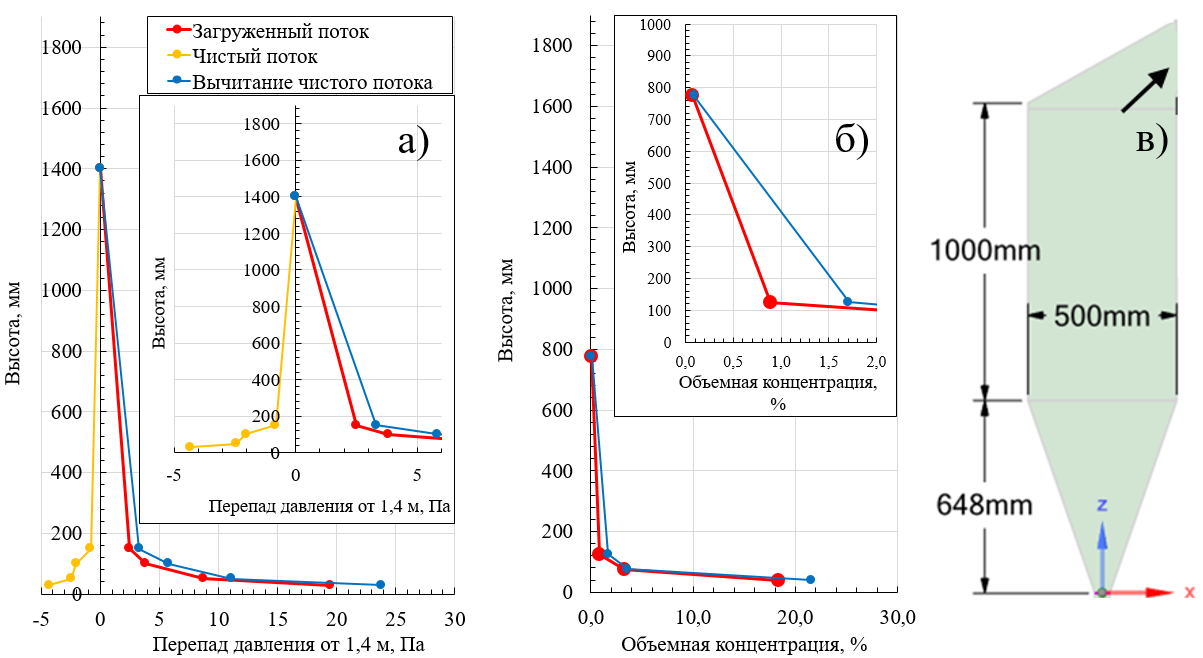
Рисунок 10 - Распределение избыточного давления относительно точки 1,4 м по высоте (а), оценка объёмных концентраций (б) и профиль установки (в) для скорости wo = 3,1 м/с
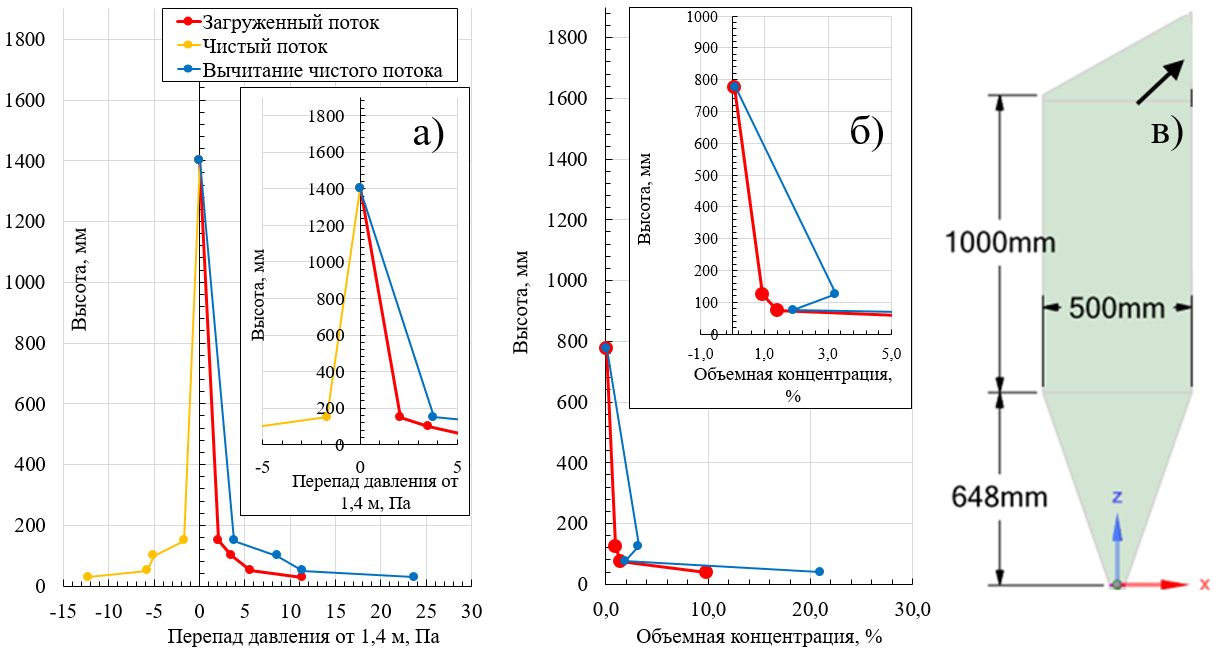
Рисунок 11 - Распределение избыточного давления относительно точки 1,4 м по высоте (а), оценка объёмных концентраций (б) и профиль установки (в) для скорости wo = 4,6 м/с

Рисунок 12 - Фотографии фонтанирующего слоя опила для скоростей wo = 3,1 (а); 4,6 (б) м/с
5. Заключение
Выполнено экспериментальное и численное исследование фонтанирующего слоя частиц опила в плоской холодной модели газогенератора. Для шести фракционных групп (от 0,1…0,25 мм до 1,25…1,6 мм) и смеси фракций проведён анализ пульсаций давления, получены распределения статического давления по высоте, рассчитана объёмная концентрация частиц. Показано существование трёх основных режимов псевдоожижения: стабильное фонтанирование с характерными частотами 3–5 Гц, нестабильное (0,5–8 Гц) и разреженное (до 2 Гц). Установлено, что максимальная концентрация частиц (свыше 30%) наблюдается в нижних слоях, при этом повышение скорости газа приводит к размыванию слоя и увеличению зоны рециркуляции.
Полученные результаты позволяют более точно управлять процессами газификации биомассы и совершенствовать конструктивные решения промышленных установок с учётом формы и размеров частиц опила.
