DIFFUSION AND SOLUBILITY OF HELIUM IN GAMMA-ALUMINA
DIFFUSION AND SOLUBILITY OF HELIUM IN GAMMA-ALUMINA
Abstract
The processes of helium diffusion and solubility in γ-Al₂O₃ crystals have been investigated using high-temperature helium defectoscopy. The flows of desorbing helium have been measured in the range of 200–450°C, temperature dependencies of diffusion coefficients have been calculated, and the effective diffusion activation energy of 0.068 eV has been obtained. The found diffusion coefficients of the order of 10⁻¹⁶ cm²/s are too low for an interstitial diffusion mechanism. Helium solubility in γ-Al₂O₃ samples reaches 4×10¹⁸ cm⁻³ at a temperature of 500°C and a saturation pressure of 50 atm. The observed low rate of helium desorption at 200°C, about a day, indicates its strong interaction with the aluminum oxide crystal lattice, and cation vacancies appear to be preferred positions for helium dissolution. At the same time, the discrepancy between the degassing process times and the desorption flow approximation results indicate the need to develop and use more complex theoretical models to describe helium mass transfer processes in γ-Al₂O₃.
1. Введение
Процессы растворения и диффузии гелия в твердых телах представляют интерес как с фундаментальной, так и с практической точек зрения. Как продукт альфа-распада делящихся материалов гелий образуется в ядерных реакторах, а его накопление в топливе и конструкционных материалах может приводить к ухудшению их прочностных свойств и стабильности, особенно при длительных сроках эксплуатации. Те же соображения относятся и к высокотемпературным ядерным реакторам, в которых гелий используется как теплоноситель. Помимо этого гелий востребован во многих областях промышленности как в виде защитной инертной среды, так и непосредственно расходуемого ресурса. Твердые тела с высокими коэффициентами диффузии перспективны для его энергоэффективной добычи, например, для одноступенчатой мембранной технологии разделения газовой смеси при добыче природного газа. Изотоп гелия-3 является наилучшим материалом для регистрации низкоэнергетических нейтронов, и высококонцентрированные твердые растворы гелия могут стать основой для создания детекторов тепловых нейтронов. В связи с вышеперечисленным актуальным является изучение процессов абсорбции и массопереноса гелия, поиск материалов с высокими значениями растворимости гелия, а также с экстремально высокими или низкими значениями коэффициентов диффузии.
Настоящая работа посвящена определению коэффициентов диффузии и растворимости гелия в гамма-фазе оксиде алюминия методом высокотемпературной гелиевой дефектоскопии . Использование газового масс-анализатора для регистрации потоков десорбирующегося гелия позволяет надежно идентифицировать гелий и проводить измерения с высокой точностью.
2. Методы и принципы исследования
Гелий, как самым легкий инертный газ, целесообразно использовать как детектор для точного количественного определения концентраций дефектов в кристаллах и их идентификации. В тоже время изучение процессов диффузии гелия может выявить особенности механизмов диффузии и взаимодействия нейтральных атомов гелия с ионами кристалла. В данной работе метод гелиевой дефектоскопии был реализован на экспериментальной установке, аналогичной описываемой в . Ее рабочая часть состоит из системы вакуумирования, двухкамерной диффузионной системы с раздельными ячейками насыщения и дегазации, системы калибровки масспектрометра и напуска газа в ячейку насыщения образцов. Регистрирующая часть собрана на базе модернизированного масс-спектрометра МИ-1201Б, работающего в квазистатическом режиме откачки по гелию. Калибровку масс-спектрометра проводили на протяжении всего эксперимента методом двойного расширения гелия заданного давления из известного объема, т.е. сравнивали ионный ток от известного количества гелия с током от гелия, десорбированным из образца.
Методика измерений заключалась в следующем: образец помещали в ячейку насыщения и насыщали гелием при определенном давлении и температуре до установления равновесной концентрации гелия в образце. Была проведена предварительная оценка времени насыщения, само время насыщения выбиралось на порядок больше для гарантии достижения равновесия. После полного насыщения образец закаливали до комнатной температуры и перебрасывали образец в ячейку дегазации, которую затем скачивали на высокий вакуум и нагревали до определенной температуры. Далее накапливающийся газ в ячейке с помощью разнообразных схем расширения перебрасывали в камеру масс спектрометра и регистрировали количество гелия, выделявшегося за определенные, последовательные интервалы времени.
Поскольку изучался гамма-оксид алюминия в виде мелкодисперсного порошка, для работы с ним использовались цилиндрические чехлы, изготовленные из фольги сплава 36НХТЮ. Фольга теоретически тоже может сорбировать и отдавать гелий, поэтому для насыщения и дегазации использовались разные чехлы. После насыщения исследуемый порошок пересыпался в другой чехол, масса образца измерялась каждый раз перед дегазацией на весах Sartorius ME36S I класса точности и погрешностью измерения 0.001 мг.
В данной работе температура насыщения была одинакова для каждого эксперимента и равнялась 500ºС, давление насыщения составляло 25–50 атм. Время каждого насыщения было не менее 30 ч. Типичный вес образцов составлял порядка 50 мг.
Квантово-механические расчеты дают основание ожидать большую энергию связи иона Al3+ и нейтрального атома гелия. Поэтому кристаллы оксида алюминия представляются хорошим объектом для исследования из-за высокой степени ионности, большой ширины запрещенной зоны. У Al2O3 существует целый ряд метастабильных кристаллических модификаций (γ, η, δ, θ и χ фазы), и основная наиболее термодинамически устойчивая фаза α-Al2O3 (корунд) . Все модификации различаются по своему кристаллическому строению (отношению тетраэдрических AlO4 и октаэдрических AlO6 координаций) и ширине запрещенной зоны. При этом термодинамически стабильна α-фаза — единственная фаза, построенная только из октаэдров AlO6, к которой анионы кислорода образуют гексагональную плотную упаковку, а катионы занимают 2/3 октаэдрических пустот. Наши ранние измерения показывают, что гелий практически не растворяется в кристаллах сапфира, значит октаэдрические пустоты не являются энергетически выгодной позицией для размещения атома гелия.
В свою очередь кристаллическую структуру γ-Al2O3 можно описывать как структуру дефектной шпинели (ГЦК-решетка) с катионными вакансиями: □2(2/3)Al21(1/3)O32, где □ — вакансия . Подразумевается, что обычная шпинель (MgAl2O4) содержит 32 аниона и 24 катиона в своей элементарной ячейке — анионы образуют плотнейшую кубическую трехслойную упаковку, 8 катионов находятся в тетраэдрических пустотах и 16 катионов в октаэдрических пустотах. В случае γ-Al2O3 вакансии в количестве 8/3 на одну элементарную ячейку необходимы для сохранения стехиометрии Al2O3. При этом нет однозначного представления о том, где находятся вакансии: в октаэдрических или тетраэдрических пустотах. Кристаллическая структура γ-Al2O3 построена приблизительно на 70% из октаэдров AlO6 и на 30% из тетраэдров AlO4 . Ситуация осложняется тем, что разница между низкотемпературными модификациям γ-, η- и χ- оксида алюминия исчезающе мала, надежного метода идентификации не существует. Так, например, комитет по спектроскопическим стандартам США так определяет разницу в рентгенограммах γ-, η-Al2O3: уширенный пик в одном случае, размытый пик с тем же максимумом в другом .
Исходя из вышеизложенного, можно ожидать, что в гамма-оксиде алюминия катионные вакансии окажутся подходящими позициями для растворения гелия, а их высокая концентрация позволит получить высокую растворимость гелия, что удобно для детектирования десорбирующихся потоков. В качестве исследуемого образца был выбран порошок гамма Al2O3 производства компании "Sasol" Pural марки TM 100 . Порошок был изготовлен из нанокристаллов бёмита (boehmite), гранулированные в порошинки и подвергнутые активации в виде отжига при температуре 550ºС в течение трех часов. Производитель заявляет, что размер нанокристаллов составляет 15 нм, размер порошинки d50=35 мкм, удельная площадь порошка S=150 м2/г (метод адсорбции азота), удельный объем пор 0.9 мл/г, плотность 3.68 г/см3. Основные примеси: C<0.25%, Na2O<0.002%, SiO2<0.015%, Fe2O3<0.015%, TiO2<0.2%.
C помощью анализатора размеров частиц Analysette 22 NanoTec Plus нами было получено распределение порошинок изучаемых образцов по размерам: средний размер оказался равным d50=37 мкм, что подтверждает указанные производителем размеры. Результаты рентгенофазового анализа порошка после многократных циклов «насыщения-дегазации» показывают, что наилучшая оценка по методу Ритвельда получается для двух фаз, при этом область когерентного рассеяния для одной фазы составляет 100 нм, а для другой — порядка 30 нм.
3. Результаты и их обсуждение
Потоки дегазации были измерены для температур от 200ºС до 450ºС. После вакуумирования и нагрева до требуемого значения температура поддерживалась постоянной в течение всего эксперимента с точностью 0.5ºС. Калибровку по гелию проводили обязательно до и после эксперимента, а также через 3–4 точки в процессе измерения потока.
Характерные экспериментальные зависимости потока десорбирующегося гелия из образцов гамма-оксида алюминия от времени установления необходимой температуры представлены на рисунке 1.
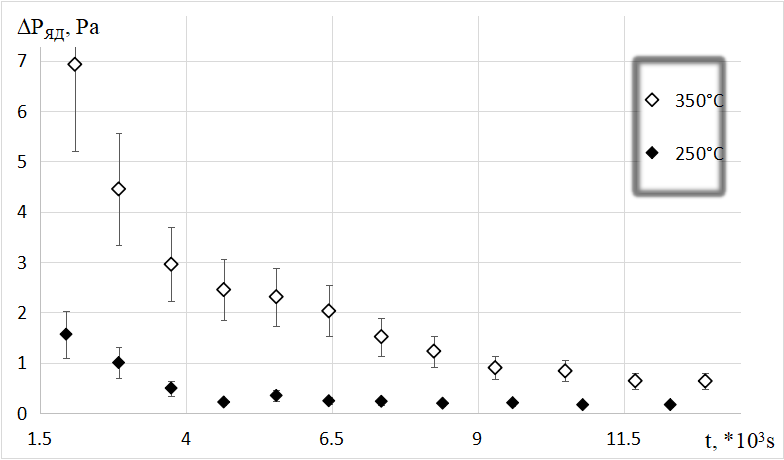
Рисунок 1 - Пример регистрации изменений парциальных давлений гелия от времени при дегазации гелия из образца
Просуммировав количество выделявшегося из образца гелия, можно получить значение растворимости. Для полной дегазации гелия, после десорбционных измерений проводили отжиг образца в течение часа при Т=500ºС. Повторный отжиг в течении еще одного часа показывал отсутствие выделившегося гелия, сигнал по гелию был ниже предела чувствительности масс-спектрометра. Поскольку насыщение проводилось при одной и той же температуре, то и значения полной удельной растворимости (приведенной к одной атмосфере) должны совпадать, что и наблюдается фактически. Различия в значениях обусловлены выходом гелия в самом начале эксперимента при вакуумировании и первоначальном нагреве до температуры дегазации. Была получена растворимость гелия, равная С=(7.8±0.4)·1016 см-3/атм, что для давления насыщения 50 атм дает величину порядка 4·1018 см-3. Подобная величина растворимости является одной из самых высоких в известных нам материалах.
Для обработки потоков и получения коэффициентов диффузии гелия необходимо воспользоваться каким-либо теоретическим решением диффузионной задачи. Наиболее простая модель предполагает единственный тип позиций для растворения и доминирующий механизм диффузии. Например, решение второго закона Фика для десорбции газа в вакуум из предварительного насыщенного образца в форме шара приводит к зависимости потока атомов гелия (dN/dt) от времени (t) вид:
где R0 — радиус шара, D — эффективный коэффициент диффузии, N0 — начальное кол-во частиц, t — время с начала дегазации. Для образца в виде параллелепипеда можно получить похожее решение, но с тройной суммой. В случае больших времен можно пренебречь всеми членами ряда, кроме первого, и получить простую экспоненциальную зависимость, которая будет линейна в полулогарифмических координатах. Выражения для нахождения коэффициента диффузии D для приближения больших времен записываются как:
где A и B — коэффициенты в линейном разложении логарифма экспериментальных потоков дегазирующегося гелия:
Примеры полученных зависимостей вида
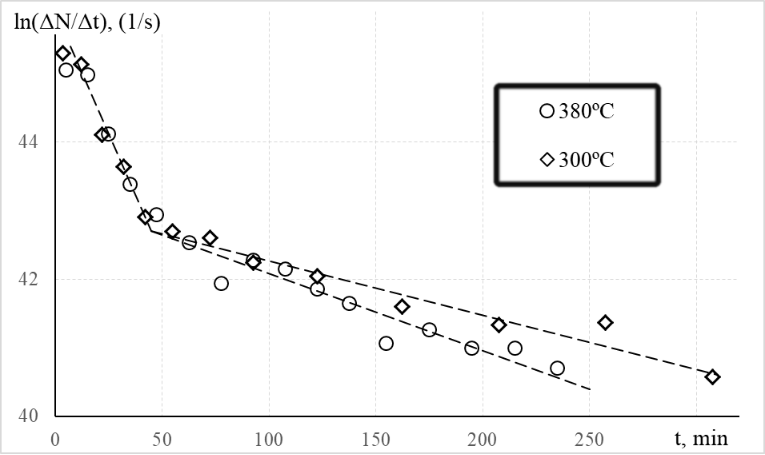
Рисунок 2 - Зависимости логарифмов потока десорбирующегося гелия от времени
Примечание: прямые линии приведены для наглядности
Ключевым параметром в (2) является радиус шара (или линейные размеры параллелепипеда в аналогичном решении), из которого происходит десорбция гелия. Именно этот параметр определяет «масштаб» коэффициентов диффузии. Рассмотрим подробнее структуру образца. С одной стороны имеем средний диаметр порошинки порядка 35 мкм. C другой стороны производитель заявляет об удельной площади порядка S=150 м2/г. Если считать порошинку поликристаллом, состоящим из нанокристаллов и границ зерен между ними (молекулярный азот, использованный для определения площади поверхности, не может диффундировать по границам зерен), то получим удельную площадь, составляющую лишь одну сотую процента от заявленной производителем величины.
Однако если представить порошинку как агломерат нанокристаллов — хаотическое нагромождение сцепленных между собой кристалликов — то между ними будут оставаться промежутки, сопоставимые по размеру этим нанокристаллам, и они будут образовывать систему открытых пор. Что собственно и является причиной использования исследуемого порошка в качестве сорбента. Если принять размер ребра кубического нанокристалла равным 15 нм, то удельная площадь поверхности становится близка к заявленной производителем.
Необходимо отметить, что десорбция гелия с поверхности кристалла, в том числе с поверхности открытых пор, происходит очень быстро, в силу малой энергии адсорбции нейтрального атома гелия. Например, в наших ранних исследованиях диффузия из границ зерен в поликристаллическом диоксиде церия с примесью гадолиния при 400ºС, даже не с поверхности образца, происходила настолько быстро, что почти не регистрировалась в эксперименте, поэтому границу зерна можно было считать эффективным каналом для транспортировки атома гелия из объема зерна в вакуум. Результаты рентгенофазового анализа дают две величины области когерентного рассеяния, которые обычно связывают с размером зерна/кристаллита: 100 нм и 30 нм. Изгиб на графиках на рисунке 2 может быть связан с диффузией из двух разных типов нанокристаллов, возможно, имеющих чуть разную кристаллическую решетку.
Таким образом, мы полагаем, что образец можно рассматривать как совокупность нанокристаллов, причем для простоты примем, что они одинаковые и имеют форму куба с ребром 50 нм (или сфера эквивалентного объема диаметром 62 нм). Обработав потоки гелия, десорбирующегося из образца с этим характерным размером, можно рассчитать эффективные коэффициенты диффузии гелия, которые приведены на рисунке 3 в координатах Аррениуса:
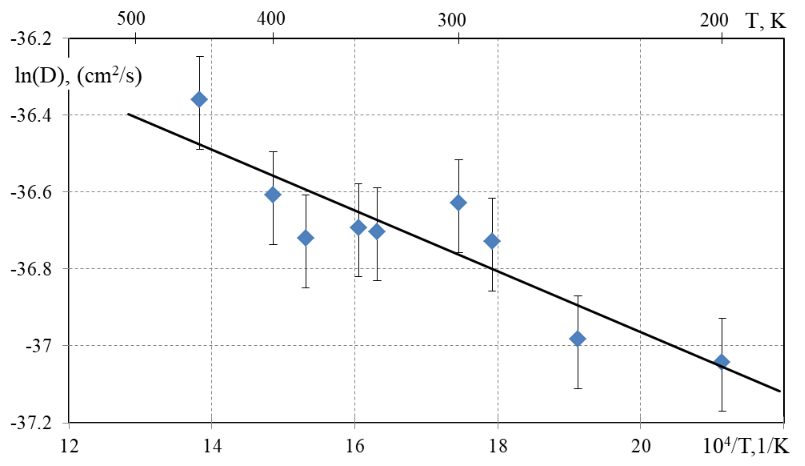
Рисунок 3 - Зависимость логарифма эффективного коэффициента диффузии гелия от обратной температуры
Из данных на рисунке 3 можно сделать ряд выводов. Во-первых, абсолютные значения коэффициентов диффузии очень малы, порядка 10-16 см2/с. Типичные значения D0 для междоузельного механизма диффузии в ионных кристаллах составляют порядка (10-6–10-8) см2/с, а энергия активации диффузии — единицы эВ . Во-вторых, данные аппроксимируются одной прямой, что указывает на существование одного доминирующего механизма диффузии, по крайней мере, при исследованных температурах. Вместе с тем энергия активации диффузии весьма мала: заметно меньше, чем типичные значения для междоузельной диффузии, имеющий порядок единиц эВ.
Нанокристаллы подобного размера можно считать монокристаллами, без дислокаций и границ зерен — считается, что подобным дефектам образовываться энергетически невыгодно. Катионные вакансии могут являться позициями для растворения — «ловушками»; миграция атома гелия будет происходить в две стадии: выход из ловушки, и диффузия по междоузлиям либо до попадания в следующую ловушку, либо до выхода из нанокристалла. Низкие коэффициенты диффузии вкупе с большой величиной растворимости указывают на сильную связь гелия с матрицей γ-Al2O3. Так, при насыщении на 30 атм. и 500ºС среднее равновесное расстояние между соседними атомами гелия составляет порядка 7.5 нм, что вполне сопоставимо с принятым размером нанокристалла 50 нм. Атому гелия требуется сделать всего несколько прыжков до выхода из нанокристалла, но происходит это за макроскопическое время, в течение часов в наших экспериментах.
Однако, низкая энергия активации диффузии на первый взгляд противоречит гипотезе о сильной связи атомов гелия с кристаллом, предположительно при нахождении в катионных вакансиях гамма оксида алюминия. Если гелий сильно связан, ему необходимо преодолеть большой потенциальный барьер при единичном акте миграции. Возможной причиной может являться неприменимость простых решений типа (1) для обработки потоков. В самом деле, для дегазации при 200ºС оценка времени полного выхода 3 тау, согласно решению (1), составляет 6.9 часов. Фактически за первые 4.5 часа при измерении потока выделилось 11.4% гелия, за последующие 19 часов еще 4.9%, а при последующем отжиге при 550ºС — оставшиеся 83.7%. Существуют другие модели для описания десорбции газа, например, дефектно-ловушечный механизм , с помощью которого теоретически можно оценить высоту потенциального барьера при прыжке из ловушки. Качественное описание механизма: если в ловушке есть атом гелия — то эта позиция уже не является ловушкой, и другие атомы свободно мигрируют в этой области кристалла. При понижении концентрации растворенного гелия всё больше ловушек становится свободными, и оставшиеся атомы гелия с больше вероятностью захватываются ловушками, а значит, медленнее выходят из образца. В таком случае при низких концентрациях гелия энергия активации диффузии будет определяться суммой истинной высоты диффузионного барьера и (отрицательной) энергией связи гелия в ловушке. Применение, обоснование применимости и верификация подобных моделей выходит за рамки данной работы.
4. Заключение
В настоящей работе был исследован процесс десорбции гелия из предварительно насыщенных образцов оксида алюминия в гамма-фазе. Были измерены потоки дегазации гелия в диапазоне температур 200–450ºС. Построена температурная зависимость коэффициентов диффузии, получено значение эффективной энергии активации диффузии 0.068 эВ, при этом величина коэффициентов диффузии составляет порядка 10-16 см2/с. Величина растворимости гелия в образце γ-Al2O3 равна 4·1018 см-3 при температуре 500ºС и давлении насыщения 50 атмосфер.
Вместе с тем, в эксперименте наблюдается медленный выход гелия из образца: при 200ºС за сутки десорбировалось всего 16% растворенного газа. Вкупе с низкими коэффициентами диффузии и высоким значением растворимости это может указывать на сильную связь атомов гелия с ионами кристалла. Предпочтительными позициями для растворения гелия при этом являются катионные вакансии в окта- или тетраэдрических пустотах кристаллической решетки гамма-фазы оксида алюминия. Однако малое значение эффективной энергии активации диффузии гелия указывает на неполноту использованного решения диффузионной задачи, и необходимость применения других теоретических моделей для описания процесса десорбции гелия.
