Numerical investigation of parallel-plate magnetic compression line

Picosecond high-power electrical pulses are in demand in experimental physics for studying delayed breakdown processes in various media

Figure 1 - Sectional view of a coaxial magnetic compression line

Note: transformer oil filling the line is not shown

DOI:10.60797/IRJ.2025.160s.23.1

Figure 2 - Typical experimental waveforms of pulse compression in MCL obtained during experiments described in [11]

Note: the pulses are plotted without synchronization

DOI:10.60797/IRJ.2025.160s.23.2

The physical processes underlying the operation of magnetic compression lines are currently under study. First attempts at describing the pulse compression process were based on existing theory for gyromagnetic nonlinear transmission lines, which are high-power microwave devices of similar design

[16]

,

[17]

. This theory was based on the induction of oscillating voltage in the line cross-section by the quasi-periodic precessional motion of magnetization vector in ferrite. However, this theory fails in predicting pulse duration shaped by MCLs, frequently underestimating it by an order of magnitude

[14]

. With the development of full-wave MCL simulation based on numerical solution of Maxwell’s equations, it was found that an important factor affecting MCL operation is its radial inhomogeneity — the presence of two radial dielectric layers, transformer oil and saturated ferrite

[14]

,

[18]

,

[19]

. It was found that such a design, traditionally used solely to increase the dielectric strength of the line (the oil has much higher breakdown voltage than ferrite), has a great effect on the parameters of output pulse of the MCL compared to a hypothetical line fully-filled with ferrite. In this design, the duration of the output pulse becomes directly related to the roundtrip time of the electromagnetic wave between the line conductors due to the dispersion of the formed quasi-TEM (TM00) propagating mode. The dispersion of this mode is of dielectric-waveguide type and manifests itself as the increased group delay of high-frequency signal components compared to low-frequency ones due to former concentrating inside the saturated ferrite layer, consecutively undergoing reflection from the inner conductor and total internal reflection from the boundary between the ferrite and the oil.

Based on the data from microwave engineering literature

The model, as the author’s previously developed model for a coaxial MCL

Here, A is the magnetic vector potential, and M is the magnetization vector. The constants ε0 and µ0 are permittivity and permeability of vacuum, and γ is the absolute value of spin gyromagnetic ratio of an electron, equal to 1.76·1011 rad/(s·T). Material properties are defined through electrical conductivity σ, relative dielectric constant ε, and the properties which are specific to ferrite medium: precession damping coefficient α and magnitude of saturation magnetization Ms. In equation (2) the first term on the righthand side is modified from the usual LLG form to include the coupling to the equation (1).

The system (1)-(2) needs to be expanded into the coordinate form for numerical solution, which is different for Cartesian and curvilinear coordinates due to the presence of the curl operator. Previously, for coaxial MCLs this was done in cylindrical coordinates. In this work the system was expanded for 2D planar geometry, taking the x, y, and z components of the vectors and setting the spatial derivatives in the curl operator with respect to the out-of-plane axis equal to zero.

The geometry of the system is schematically presented in Fig. 3. Fig. 3a shows a 3D sectional view of the parallel-plate ferrite-slab-loaded transmission line, and the magnetizing solenoid. Fig. 3b shows the actual simulation geometry representing the longitudinal cross-section of the structure. It is important to note that in such simulation an infinite extent of the line in the out-of-plane direction is assumed, which can be thought of as a good approximation for the geometry in Fig. 3a when the width of the line is much greater than the distance between the conductors. For a baseline geometry, conductor distance of 16 mm and ferrite filling factor kf of 0.375 was chosen (6 mm thickness of ferrite slab). The parameters of the ferrite were set based on the known values for nickel-zinc ferrite of M200VNP type 

Boundary conditions include the perfect electric conductor boundaries representing the conductors of the line, and scattering boundary conditions at the start and the end of the line, which act as matched terminations and absorb any reflected waves. One of the scattering boundary conditions acts as an excitation, exciting a uniform electric field corresponding to the TEM mode in the parallel-plate line. The waveform and amplitude of the field are set by the parameters of the input voltage pulse. To match the TEM excitation and termination to the inhomogeneous ferrite part of the line, homogeneous oil-filled sections of 40 mm in length are added on both ends of the ferrite-filled section.

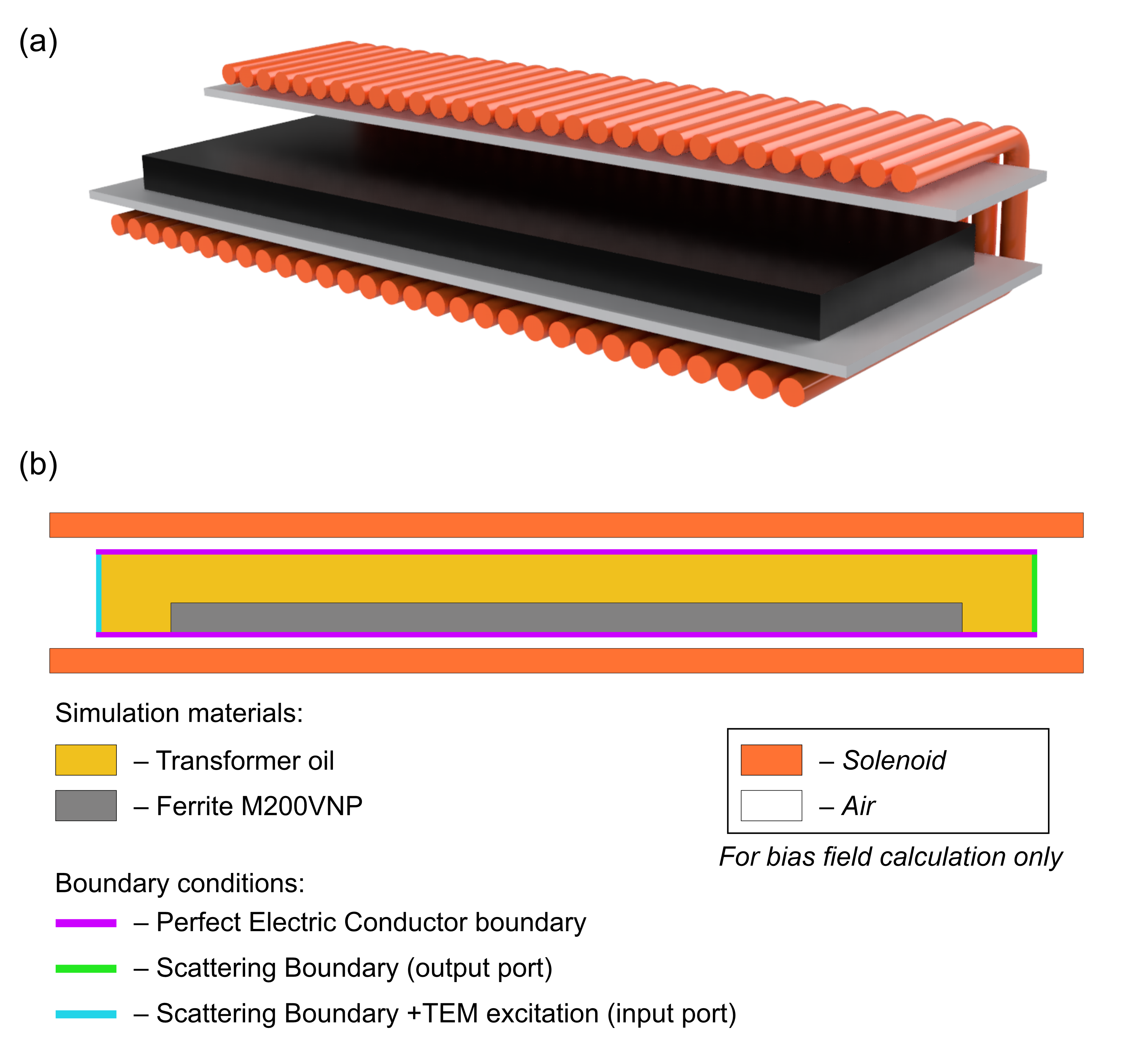
Figure 3 - Sectional view of a parallel-plate magnetic compression line partially filled with ferrite (а); 2D simulation geometry – longitudinal section of the line (b)

DOI:10.60797/IRJ.2025.160s.23.3

The described model was solved numerically using the finite-element method software COMSOL Multiphysics. A preliminary step calculates the static distribution of the magnetizing field from an external solenoid. During the main study step, the system (1)-(2) is solved. The equation (1) is solved in the whole geometry, while equation (2) is solved only in the part of the geometry containing ferrite. The boundary Brown equation

[24]

, which serves as the boundary condition in problems with magnetization in a limited body, is fulfilled here naturally due to the weak-form implementation of the finite-element method.  For the discretization, a triangular mesh with quadratic vector elements was chosen. Time stepping is performed using the generalized-alpha algorithm, and the time step and mesh size are chosen using the method described in

[23]

.

The first set of numerical experiments consisted of varying the duration of the input pulse in the baseline geometry and observing its influence on the output waveform of the line. In nonlinear dispersive wave systems, the shape, duration, and amplitude of the input wave affect the waveform transformation

The shape of the input pulse in calculations was set as a Gaussian function. Following the experimental convention, the pulses of negative polarity were used. The value of bias magnetic field was set to 100 kA/m. It was found that for different input pulse amplitudes the general modes of pulse shaping remain the same. Typical waveforms of these modes are presented in Fig. 4 for input pulse amplitude of 1400 kV. Depending on the input pulse duration, the output pulse consists of one or several nonlinear oscillation peaks, which can be recognized as solitary waves or solitons

If on the contrary, pulse duration is quite long, for example 1400 ps for the studied conditions, the line operates in the nonlinear microwave regime, generating several peaks of soliton-like oscillations (Fig. 4b). In this regime peak power increase can achieve 2.6 times, however, the formation of additional unwanted peaks of relatively high amplitude prohibits the use of this regime for pulse compression.

It is evident that in the context of pulse compression the operating mode of the line is set by the duration of the input pulse at a given amplitude. One must choose the input pulse duration as an optimum between the amount of unwanted post-pulse signal and the desired peak power increase, since these quantities are inversely related. Usually, in MCL experiments the power increase of 2 is chosen. Such a mode is presented in Fig 4c, with an input pulse duration of 560 ps. In these conditions peak power is increased twofold at the cost of the formation of the second peak. However, the amplitude of the second peak is relatively low, 1/3 of the amplitude of the main peak. This operation mode is similar to the usual mode implemented in multi-gigawatt coaxial MCLs. Comparison with sech2(t) function presented in Fig. 4c shows good agreement of the main peak with the expected soliton waveform.

Overall, the conducted set of numerical experiments leads us to the following conclusions. The parallel-plate ferrite line exhibits the pulse shaping modes analogous to those observed in coaxial ferrite lines. It nonlinearly transforms a high-voltage bell-shaped pulse into a pulse consisting of one or several solitons with a shape close to sech2(t) curve, depending on input pulse duration at a given amplitude. Analogously to other soliton systems, for bell-shaped input pulses the number of generated soliton peaks can approximately be found as the integer part of the relation of input pulse duration t­in to a characteristic time

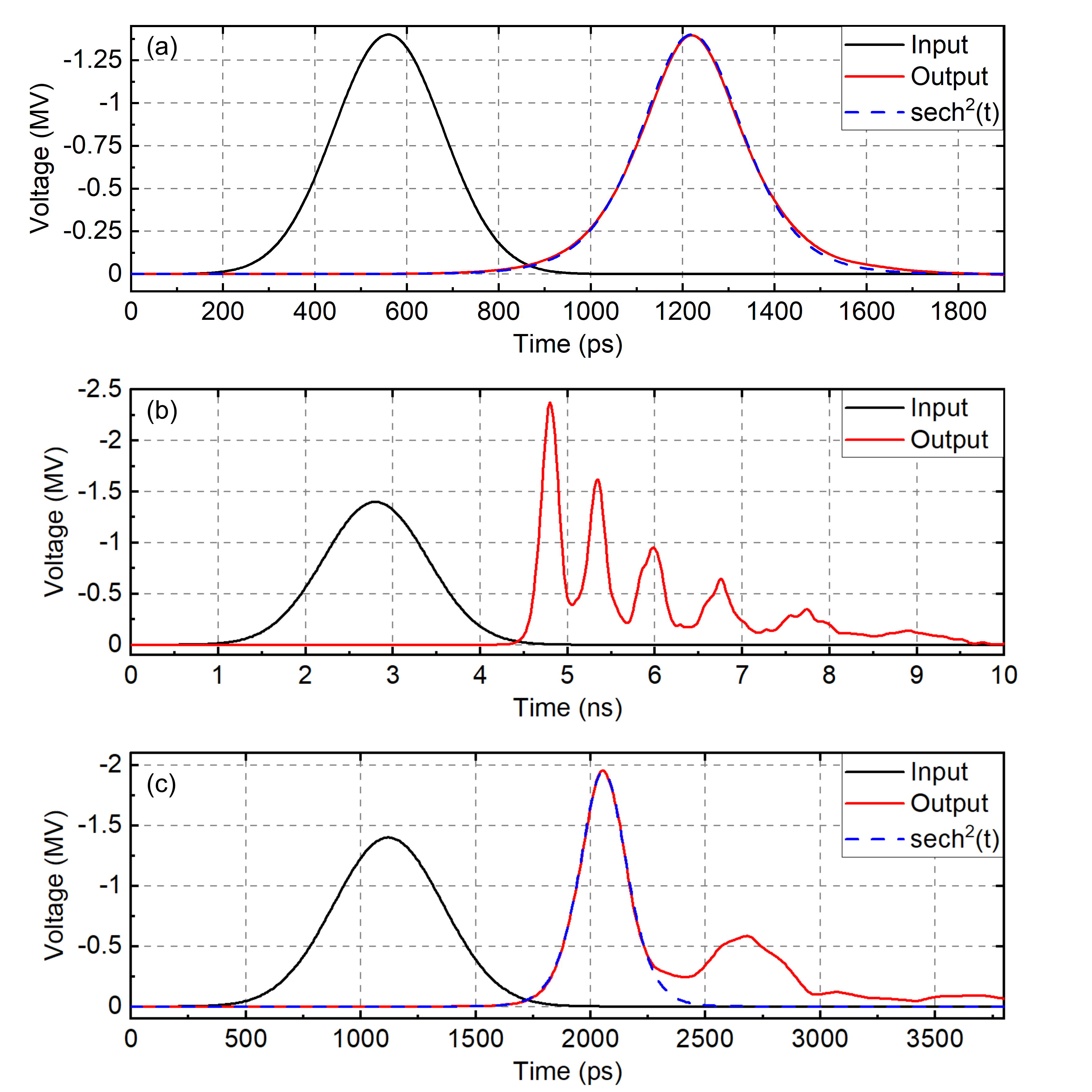
Figure 4 - Typical modes of pulse shaping: 

(a) single-soliton shaping, (b) multi-soliton decomposition (nonlinear oscillations generation), (c) optimal pulse compression

Note: the input and output pulses are plotted without synchronization

DOI:10.60797/IRJ.2025.160s.23.4

From the waveforms presented in Fig. 4a it was found that at the given input pulse amplitude the duration of a single soliton and, hence, the value of

$\tau$

is equal to 260 ps. In the case presented in Fig. 4a, the relation t­in/

$\tau$

≈ 1.1, and no additional solitons are formed; the input Gaussian pulse is only reshaped to match the sech2(t) soliton waveform. In Fig. 4b, t­in/

$\tau$

≈ 5.4, hence 5 soliton peaks are formed, and the leftover energy forms a dispersive sixth peak

[25]

due to an excessive value of t­in. Finally, in Fig. 4c, t­in/

$\tau$

 ≈ 2.2, and correspondingly, two soliton peaks are formed.

Typical dynamics of pulse compression obtained in the simulations for the optimal compression mode is presented in Fig. 5. The transformation of the pulse consists of initial pulse sharpening in a shock-wave manner (0 – 40 mm), subsequent appearance of oscillations on top of the pulse due to dispersive decay of sharpened pulse front (40 – 80 mm), and the decomposition of the pulse into two solitons, during which the first one obtains higher amplitude and velocity than the second one (80 – 360 mm). This dynamics is analogous to the one seen in coaxial MCLs

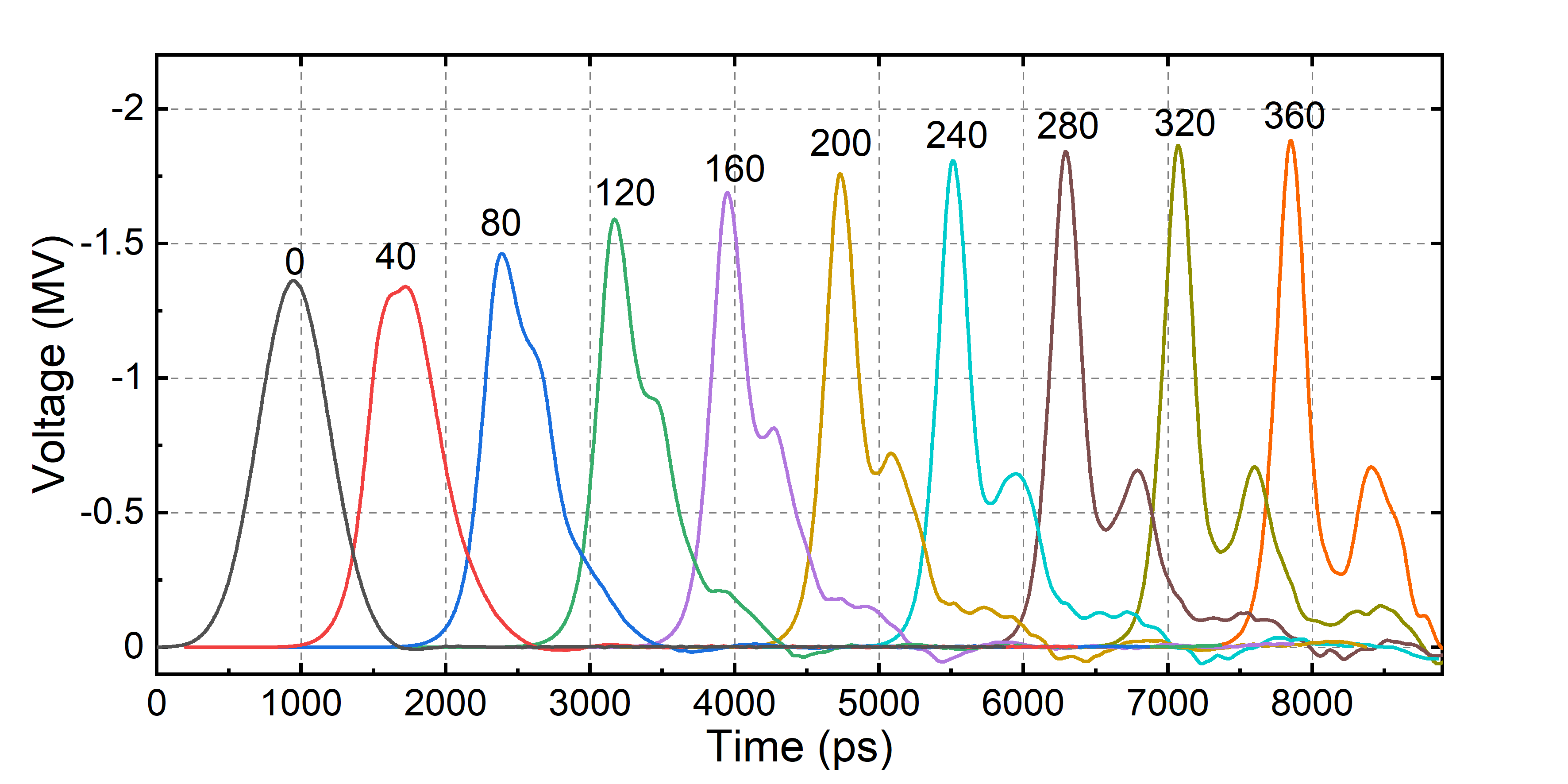
Figure 5 - Dynamics of pulse compression on optimal mode

Note: the number above each pulse corresponds to the distance from the start of the ferrite section in mm; the pulses are plotted without synchronization

DOI:10.60797/IRJ.2025.160s.23.5

It is apparent that to obtain a desired pulse shaping mode in a given line, one needs to know its value of

$\tau$

. In general,

$\tau$

will depend on line cross-sectional geometry due to the waveguide nature of its dispersion, and the value of biasing magnetic field and input pulse amplitude due to nonlinear ferrite properties. Experimental observations on coaxial MCLs show that for similar pulse parameters, conductor distances and ferrite filling factors of the line, the value of

$\tau$

is roughly independent of pulse amplitude and is close to the calculated time of electromagnetic wave propagation between line conductors T0 multiplied by 2

[14]

. For the studied geometry, the value of 2T0 is approximately 270 ps, which is indeed close to 260 ps found from described numerical calculations.

As was stated above, there exists an optimum pulse compression mode, in which peak power of the pulse is increased by a factor of 2. To obtain such a mode, one must supply an input pulse with specific amplitude Vin, opt and duration (FWHM) t­in, opt for a line of a given cross-sectional geometry. The set of numerical experiments described in this subsection is conducted for evaluating the dependencies between Vin, opt, t­in, opt and compression parameters for different values of ferrite filling factor kf, defined as the ratio of ferrite slab thickness to the distance between line conductors.

The results of numerical experiments are presented in Fig. 6. Fig. 6a shows the dependence of t­in, opt on Vin, opt. For low pulse amplitudes (300-400 kV), the optimal pulse duration is practically independent of kf and decreases with increase in input pulse amplitude. With further increase in pulse amplitude, the curves for different values of kf diverge and for pulse amplitudes of more than ~1000 kV the optimal pulse duration is practically independent of pulse amplitude, and decreases with decrease in kf.

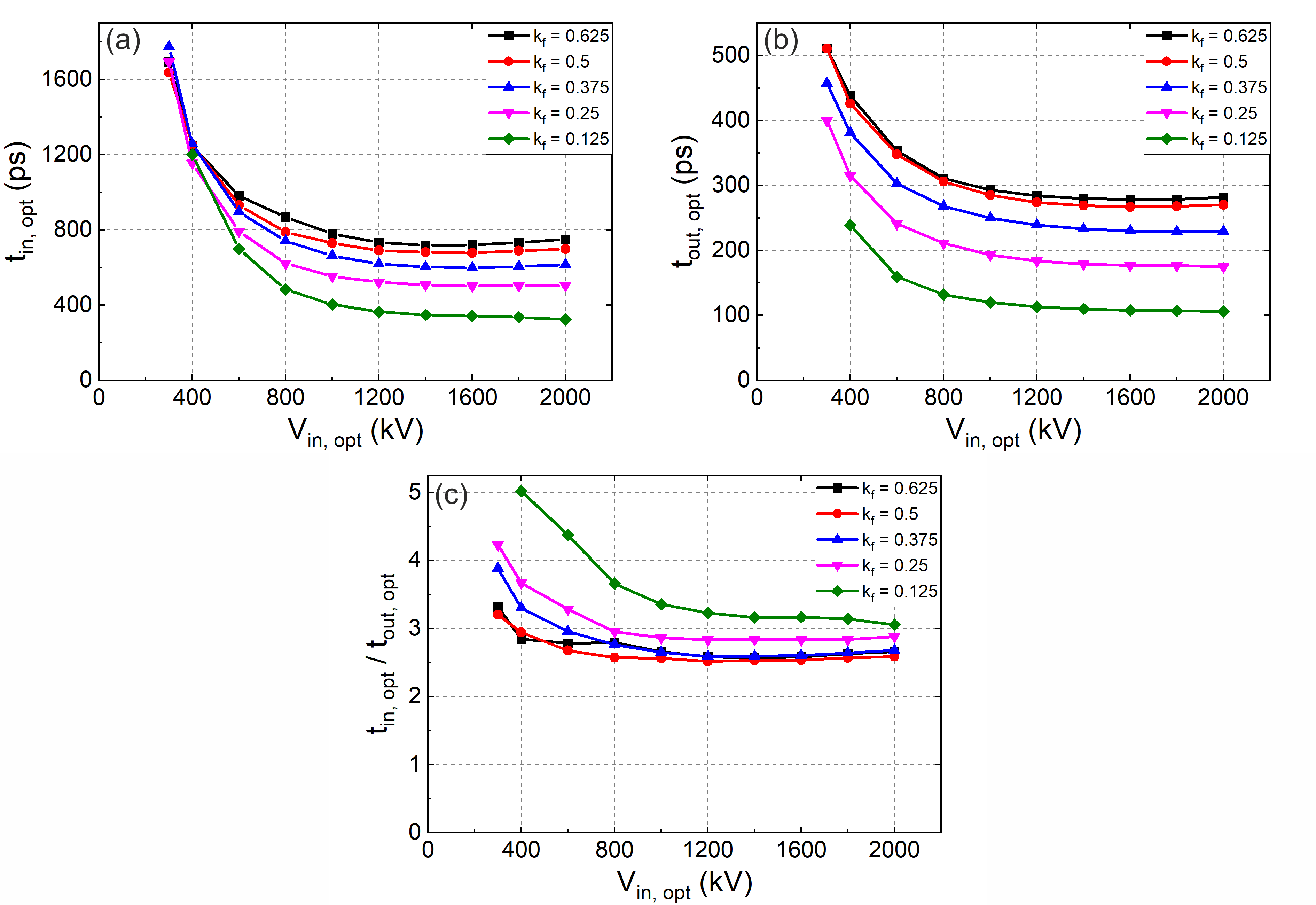
Figure 6 - Variation of optimal compression mode parameters with input pulse amplitude Vin, opt and ferrite filling factor kf :

(a) optimal input pulse duration t­in, opt; (b) output pulse duration t­out, opt; (c) compression coefficient

DOI:10.60797/IRJ.2025.160s.23.6

The observed dependence can be explained in terms of dispersion characteristics of dominant quasi-TEM mode (TM­0 mode in the case of a parallel-plate line) with a gyromagnetic filling

[18]

. The optimum pulse duration can be found from a characteristic time

$\tau$

as t­in, opt ≈ 2

$\tau$

, and

$\tau$

directly depends on the shape of the dispersion curve of the line. In a line with composite ferrite-dielectric filling, the dispersion curve changes with a change in magnetic field of the pulse, as described in

[18]

. At low pulse amplitudes the frequency of gyromagnetic precession, determined by the magnetic field in the line, is lower than the inflection frequency of the quasi-TEM dispersion curve. Accordingly, the value of

$\tau$

is determined by the average value of magnetic field in the cross-section of the line, which in this case depends only on pulse amplitude and not on the ferrite filling factor kf. Thus, t­in, opt also depends only on pulse amplitude.

With the increase in pulse amplitude, the magnetic field and the frequency of gyromagnetic precession increase, and t­in, opt decreases, as can be seen in Fig. 5a for voltages of 300–400 kV. When the frequency of gyromagnetic precession approaches the kf-dependent inflection frequency of quasi-TEM dispersion curve, the latter starts influencing the value of t­in, opt as well (~500 kV). At high pulse amplitudes and corresponding magnetic fields (>1000 kV in Fig. 5a) the frequency of gyromagnetic precession becomes much higher than the inflection frequency of quasi-TEM dispersion curve, and only the latter influences the value of τ and t­in, opt. Due to this, optimal pulse duration becomes independent of pulse amplitude and is determined by the dispersion characteristics of the quasi-TEM mode.

The value of 

Here D is distance between line conductors and c is speed of light in vacuum. As can be seen from (3), T0 has a linear dependence on kf. Due to that, τ and tin, opt are proportional to kf as well, which explains the increase of the plateau level of the curves in Fig. 5a with increasing kf.

Fig. 5b shows obtained dependencies of output pulse duration t­out, opt on Vin, opt for different values of kf. It is seen that output pulse duration exhibits similar behavior to tin, opt, showing the kf-dependent plateau at input voltages with amplitude greater than ~1 MV. The reason for this can be assumed to be the proportionality between output pulse duration and

The compression coefficient curve at kf = 0.125 is noticeably different from the curves at other kf values. Moreover, it was found that at kf values greater than 0.625, the generated signal obtains additional modes of oscillation, which disrupt the compression process, hence such kf values are absent from the above analysis. At the moment, the author cannot present a clear explanation of these effects. In this work these problems were not studied further, and can only be stated as the evidence to the complexity of phenomena occurring in ferrite-filled nonlinear transmission lines.

However, from a practical point of view, the regimes with low and high values of kf are of low importance, because due to design limitations and the need for high dielectric strength only the values of kf close to 0.4-0.5 would be realized in practice. In view of that, for practical purposes, the most important effect described here is the existence of two regimes of optimal compression based on input pulse amplitudes. For pulse amplitudes lower than some threshold value (1 MV in this case) the first regime of optimal compression is realized, in which the durations of input and output pulse are influenced by input pulse amplitude due to gyromagnetic processes. For pulse amplitudes higher than the threshold value, a second regime of optimal compression is realized, in which the durations of input and output pulse are influenced only by the geometrical parameters of line cross-section due to quasi-TEM dispersion processes. Due to the similarity in quasi-TEM type of dispersion, the existence of two regimes should hold true for traditional coaxial MCLs as well. Applying this distinction to the main body of experimental data on MCLs

In this paper, a numerical analysis of parallel-plate magnetic compression line was conducted. The results of numerical experiments show that the modes of pulse shaping in such a line are analogous to those of traditional coaxial magnetic compression lines, and that traditional pulse compression mode with twofold peak power increase can be achieved, as well as single-soliton shaping and high-power microwave generation. It was also shown that at voltages over ~1 MV due to partial filling of the line with ferrite the duration of the output pulse is set by the dispersion properties of the dominant dispersive quasi-TEM wave, which is seen as the independence of output pulse duration on pulse amplitude, and its dependence on ferrite filling factor. It was found that, analogously to coaxial magnetic compression lines, the duration of output pulse in this regime is close to the roundtrip time of electromagnetic wave between line conductors. The found analogy between the processes in magnetic compression lines of parallel-plate and coaxial geometries can be used to facilitate analytical treatment of nonlinear pulse compression in such systems due to reduced complexity of the mathematical problem in parallel-plate geometry compared to coaxial one. Parallel-plate geometry might also be advantageous in practice compared to coaxial one due to the simplified fabrication process, however, for such comparison breakdown processes need to be carefully considered.