A MODEL OF FLUCTUATION VARIABILITY ON THE EXAMPLE OF WHEAT LEAF PLATES
A MODEL OF FLUCTUATION VARIABILITY ON THE EXAMPLE OF WHEAT LEAF PLATES
Abstract
Wheat leaf plates, like all grains, have longitudinal veining, which creates a difficulty in studying the fluctuating asymmetry (FA) of homologous bilaterally symmetrical structures. To determine FA (non-directional deviation from zero of the difference between the right and left structures) and directional asymmetry (DA, a shift to one side), the method of geometric morphometry was used. The advantage of this method is the alignment of the mark coordinates and the removal of the size component in a sample of plate samples.
100 marks were placed along the contour of the leaf, 50 evenly on each side, and the FA and DA values were determined. The presence and significance of directional asymmetry was determined by two-factor analysis of variance using the factor "side", and FA was determined by the interaction between the factors "leaf" and "side". The magnitude of fluctuating asymmetry was determined by the difference in variance of the left and right labels. The directional asymmetry was found by subtracting the mean value from the difference |L - R|, where L and R are the variance of the left and right labels, respectively.
A comparison of leaf plate asymmetry of 4 populations grown at different fertilizer doses was carried out, from an intensive dose of mineral fertilizers to a high-intensive one that included organic (cattle manure) and mineral fertilizers (ammophos). Two varieties of wheat were used as test material: one winter and one spring wheat.
Significant decrease in development stability (increase in FA) with increasing fertilizer dose was obtained in winter wheat plants. Spring wheat showed a gradual decrease in FA from the first to the fourth fertilizer dose. Both types of asymmetry showed positive correlation relationship: winter wheat Spearman's r = 0.61 and 0.64 – spring wheat.
Modelling by regression analysis showed that the response (FA) of the winter variety was in exponential dependence on both factors: dose (χ2 = 264.5) and directional asymmetry (χ2 = 167.5; everywhere p << 0.05). The exponential model explained 81.7% of the variance in the residuals.
For spring wheat, a polynomial dependence model was obtained that explained 73% of the variance in residuals and showed only the directional asymmetry factor to be significant (χ2 = 14.1; p = 0.0002). Tweedie's exponential distribution was used in both models. The criterion for evaluating the significance of the Wald regression coefficients showed results confirming those of the xy-squared (χ2) criterion. Thus, in spring wheat leaves, fluctuational variability decreased with increasing fertilizer dose and showed a polynomial model of directional asymmetry dependence, according to which increasing dose decreased asymmetry, in contrast to winter wheat, which showed a persistent increase in developmental instability and overall asymmetry with increasing fertilizer dose.
1. Введение
Флуктуационная изменчивость – это колебание величины морфологических, биохимических, а также других показателей около среднего значения, генетически обусловленного нормой реакции.
Существует несколько гипотез объясняющих природу флуктуационной изменчивости. В листовых пластинах, в том числе злаковых растений, ее определяют по величине флуктуирующей асимметрии (ФА) левых и правых гомологичных признаков, например по ширине листовой пластины или любых других счетных или мерных билатерально симметричных структур.
Под термином «стабильность развития» понимается биохимический статус организма с определенным уровнем ФА. Известно, что у древесных растений высокое отклонение величины ФА в сравнении с контролем означает снижение стабильности развития популяции , .
Направленная асимметрия – это направленный сдвиг разности между левыми и правыми величинами в одну из сторон, левую или правую, которая часто встречается в растениях из-за фототаксиса – синтеза клеток по направлению к источнику освещения и регулируется фитогормонами в меристеме. В отличие от ФА, направленная асимметрия наследуема и теснее связана с генотипом.
Для злаковых характерны оба вида асимметрии. Так в проведенных ранее исследованиях замечено, что в листьях пшеницы, ржи, ячменя и овса в 80% случаях встречались оба вида асимметрии в равном или неравном соотношении , . На долю того или иного вида асимметрии оказывали влияния климатические условия года, доза вносимого удобрения и способ обработки почвы .
Наиболее точно индекс ФА находят в смешанном 2-х факторном дисперсионном анализе (лист × сторона) с вычетом ошибки измерения, где фактор «лист» является рандомным фактором, а «сторона» – фиксированным.
Метод геометрической морфометрии позволяет с использованием программных средств (TPSDig2, MorphoJ) искусственно увеличить число признаков в виде равномерно расставляемых меток по краю правой и левой половины листа .
Консенусная фигура пластины строится с учётом расположения всех меток, дисперсии ХУ координат меток и обеспечивает определение ФА и НА по совокупности наносимых меток. Соотношение ФА/НА указывает на соотношение фенотипического и генотипического компонентов асимметрии, а доля ФА указывает на изменчивость стабильности развития .
Наиболее удобным для изучения фактором, влияющим на асимметрию билатеральных признаков злаковых, представляется доза удобрения, вносимого под зерновую культуру, т.к. питательные вещества стимулируют рост вегетативных и генеративных органов растения и повышают конечную биологическую продукцию зерна в колосе.
Целью работы было построить модель изменения стабильности развития в виде величины ФА в зависимости от направленной асимметрии и с учетом дозы вносимого удобрения. Для сравнения использовалось два распространенных сорта пшеницы, один сорт озимой и один – яровой.
2. Методы и принципы исследования
2.1. Места сбора
Флаговые листовые пластины пшеницы (Triticum aestivum L.,1753), прилегающие к колосу, собирались во второй половине июля 2019 г. (озимая, сорт Поэма) и в 2020 г. (яровая, сорт Грань) на территории Федерального Аграрного Научного центра (г. Суздаль, Владимирская обл.), где на серых лесных почвах Суздальского Ополья проводится многолетний адаптивно-ландшафтный эксперимент с разработанной системой севооборота и внесения удобрения.
Использовалось 4 дозы минерального удобрения нитроаммофоска (NPK). По принятой технологии были внесены следующие дозы:
1) интенсивная (N90P90K90);
2) высокоинтенсивная (N120P120K120);
3) интенсивная органоминеральная (60 т органического удобрения + N90P90K90);
4) высокоинтенсивная органоминеральная (80 т органического удобрения + N120P120K120).
Все дозы вносились непосредственно перед посевом.
Площадь участка составляла 35 м2 (5×7), а контролем служили полосы шириной 1 м, разделявшие делянки с различными дозами удобрения. Листовые пластины собирались рандомно, избегая края делянки 1 м шириной. Отбирались пластины с длиной 16-18 см, затем выбирались симметричные пластины без изгибов и поражения микроорганизмами.
Таким образом, с каждой делянки (всего четыре) было отобрано 25-30 пластин. Сначала они вымачивались сутки в бытовом 5%-м детергенте, затем высушивались и наклеивались на бумагу нижней стороной наверх и сканировались с помощью сканера Canon MF3010 (dpi 300) вместе с мерной линейкой, градуированной по ГОСТ. Изображения сохранялись в формате JPG.
2.2. Статистическая обработка и моделирование
Основные статистики выборок |L – R| определялись в программе STATISTICA10 (StatSoft Ink, 2011). Нанесение основных меток (true landmarks, программа TPSDig2) проводилось в точку основания пластины, лишенной лигулы (язычка) и на верхушку пластины (апекс). Вспомогательные метки (semilandmarks) наносились с равным интервалом по каждой стороне листа по 50 меток.
С помощью программы MorphoJ (Klingenberg, 2019) проводилось усреднение и выравнивание всех контуров листовых пластин, таким образом, создавалась консенсусная форма и по дисперсии координат меток (суммы квадратов координат Х и У) рассчитывалась дисперсия каждой правой и левой метки (программа TPSRelw). По разности дисперсии рассчитывалась флуктуирующая асимметрия. Значимость ФА тестировалась в 2-х факторном дисперсионном анализе по эффекту взаимодействия факторов «лист» и «сторона». Присутствие направленной асимметрии определялось по значимости эффекта фактора «сторона». Выборка, содержащая ФА не содержала примесь НА, т.к. из разности L – R по абсолютной величине вычиталось среднее значение. Полученное значение и служило величиной направленной асимметрии.
Для проверки на присутствие антисимметрии была проведена визуальная проверка на выбросы, а также находился коэффициент корреляции Спирмена на отрицательную связь между значениями левого и правого признаков в выборках.
Для построения модели ФА – НА – доза удобрения был использован метод регрессионного анализа. Он был удобен в том, что позволял оценить влияние двух факторов (НА и величины дозы удобрения) на результирующий отклик, в нашем случае индекс флуктуирующей асимметрии.
3. Основные результаты
3.1. Описательная статистика
Все выборки |L – R| (L – дисперсия левой метки; R – дисперсия правой метки) обладали непараметрическим распределением (К-С тест р < 0,05) из-за высокой дисперсии у верхушки и основания листа и в большинстве случае содержали примесь направленной асимметрии, но большую долю асимметрии занимала флуктуирующая асимметрия.
Не было получено отрицательной корреляции между L и R, т.е. антисимметрия отсутствовала. Предварительно был проведен факторный дисперсионный анализ по влиянию дозы и направленной асимметрии на ФА двух сортов пшеницы. Значимыми был фактор дозы (df = 3; F = 7,5; p << 0,05), который влиял на ФА в зависимости от сорта (df = 1; F = 5,24; p < 0,05). 4-я доза способствовала повышению индекса ФА озимой пшеницы. Этот сорт показал высокую корреляцию ФА/НА в сгруппированных данных (Рисунок 1).
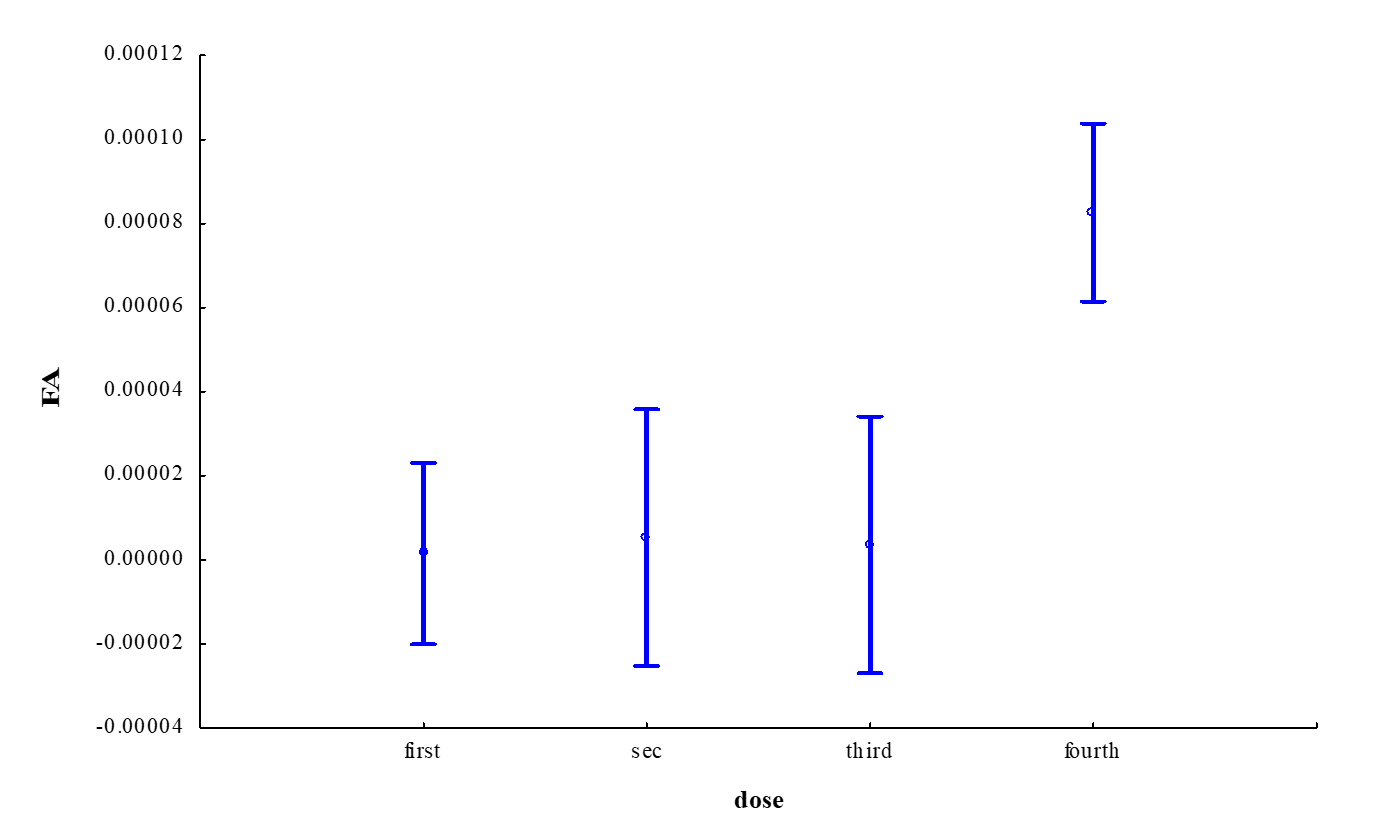
Рисунок 1 - Результаты однофакторного дисперсионного анализа по влиянию дозы удобрения на флуктуирующую асимметрию листьев озимой пшеницы (F(3; 148) = 12,16; p << 0,05)
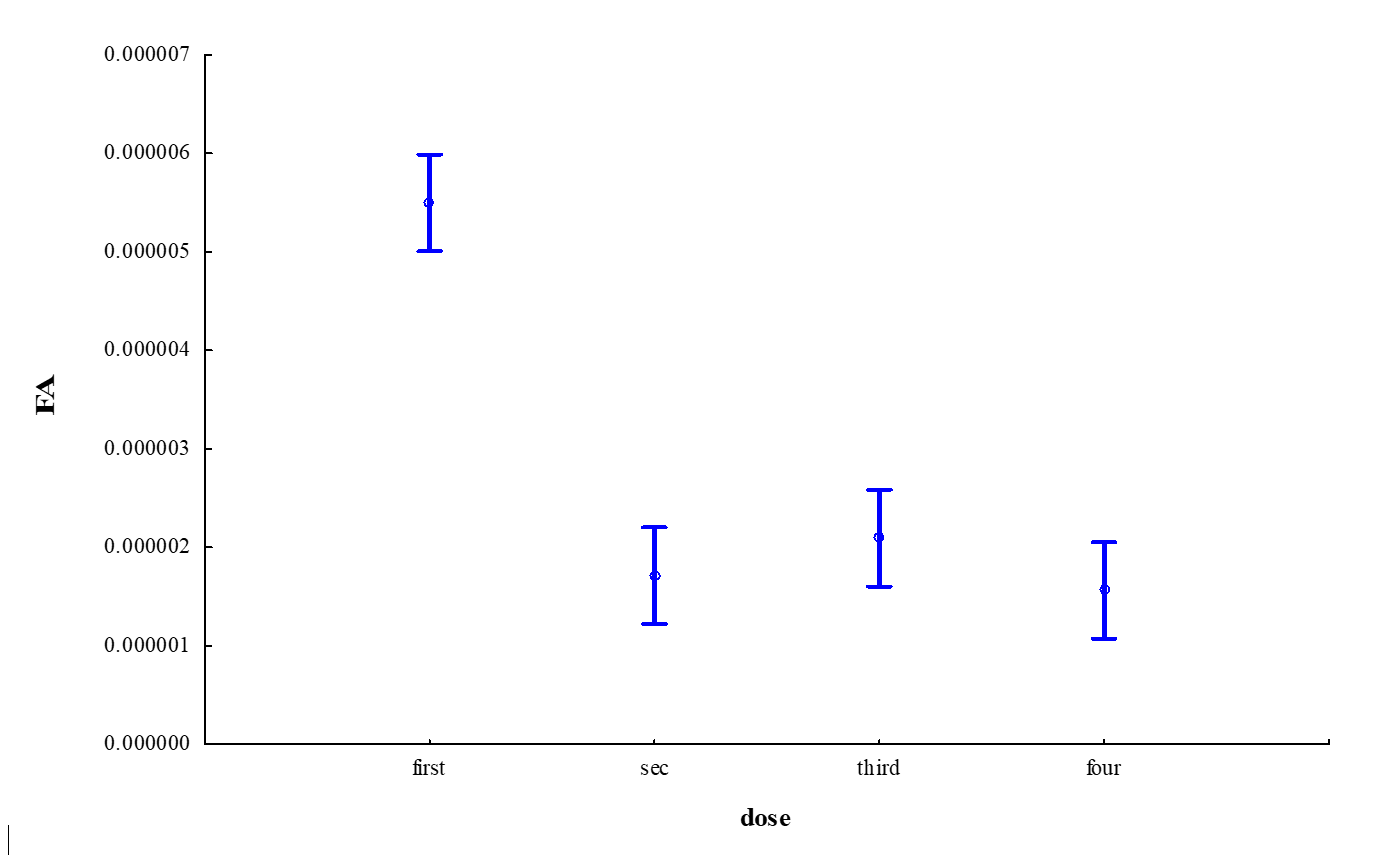
Рисунок 2 - Влияние дозы удобрения на флуктуирующую асимметрию листьев яровой пшеницы (F(3; 96) = 57; p << 0,05)
3.2. Моделирование
Озимая пшеница. В качестве категориальной переменной была выбрана доза вносимого удобрения (от 1-й до 4-й). Числовой переменной служили значения направленной асимметрии для каждой метки (всего 100 меток). Зависимой переменной служили значения ФА.
Был построен гнездовой план без взаимодействия эффектов, и использовалась опция «обобщенная линейная модель» (GLM, STATISTICA), позволяющая объединить различные модели распределения. Наиболее подходящая модель оказалась модель Твиди (TWEEDIE), относящаяся к экспоненциальному семейству моделей, связывающих дисперсию и среднее степенное. Была использована логарифмическая функция связи (link function). Регрессия ФА/НА показала близкие линии тренда, повышающиеся к 4-й дозе (ось ОХ; Рисунок 3).
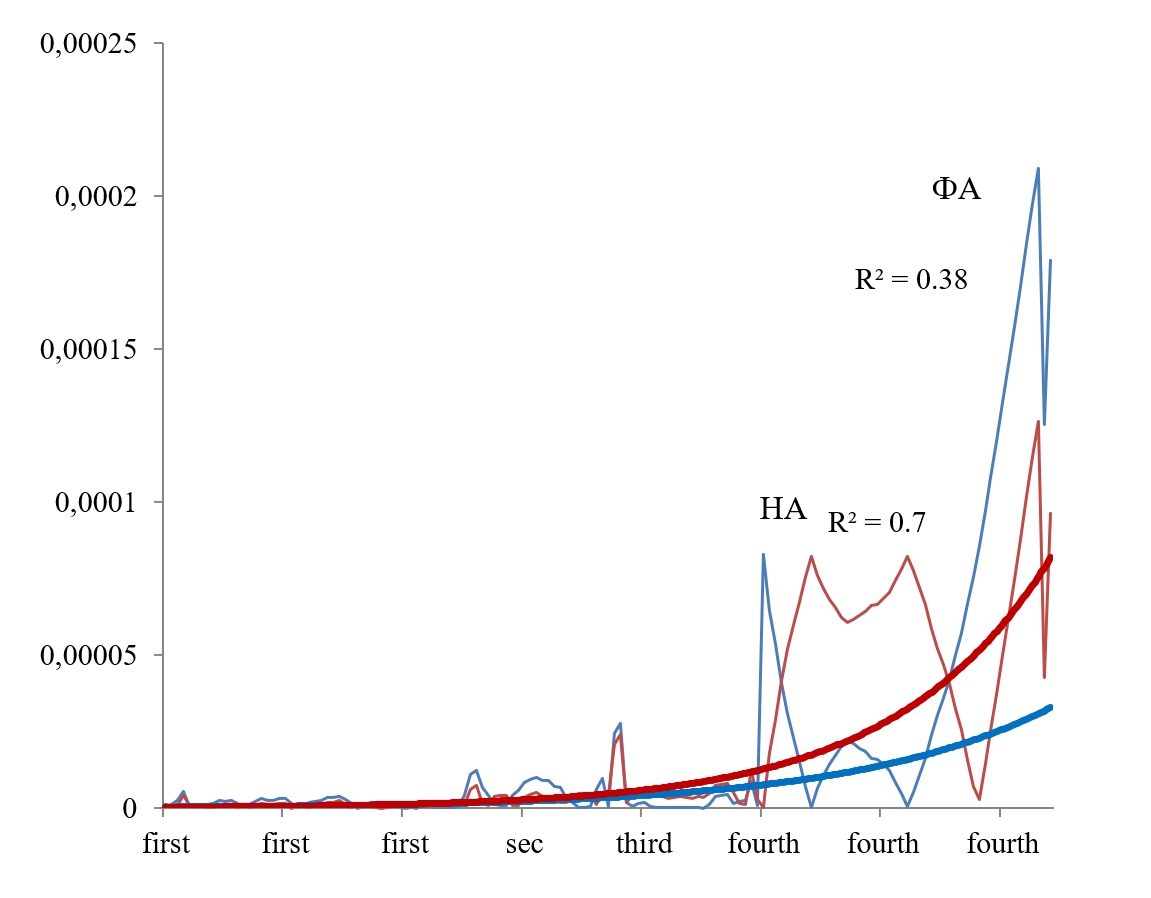
Рисунок 3 - Аппроксимационные линии тренда ФА (синяя линия) и НА (красная)
Примечание: Озимая пшеница, сорт Поэма, Excel
Яровая пшеница. Наиболее точная модель показала полиномиальное распределение оп фактору направленной асимметрии. Чем больше степень, тем выше была степень детерминации модели (на графике - пятая степень).
Полиномиальная регрессия статистически была значима только по R, но не по R2, например, фактор дозы был незначим (р > 0,05).
Общая регрессионная модель показывала высокую значимость R = 0,86. Был также применен тест Вальда (Wald) с нулевой гипотезой о равенстве нулю коэффициентов регрессии. Этот тест является асимптотическим, т.е. предназначенным для описания предельного поведения функций. Распределение Твиди показывало значимость только фактора направленной асимметрии – 15,7 р << 0,05), в целом модель была адекватной относительно направленной асимметрии (Рисунок 4).

Рисунок 4 - Аппроксимационные линии тренда ФА (синяя линия) и НА (красная)
Примечание: Яровая пшеница, сорт Грань, Excel
Другие виды распределения, например, логарифмическое нормальное, не подтверждали значимость коэффициентов регрессии, или подтверждали один из них, например по фактору дозы, на уровне 1-й, 2-й дозы.
Построенные линейные тренды свидетельствовали о различии двух сортов пшеницы в морфологии листовых пластин. У озимой пшеницы они были оформлены полностью как полноценный фотосинтезирующий орган растения, а время вегетации яровой было на два месяца короче, следовательно, ФА варьировала не так сильно, как в сорте озимой (Поэма).
4. Заключение
Стабильность развития была пониженной у озимой пшеницы (более высокая ФА) особенно, при четвертой высокоинтенсивной органоминеральной дозе. Мы считаем, что разные сроки вегетации (более короткая у яровой пшеницы) играют роль в стабильности развития. Отсюда – различные допустимые модели описывающие влияние генотипически зависимой направленной асимметрии и дозы удобрения на стабильность развития. Экспоненциальная модель была характерна для озимой. Полиномиальная, далекая от линейной – для яровой пшеницы. Авторы полагают, что моделирование стабильности развития представляет интерес при учете других факторов, климатических, а также факторов обработки почвы.
При разработке системы моделирования следует учитывать множество экспериментальных данных для получения системы, состоящей из набора модулей, например, использовать разработанные и описанные модели базовых процессов в специализированных программах .
Интерес представляет моделирование биометрических показателей в зависимости от сорта и влажности семян . При этом важно принимать во внимание модели флуктуаций не только асимметричности пластин, но и продуктивных показателей устойчивости агроэкосистем, как толерантности агроценоза к факторам среды .
