A MATHEMATICAL MODEL OF SINGLE POPULATION DISPERSAL

В экосистеме могут существовать популяции несколько видов разной численности. Области распространения видов сильно фрагментированы промышленной деятельностью человека и образуют небольшие зоны перекрывания. Поселения населений располагаются в различных антропогенно трансформированных ландшафтах с сильной деградацией участков обитания. Заселение особями популяции территории с неравномерно распределенными трофическими ресурсами сопровождается образованием отдельных зон обитания с различными объемами ресурса, его качеством, с различной численностью населения [1].

Распространение многих видов на территории носит выраженный очаговый характер. Относительно близких участков обитания различной емкости может быть от нескольких единиц до нескольких десятков. Плотность населения участков может отличаться в несколько десятков раз. Между участками через зоны перекрывания может происходить миграция особей [2], [3], [4], [5].

Важную роль в регуляции роста и размножения особей могут играть внутрипопуляционные, зависимые от плотности населения механизмы, связанные со стрессом. Социогенный стресс рассматривается как причина смертности и репродуктивной супрессии. В зависящих от плотности социальных средах могут запускаться регуляторные механизмы, ведущие к замедлению темпа размножения, созревания, обусловливающие смертность населения [6], [7].

Перемещения организмов в пространстве происходит по разным причинам. Это может быть активное перемещение многих видов животных и птиц, и пассивное перемещение под влиянием внешних факторов. Миграция сопровождается массовым перемещением особей конкретного вида из одного места обитания в другое. Расселение обусловлено удалением особей друг от друга из-за переселения или недостатка трофического ресурса. Переход может сопровождаться уходом только части особей из «материнского» участка, а убыль возмещается приходом особей с других участков. Расселение вызывается покиданием материнских участков, приводящим к уменьшению численности особей на перенаселенном месте обитания. Расселение жизненно необходимо для некоторых видов, поскольку способно снять проблему перенаселения [8].

Миграция и расселение относится к группам особей, в то время как перемещается отдельно каждая особь популяции. Групповое перемещение особей характеризуется привлекательностью группы особей к конкретным местам обитания [2].

При случайном размещении организмов любое место в среде обитание может быть занято организмом с равной вероятностью и не связано с присутствием других организмов. При групповом размещении особи привлекаются к определенным участкам среды обитания, или привлекаются другими особями популяции [8].

В основе математической модели лежит вариант расселения вида по разным, но близким, местам обитания. При этом предполагается, что динамика популяционного сообщества в конкретном месте обитания зависит от свойств среды обитания и внутренних регуляторных механизмов. То есть, рождаемость и смертность определяются трофическим ресурсом, а переход особей в соседние места обитания определяется поиском трофического ресурса или социогенными факторами [6].

Пусть среда обитания популяции состоит из n-зон различной емкости с различным трофическим ресурсом. Особям популяции доступна только часть трофического ресурса. Удельные скорости роста численности популяции в зонах различны. Часть особей популяции может перемещаться в две соседние зоны в равных долях, но различных для разных зон. В пограничных зонах переход возможен только в одну соседнюю зону. Трофический ресурс, потребляемый особями, восполняется в каждой зоне с разной удельной скоростью. При этих предположениях математическая модель расселения особей по зонам представлена задачей Коши для системы дифференциальных уравнений [9], [10]

(1)

где  ‑ численность особей популяции в -ой зоне ,  ‑ объем трофического ресурса в -ой зоне,  ‑ доля особей, покидающих -ю зону,  ‑ удельная скорость роста численности популяции в зоне , а  ‑ трофического ресурса,   ‑ емкость -ой зоны,  ‑ стационарная емкость трофического ресурса,  и  ‑ параметры. Условия  предполагают, что особи могут не покидать свою зоны, а в случае перемещения часть особей остается в материнской зоне.

Слагаемое  в уравнениях (1) для популяций – доля трофического ресурса в -ой зоне доступного для особей популяции. Слагаемое  в уравнениях для  ‑ скорость «поедания» трофического ресурса особями популяции.

К системе уравнений (1) добавляются начальные условия при . Первый вариант начального заселения одновременно всех зон малочисленными группами

(2)

где .

Второй вариант начальных условий

(3)

рассматривается как вселение особей в первую зону с последующим их последовательным расселением по остальным зонам.

Для обоих вариантов начальных условий предполагается, что при  

Для случая отсутствия перемещения особей из зоны в зону из системы уравнений (1) для -ой зоны следуют уравнения

(4)

Точки притяжения этой системы уравнений находятся из системы уравнений

(5)

Левая часть второго уравнения в (5) при  обращается в ноль, но является возрастающей функцией , а при  принимает отрицательное значение. Поэтому при  система уравнений (4) будет иметь решение. Оба собственных значения матрицы Якоби системы уравнений (4) в этой точке будут отрицательными. Соответственно эта стационарная точка будет устойчивой.

Стационарные точки ,  и ,  будут неустойчивыми.

Из системы уравнений (1) следует уравнение

(6)

Как следует из анализа этого уравнения при и малых значениях  правая часть этого уравнения будет положительной величиной. Поэтому при любом начальном заселении зон малочисленными группами популяции общая численность популяции будет увеличиваться.

Из уравнения (6) также следует, что при отсутствии трофического ресурса во всех зонах общая численность особей будет убывать.

Пусть особи популяции расселились в двух зонах. Для случая двух зон из (1) следуют уравнения динамики численности населения двух популяционных групп

В отсутствие миграции (при  и ) в стационарном состоянии

При начале перехода малых долей ( и ) особей из зоны в зону стационарные значения  и  изменяться на малую величину так, что

где  и .

При этом предполагается, что малым изменением трофического ресурса можно пренебречь.

С учетом этих предположений смещение стационарных точек в линейном приближении находятся из системы уравнений

Отсюда следует, что

(7)

где

.

Как следует из анализа соотношений (7) в линейном приближении уменьшается численность особей в той зоне, которую покидает большая часть особей.

Все зоны обитания групп особей популяции имеют разные трофические ресурсы, потребляемые особями, разные емкости среды, восстановление ресурсов может происходить с разными скоростями. Удельная скорость роста численности популяции зависит от качества трофического ресурса. Поэтому в рамках имитационной модели предполагается, что все параметры модели (1) могут отличаться от базовых значений не более, чем в три раза. Причем принимается, что отклонение носит случайный характер. Таким образом, принималось, что , , , , , . Параметры  соответствует периоду удвоения численности популяции от 3 до 8 месяцев, а параметры  ‑ периоду восстановления трофического ресурса от 12 до 36 месяцев. Выбор всех параметров выбирался случайным образом для каждой зоны отдельно.

На рис. 1 приведено распределение групп особей по численности в стационарном состоянии для случая 50 зон. За единицу принята максимальная численность из всех численностей в зонах. Распределения для начальных условий (2) и (3) отличаются не более чем на 2% в максимальных отклонениях. Для случая начальных условий (3) на рис. 2 приведено распределение групп популяций по времени начала заселения последней зоны из 10. За единицу принят наибольший промежуток времени достижения последней зоны. Как следует из анализа полученных результатов при увеличении параметров  () эти зависимости отличаются не более чем на 5% в максимальных отклонениях. На эти распределения практически не влияет и количество зон.

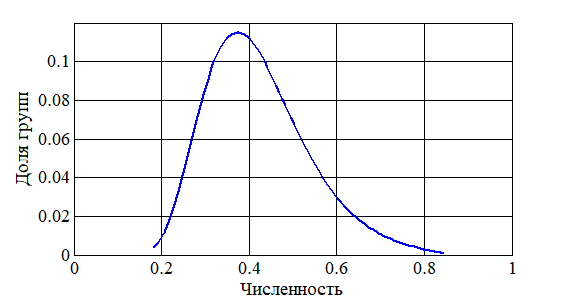
Рисунок 1 - Распределение мест обитания по численности населения

DOI:10.23670/IRJ.2022.124.11.1

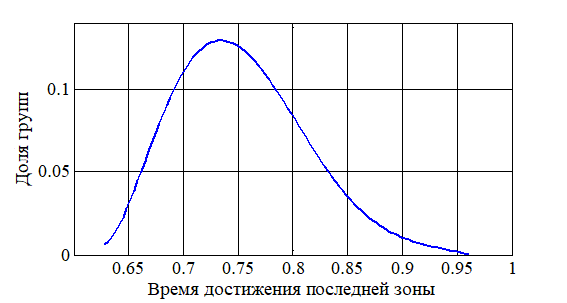
Рисунок 2 - Распределение групп популяций по продолжительности заселения территории

DOI:10.23670/IRJ.2022.124.11.2

Распределение зон по численности населения согласуются с данными полевых наблюдений за расселением птиц, приведенными в [8].

Фрагментирование человеком территории приводит и к фрагментации зон обитания по их размерам, по разнообразию трофических ресурсов и их объемам. Расселение особей вида по зонам сопровождается образованием групп зон с малой численностью населения и высокой численностью с отличием в несколько раз. Численность населения в большей части зон будет отличаться незначительно от средней численности населения. Полученные варианты распределения особей согласуются с расселением особей в ненарушенных человеком естественных ареалах.