ON THE SOLVING THE SECOND-ORDER VERHULST DIFFERENTIAL EQUATION WITH PERTURBED INITIAL CONDITIONS

О РЕШЕНИИ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ФЕРХЮЛЬСТА ВТОРОГО ПОРЯДКА С ВОЗМУЩЁННЫМИ НАЧАЛЬНЫМИ УСЛОВИЯМИ

Научная статья

Михеев А.В.*

ORCID: 0000-0001-5953-0346,

Санкт-Петербургский государственный электротехнический университет «ЛЭТИ», Санкт-Петербург, Россия

* Корреспондирующий автор (artem.v.miheev[at]gmail.com)

Аннотация

В данной работе рассматривается динамическая система, поведение которой описывается дифференциальным уравнением второго порядка, где фундаментальная система решений, состоящая из функций экспоненциального типа, заменена на ограниченные функции модели Ферхюльста. Исследуется вопрос зависимости поведения частного решения построенного дифференциального уравнения второго порядка от возмущения его начальных условий. Общий вид возмущения полагается имеющим вид многочлена второй степени, зависящего от вспомогательного параметра µ. Полученные результаты проиллюстрированы тестовым примером с конкретными численными данными и соответствующими им графиками. В качестве вспомогательных средств для проведения расчётов используются программные пакеты MathCAD и Wolfram Alpha.

Ключевые слова: модель Ферхюльста, дифференциальные уравнения, динамические системы, численное моделирование.

ON THE SOLVING THE SECOND-ORDER VERHULST DIFFERENTIAL EQUATION WITH PERTURBED INITIAL CONDITIONS

Research article

Mikheev A.V.*

ORCID: 0000-0001-5953-0346,

Saint Petersburg Electrotechnical University "LETI", Saint Petersburg, Russia

* Corresponding author (artem.v.miheev[at]gmail.com)

Abstract

The article examines a dynamical system whose behavior is described by a second-order differential equation where the fundamental system of solutions consisting of functions of exponential type is replaced by bounded functions of the Verhulst model. The author investigates the question of the dependence of the behavior of a particular solution of the constructed second-order differential equation on the perturbation of its initial conditions. The general form of the perturbation is assumed to have the form of a polynomial of the second degree, depending on the auxiliary parameter µ. The obtained results are illustrated by a test example with specific numerical data and corresponding graphs. The MathCAD and Wolfram Alpha software packages are used as auxiliary tools for performing calculations.

Keywords: Verhulst model, differential equations, dynamical systems, numerical modeling. Введение

При рассмотрении динамики процессов различной природы, таких как рост финансовых накоплений, увеличение численности колоний микроорганизмов, популяции людей и животных и т.д., наиболее эффективным инструментом является использование дифференциальных уравнений. Одна из первых моделей роста популяции была предложена еще в 1798 году австрийским демографом и экономистом Томасом Мальтусом. В своём фундаментальном труде «Опыт закона о народонаселении» [1] Мальтус выдвинул гипотезу, согласно которой неконтролируемый рост популяций всегда превосходит скорость роста источников, которые её поддерживают. Его предположение указывает на геометрическую прогрессию неконтролируемого роста популяции в сравнении с арифметической прогрессией роста источников питания.

В теории популяций уравнением Мальтуса называется уравнение вида

    (1) c решением экспоненциального типа    (2)

Интерпретируя решение уравнения (1), Мальтус утверждал, что в человеческом обществе существует абсолютный закон безграничного размножения особей. И поскольку рост численности человеческого общества опережает темпы роста продовольственных запасов, то, следовательно, неизбежна жестокая конкуренция среди людей за «место под солнцем»:

«Человек, появившийся на свет, уже занятый другими людьми, если он не получил от родителей средств к существованию и если общество не нуждается в его труде, не имеет никакого права требовать для себя пропитания, ибо он совершенно лишний на этом свете. На великом пиршестве природы для него нет прибора. Природа приказывает ему удалиться, и если он не может прибегнуть к состраданию какого-либо из пирующих, она сама принимает меры к тому, чтобы её приказание было произведено в исполнение» [1].

Однако из-за большой скорости возрастания экспоненциальной функции модель Мальтуса применима к описанию реальных процессов только на начальном промежутке времени. Экспоненциальное возрастание популяции не может продолжаться достаточно долго, так как увеличение плотности популяции приводит к росту сопротивления внешней среды и снижению рождаемости. В качестве выхода из положения бельгийским математиком, профессором Брюссельского университета Пьером Ферхюльстом в работе [2] была предложена модель, близкая к экспоненциальной при , вводящая «порог насыщения» – горизонтальную асимптоту . Функция (3) данной модели является решением дифференциального уравнения (4):

   (3)    (4)

Подробный исторический обзор возникновения и развития представлений Ферхюльста дан в работе [3]. В статье [4] рассматривается вопрос расчёта динамической системы, описываемой дифференциальным уравнением второго порядка, в котором фундаментальная система решений, состоящая из функций экспоненциального типа, заменена на ограниченные функции (5) из модели Ферхюльста

    (5)

удовлетворяющие начальным условиям  и ограниченные сверху горизонтальной асимптотой . Функции  составляют фундаментальную систему решений (ФСР) линейного дифференциального уравнения (ЛДУ) второго порядка с переменными коэффициентами:

    (6) При этом коэффициенты  выражаются через элементы ФСР по формулам (7):     (7) Где     (8)

Проанализирована временная зависимость сил, воздействующих на динамическую систему, и проведено сравнение полученной зависимости с экспоненциальным случаем.

В статье [6] автором была исследована зависимость поведения частных решений уравнения (6) от вида начальных условий

    (9)

Было проведено построение т.н. «областей гарантированной монотонности» на плоскости параметров начальных условий, для которых решение исходного уравнения строго возрастает (строго убывает). На основе общего алгоритма нахождения корней производной и промежутков монотонности были проанализированы различные примеры поведения решений рассматриваемого уравнения. Были обнаружены три вида решений: функции с двумя экстремумами, с одним экстремумом, а также монотонные функции.

В статье ([7]) рассматривался вопрос численного интегрирования дифференциального уравнения (6) с заданными начальными условиями вида (9). Для этой цели использовалось два вида приближенных вычислений: расчёты в программе MathCAD [8] и представление решения в виде ряда Тейлора в окрестности точки, соответствующей начальным условиям [9], [10]. На основе рассматриваемого тестового примера проводилось сравнение приближенных данных с точным решением уравнения. Полученные результаты были представлены в аналитической и графической формах.

Динамическая система с моделью Ферхюльста

В рассматриваемой модели будем полагать (см. [10]), что отклонение динамической системы от ее начального состояния обусловлено наличием двух сил:  «силы тяготения» и «силы сохранения» . Используя аналог закона Ньютона  и полагая , получаем ЛДУ второго порядка c двумя начальными условиями (10), описывающее поведение системы:

   (10)

В простейшем случае коэффициенты  являются постоянными. Из общей теории ЛДУ второго порядка [10] следует, что при  фундаментальная система решений (ФСР) состоит из двух функций экспоненциального типа  - корни характеристического уравнения. При дальнейших рассмотрениях будем считать, что . Каждое из частных решений уравнения (10) описывает поведение динамической системы во времени. Заменяя ФСР уравнения (10) на функции вида (5), мы получим новое уравнение вида (6) с переменными коэффициентами.

Цель данной работы – исследовать поведение частных решений уравнения (6) при возмущениях начальных условий (11), заданных в виде зависимостей:

    (11)

Предполагая, что начальная численность популяции зависит от расстояния до фиксированной отправной точки, мы можем задать эту зависимость при помощи параметра μ. Квадратичный вид этой зависимости в (11) представляет собой простейший тип нелинейности, пригодный для рассмотрения. Особый демографический смысл это имеет, например, при анализе численности населения в центре города и пригородных поселениях, сгруппированных вокруг общего центра, где имеется структура, близкая к характеристикам к центральной симметрии. 

Зависимость частного решения от начальных условий

Введём следующие вспомогательные обозначения:

    (12)

где  – множители экспоненциальных показателей (5), k – правая часть уравнения горизонтальной асимптоты, ограничивающей функции (5). В таком случае частное решение уравнения (6), удовлетворяющее возмущённым начальным условиям (11) может быть представлено в следующем виде:

   (13)

Поведение частного решения при возмущении начальных условий

Поскольку , каждое из решений вида (13) при фиксированном значении параметра μ имеет горизонтальную асимптоту вида . Согласно [6], в случае, если выполнена система неравенств

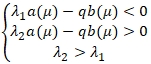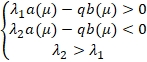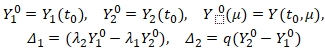   (14) функция  монотонно возрастает по параметру t, если же     (15) то функция  монотонно убывает по t. Теперь зафиксируем значение  и введём следующие обозначения:    (16) Тогда тождество (13) перепишется в виде:    (17) Разлагая (17) в ряд по параметру , получим:     (18) где    (19)  

Если  выражение (18) представляет собой линейную зависимость. Если , поведение данной функции определяется свойствами многочлена второй степени: при  функция  убывает на промежутке , имеет минимум в точке  и возрастает на промежутке . При  функция  возрастает на промежутке , имеет максимум в точке  и убывает на промежутке

Численное моделирование

Рассмотрим тестовый пример задачи со следующими значениями входящих в неё параметров: . На рисунке 1 приводится графическая зависимость

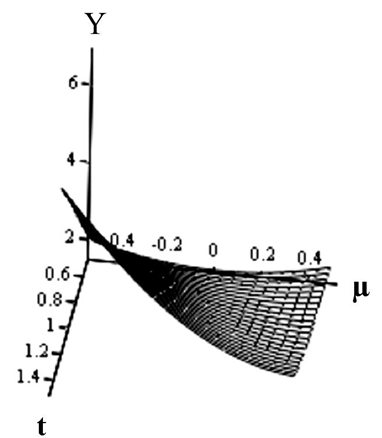
Рис. 1 – Графическая зависимость

 

На рисунке 2 отображены графики решений ЛДУ (6) с начальными условиями (11) при  с шагом 0.1. Все данные решения представляют собой монотонно возрастающие функции со значениями уровней горизонтальных асимптот, приведенными в таблице 1.

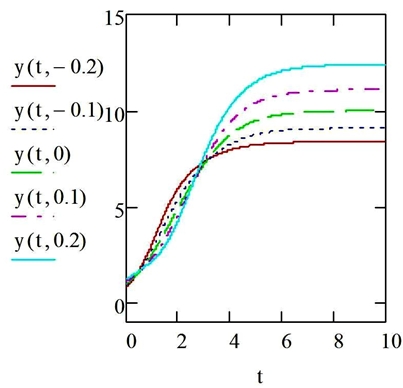
Рис. 2 – Графики решений ЛДУ (6) с начальными условиями (11) при  с шагом 0.1.

 

Таблица 1 – Значения уровней горизонтальных асимптот

µ	-0,2	-0,1	0	0,1	0,2
ka(µ)	8,4	9,1	10	11,1	12,4

 

Наконец, на рисунке 3 отображена зависимость  Мы видим, что она является квадратичной, как и было описано выше.

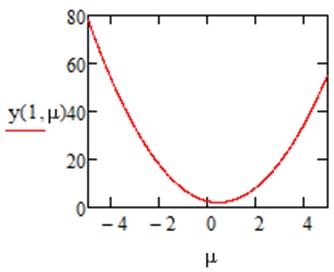
Рис. 3 – Зависимость 

  Заключение

Полученные результаты показывают, что частные решения уравнения (6) в зависимости от начальных условий могут включать себя функции как убывающего, так и возрастающего типа, ограниченные сверху горизонтальной асимптотой. В то же время зависимость частного решения от μ с фиксированным t имеет вид квадратичной функции. Явное выражение частного решения уравнения Ферхюльста через ФСР и начальные условия позволяет исследовать поведение данного решения при возмущениях начальных условий в любой требуемой точке.

Конфликт интересов Не указан.

Conflict of Interest None declared.

Список литературы / References

1. Мальтус Т. Опыт о законе народонаселення / Т. Мальтус, Кейнс, Ю. Ларин // Антология экономической классики. – М., 1993. – 134 с.
2. Verhulst P. F. Notice sur la loi que la population suit dans son accroissement / P. F. Verhulst // Corresp. Math et Phys. – 1838. – №10. – P. 113–121.
3. Московкин В.М. Пьер-Франсуа Верхульст – забытый первооткрыватель закона логистического роста и один из основателей экономической динамики / В.М. Московкин, А.В. Журавка // Наука та наукознавство. – 2003. – № 3. – С. 75-84.
4. Михеев А.В. О динамических моделях типа Ферхюльста, описываемых линейными дифференциальными уравнениями второго порядка / А.В. Михеев // Теория. Практика. Инновации. – 2017. – № 9 (21). – С. 29–33.
5. Романко В. К. Курс дифференциальных уравнений и вариационного исчисления / В. К. Романко. – 2-е изд. – М.: Лаборатория Базовых Знаний, 2001. – 344 с.
6. Михеев А.В. Исследование зависимости частных решений уравнения Ферхюльста второго порядка от начальных условий / А.В. Михеев // Теория. Практика. Инновации. – 2018. – № 8 (32). – С. 12–18.
7. Михеев А.В. О приближенном решении дифференциального уравнения Ферхюльста второго порядка / А.В. Михеев // Международный научно-исследовательский журнал. – 2019. – № 11-1 (89). – С. 17–20.
8. Кирьянов Д.В. Mathcad 15/Mathcad Prime 1.0 / Д.В. Кирьянов. – СПб.: БХВ-Петербург, 2012. – 432 с.
9. Данилина Н.И. Вычислительная математика / Н.И. Данилина, Н.С. Дубровская, О.П. Кваша и др. – М.: Высшая школа, 1985. – 472 с.
10. Панюкова Т.А. Основы теории дифференциальных уравнений для экономистов / Т.А. Панюкова. – М.: Кнжный дом «Либроком», 2011. – 256 с.

Список литературы на английском языке / References in English

1. Malthus T. Opyt o zakone narodonaselennja [An Essay on the Principle of Population] / Malthus T., Keynes, Larin Yu. // Antologija ehkonomicheskojj klassiki [Anthology of economic classics]. - M., 1993 – 134 p. [in Russian]
2. Verhulst P. F. Notice sur la loi que la population suit dans son accroissement / P. F. Verhulst // Corresp. Math et Phys. – 1838. – №10. – P. 113–121
3. Moskovkin V. M., Zhuravka A.V. P'er-Fransua Verkhul'st – zabytyjj pervootkryvatel' zakona logisticheskogo rosta i odin iz osnovatelejj ehkonomicheskojj dinamiki [Pierre-Francois Verhulst, the forgotten discoverer of the law of logistic growth and one of the founders of economic dynamics] / V. M. Moskovkin, A. V. Zhuravka // Nauka ta naukoznavstvo. - 2003. - No. 3. - pp. 75-84 [in Russian]
4. Mikheev A.V. O dinamicheskikh modeljakh tipa Ferkhjul'sta, opisyvaemykh linejjnymi differencial'nymi uravnenijami vtorogo porjadka [On dynamic models of the Ferhulst type described by linear differential equations of the second order] / A. V. Mikheev // Teorija. Praktika. Innovacii [Theory. Practice. Innovations]. – 2017. – № 9 (21). – pp. 29-33 [in Russian]
5. Romanko V. K. Kurs differencial'nykh uravnenijj i variacionnogo ischislenija [Course of differential equations and calculus of variations] / V. K. romanko – 2nd ed. - Moscow: Laboratorija Bazovykh Znanijj, 2001. - 344 p. [in Russian]
6. Mikheev A.V. Issledovanie zavisimosti chastnykh reshenijj uravnenija Ferkhjul'sta vtorogo porjadka ot nachal'nykh uslovijj [Investigation of the dependence of partial solutions of the second-order Ferhulst equation on the initial conditions] / A. V. Mikheev // Teorija. Praktika. Innovacii [Theory. Practice. Innovations] – 2018. – № 8 (32). – pp. 12-18 [in Russian]
7. Mikheev A.V. O priblizhennom reshenii differencial'nogo uravnenija Ferkhjul'sta vtorogo porjadka [On the approximate solution of the second-order Ferhulst differential equation] / A. V. Mikheev // Mezhdunarodnyjj nauchno-issledovatel'skijj zhurnal [International Research Journal]. – 2019. – № 11-1 (89). – pp. 17-20 [in Russian]
8. Kiryanov D. V. Mathcad 15/Mathcad Prime 1.0 / D. V. Kiryanov. - St. Petersburg: BKhV-Petersburg, 2012 – 432 p. [in Russian]
9. Danilina N. I., Dubrovskaya N. S., Kvasha O. P., Smirnov G. L. Vychislitel'naja matematika [Computational mathematics] / N. I. Danilina, N. S. Dubrovskaya, O. P. Kvasha. - M.: Vysshaya shkola, 1985. - 472 p. [in Russian]
10. Panyukova T. A. Osnovy teorii differencial'nykh uravnenijj dlja ehkonomistov [Fundamentals of the theory of differential equations for economists] / T. A. Panyukova. - M.: Knzhny dom "Librokom", 2011 – 256 p. [in Russian]