TRENING PROCESS EFFICIENCY IMPROVEMENT BY MATHEMATICAL MODELLING METHODS

Тишина Е.М.

Старший преподаватель кафедры «Начертательная геометрия и графика» Пензенского университета архитектуры и строительства

ПОВЫШЕНИЕ ЭФФЕКТИВНОСТИ ПРОЦЕССА ОБУЧЕНИЯ МЕТОДАМИ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ

Аннотация

В статье Е.М. Тишиной представлены результаты рассмотрения проблемы применения математических методов при моделировании учебного процесса. Проанализированы последние исследования и публикации по данной теме. Обоснована целесообразность использования методов математического моделирования. Построена логическая структура процесса обучения, учитывающая основные законы и принципы дидактики.

Ключевые слова: обучение, моделирование, технология учебного процесса, дидактические приемы и методы.

Keywords: training, modeling, technology of educational process, didactic receptions and methods.

Реформирование современного образования, его интеграция в европейскую и мировую систему, возрастающие требования к качеству подготовки специалистов различного профиля, обуславливают актуальность и важность постановки и решения задачи исследования методов и технологий повышения эффективности процесса обучения.

Высшие и средние специальные учебные заведения призваны, осуществлять подготовку кадров высокой квалификации, обладающих глубокими теоретическими знаниями, твердыми практическими навыками, способных решать сложные научно-технические вопросы. Это влечет разработку методик, повышающих качество обучения [1, 2].

Анализ теоретических и практических нововведений существующих методик обучения, позволяет выделить общие характерные признаки основных технологий обучения. В опубликованных работах представлены: программы для общеобразовательных и специальных учреждений; методики проведения занятий, приведены примерные списки практических работ (для каждого уровня усвоения). Перечень тем полностью соответствует содержанию общеобразовательного стандарта. Предложенные методики построены на основе дидактического усовершенствования и реконструкции учебного материала. Предлагая определенную методику проведения занятий, авторы четко формулируют цели и задачи, подробно описывают этапы их проведения, делая методические акценты на наиболее сложных и интересных аспектах учебного материала и процесса обучения. Дается примерное содержание заданий на дом.

В исследованиях и публикациях по этой проблеме недостаточно освещены вопросы, касающиеся повышения эффективности процесса обучения различными методами. Представлены методики, ориентированные на предметную ситуацию и не учитывающие контингент людей, ее реализующих. В рассмотренных работах отсутствует описание способов формализации процесса, создания универсальной методики обучения графическим дисциплинам.

Для повышения эффективности процесса обучения необходимо использовать методы математического моделирования. Подобный подход предполагает выявление входных и выходных параметров, определяющих структуру и качество функционирования учебного процесса. Кроме этого, требуется построить логическую структуру процесса обучения, учитывающую основные дидактические законы и принципы. Разработать оптимальную методику обучения, базирующуюся на предложенной математической модели.

Процесс обучения развивается во времени и имеет определенную последовательность действий, которая воплощается в конкретных формах и протекает по соответствующим правилам, называемыми законами дидактики. Логика этого взаимоотношения представлена графом на рис.1, где: 1. процесс обучения; 2. Законы дидактики; 3. Алгоритм; 4. Формы реализации алгоритма [3].

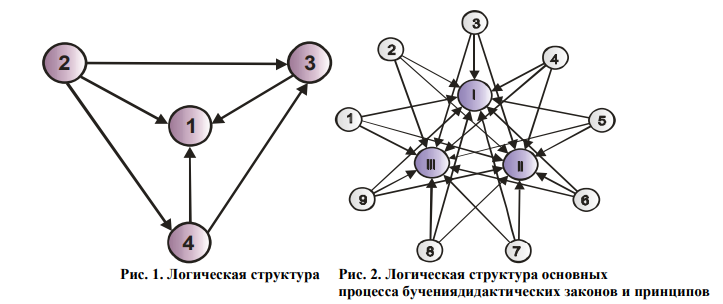
Для конкретизации логической структуры, каждой из выделенных вершин, необходимо рассмотреть: основные законы дидактики, алгоритм  процесса обучения и формы его реализации.

Дидактические концепции или системы представляют собой совокупность элементов, объединенных общими законами, принципами и образующих единую структуру, называемую процессом обучения.

Логическая структура основных дидактических законов и принципов представлена в виде графа (рис. 2), вершинами которого являются: I – закон социальной обусловленности обучения; II – закон обратной связи; III – закон целостности и единства обучения, 1) принцип природосообразности, 2) принцип непрерывности обучения; 3) принцип экологичности обучения; 4) принцип систематичности обучения; 5) принцип наглядности обучения; 6) принцип доступности обучения; 7) принцип прочности обучения; 8) принцип научности обучения; 9) принцип связи обучения с практикой [3].

Важным аспектом, характеризующим процесс обучения, является реализующий его алгоритм, состоящий из нескольких обязательных этапов, каждый из которых имеет свою цель. Целью первого этапа является подача новой информации. На втором этапе она усваивается, превращаясь в знания. Следуя принципу обратной связи, на третьем этапе необходим контроль качества знания. После этого наступает этап оценки проконтролированных знаний. Завершает эту процедуру этап коррекции [3].

Исходными параметрами математической модели учебного процесса являются: обучаемость студентов; квалификация педагога; материально-техническое обеспечение учебного процесса; логическая структура учебного курса, а выходным параметром служит – обратная связь.

В результате исследования выявлены взаимоотношения этих показателей. И в частности, между: квалификацией педагога – обучаемостью студентов, логической структурой учебного курса – квалификацией педагога, материально-техническим обеспечением учебного процесса – обучаемостью студентов, материально-техническим обеспечением учебного процесса – квалификацией педагога, материально-техническим обеспечением учебного процесса – логической структурой учебного курса, логической структурой учебного курса – обучаемостью студентов.

Таким образом, увеличение эффективности процесса обучения методами математического моделирования обеспечивается посредством аналитических исследований совокупности характеристик: обучаемость студентов; квалификация педагога; материально-техническое обеспечение учебного процесса; логическая структура учебного курса и категории «Обратная связь», приводящих к созданию математической модели. Проведенные исследования и установленные взаимосвязи дают возможность разработать алгоритм реализующий процесс обучения, повышающий эффективность, состоящий из подачи информации, усвоения знаний, использования обратной связи и контроля знаний.