SIMULATION OF THE SEISMIC WAVES GENERATED BY MOVING TRANSPORT

Заславский Ю.М.¹, Заславский В.Ю.²

¹с.н.с., д.ф.-м.н.; ²к.ф.-м.н. Институт прикладной физики Российской академии наук

МОДЕЛИРОВАНИЕ СЕЙСМИЧЕСКИХ ВОЛН, СОЗДАВАЕМЫХ ДВИЖУЩИМСЯ ТРАНСПОРТОМ

Аннотация

Проводится теоретический анализ сейсмических волн техногенной природы, генерируемых объектами транспорта, в частности, при их резком ускорении, или торможении, а также за счет воздействия на поверхность колеса, огибающего при движении дорожные неровности. Для моделирования транспортной сейсмики используются известные решения задачи анализа поверхностных волн Рэлея в однородном упругом полупространстве, возбуждаемых движущимся по его границе телом, создающим переменное силовое воздействие на горизонтальную поверхность. Предлагаемый анализ представляет интерес в решении проблемы выявления и исследования техногенных источников, порождающих тряску городских зданий, промышленных сооружений и объектов энергетики.

Ключевые слова: техногенная, транспортная сейсмика, поверхностные рэлеевские волны, упругое полупространство, воздействие на грунт, движущийся транспорт

Keywords: anthropogenic, transport seismicity, surface Rayleigh waves, elastic halfspace, impact on the ground, moving transport

Введение

Проблема борьбы с акустическим атмосферным шумом и с вибрацией жилых зданий и сооружений, порождаемымых движущимся транспортом, на территориях мегаполисов становится все более актуальной. Для ее решения требуется мониторинг характеристик акустического шума и «сейсмической активности» техногенной природы, а также исследование физических причин или источников шума и вибрации.

Исследования акустического атмосферного шума выполняются с начала прошлого века и продолжаются сейчас [1]. Они направлены на выявление источников, на отыскание способов снижения его негативного влияния, однако вопросы анализа сейсмовибрации затронуты пока в меньшей степени. В этой связи далее излагается теоретический анализ некоторых источников «транспортной» сейсмики, который может быть полезным для прогноза характеристик сейсмических колебаний, возбуждаемых движущимися объектами транспорта. В работе анализируются две модели возбуждения сейсмических волн: – за счет резкого торможения или ускорения массивных транспортных объектов; – вследствие взаимодействия ходовой части с неровностями профиля полотна дороги.

Первая модель возбуждения сейсмических колебаний

Рассмотрим случай, в котором происходит возбуждение сейсмической волны под действием силы трения между внешней поверхностью колеса и дорожным полотном (рис.1). Эта сила, действуя в течение некоторого промежутка времени, вызывает равнозамедленное движение тела (объекта транспорта массы 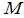), имеющего начальную скорость 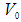, линейно спадающую до 0. Наибольший вклад в сейсмический отклик вносит поверхностная волна Рэлея [2], в связи с чем именно последняя берется в расчет. Излучаемая таким источником рэлеевская волна, имеет максимальную амплитуду в направлении параллельном ускорению 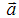(замедлению) или скорости тела  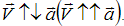Предполагаем, что постоянная по величине и направлению сдвиговая сила, равная 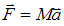, действует на ровную горизонтальную поверхность – границу твердой среды в течение времени 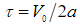. Кроме того, предполагаем, что точка воздействия – любая точка на отрезке от  до 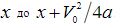. Используя предположение о действии этой силы в точке 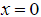, можно описать упругое волновое поле, излученное в виде импульса рэлеевской волны той же длительности . Аппроксимируем зависимость силы воздействия от времени колокольной (Гауссовой) функцией:

Тогда для спектра силы имеем следующую зависимость:

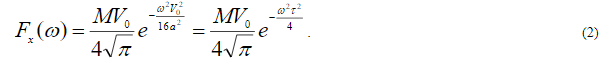
Известно [3, 4], что компоненты рэлеевской волны 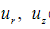(  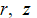– цилиндрические координаты) при гармоническом воздействии сдвиговой силой частоты  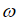и амплитудой  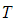, направленной вдоль  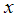и приложенной к точке на границе 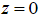, описываются формулами (фактор  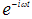опущен):

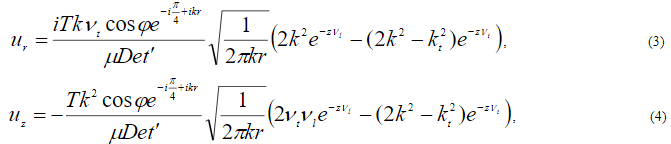
где 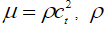, – плотность твердой среды, 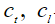– скорости поперечных и продольных волн, 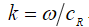– корень уравнения  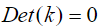– волновое число, соответствующее волне Рэлея,

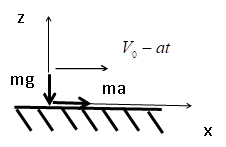
Рис.1. Схема воздействия на границу при торможении

 

 

а 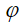 – угол азимута, отсчитываемый от направления вектора силы .

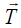Формулы (3), (4) описывают наличие азимутальной направленности в отклике рэлеевской волны, возбуждаемой горизонтальным сдвиговым воздействием. При этом для колебательного смещения 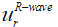 точек на границе  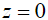в рэлеевской волне, возникающей при указанном гармоническом сдвиговом воздействии, справедлива формула:

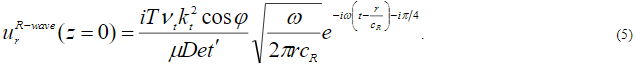
В рассматриваемом случае следует принять во внимание присутствие широкого спектра частот у воздействия (2), что приводит к следующему выражению для осциллограммы волнового отклика (после «двустороннего» интегрирования по частоте ):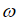

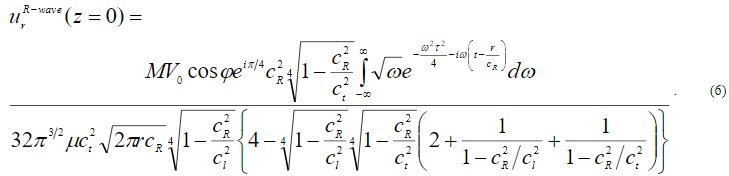
Качественный характер зависимости сейсмического отклика от времени (при учете только поля рэлеевской волны) представлен знакопеременной функцией на рис.2. При численном интегрировании 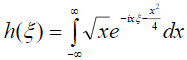 используется безразмерная частота  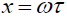и безразмерное время 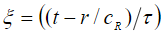. Если задаться характерным временем торможения 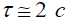, то из рис.2 следует, что длительность отклика составляет 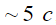, а следовательно, максимум в спектре излучаемого импульса приходится на . 

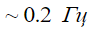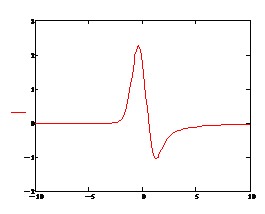
Рис.2. Сейсмический отклик

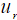(-компонента смещения в рэлеевской волне) на импульсное воздействие при торможении

Вторая модель возбуждения сейсмических колебаний

Далее рассмотрим другую модель возбуждения поверхностных сейсмических волн Рэлея, в основе которой лежит волновое возбуждение подрессоренным колесом автомобиля, действующим на поверхность грунта вертикальной переменной силой, возникающей при качении по неровностям. Для расчета спектра силы необходимо предположить, что качение происходит с постоянной горизонтальной скоростью 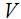, имеет место безотрывное огибание рельефа неровностей границы 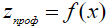, так что вертикальные хаотические колебания колеса при качении являются причиной появления переменной силы, действующей на грунт (рис.3). Причем поступательная скорость не может быть высокой  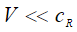и это обстоятельство исключает необходимость учета доплеровского эффекта. Переменная сила, как и зависимость от времени сейсмического поля, будет иметь вид случайной функции. Вместе с тем, для дальнейшего анализа поля поверхностной волны Рэлея используется предположение об идеально гладкой горизонтальной границе, вдоль которой происходит распространение волны по разным направлениям.

В расчетах ограничимся учетом вертикально направленной компоненты силы, а также пренебрежем вкладом сил, возникающих из-за реакции упругой подвески колеса на перемещения центра колеса при его качении по неровностям. 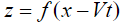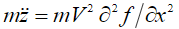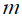Вследствие качения колеса, пространственная зависимость профиля преобразуется во временную зависимость движения центра колеса по формуле , а вертикальная компонента силы на грунт в наших предположениях определится как где – масса колеса.

Зададимся спектром мощности 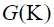 функции  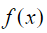следующего вида [5]:

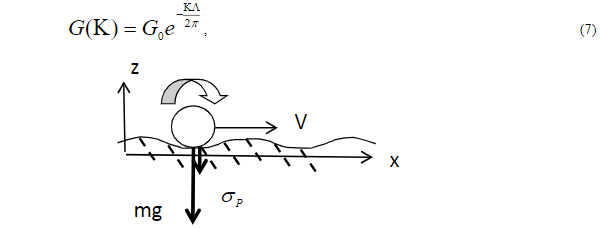
Рис.3. Схема воздействия колеса на неровную поверхность при безотрывном качении

где 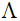– характерная длина неровностей дорожного покрытия, 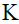– пространственная частота спектра неровностей профиля.

Дисперсия неровностей на границе определяется как 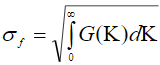.  Принимая для оценок 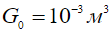, характерную длину неровностей дорожного покрытия 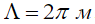. а также после интегрирования с учетом (7) 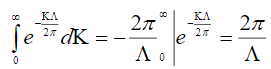, для дисперсии неровностей получаем

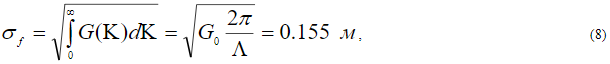
что соответствует дорожному покрытию грунтовой проселочной дороги [5].

Спектр мощности переменной силы 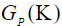 выражается через спектр неровностей :

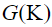Оценка дисперсии вертикально направленной переменой силы на грунт выполняется на основе формулы:

 

После интегрирования 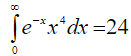 нетрудно придти к выражению для дисперсии переменной силы, действующей на поверхность грунта со стороны каждого колеса при условии безотрывного качения по полотну дороги:

При массе колеса 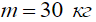 и выбранном спектре неровностей (7) предельно допустимая скорость качения, вероятно, составит  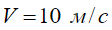(или близка к ней), а при более высоких его значениях условие безотрывности качения нарушается, ибо дисперсия силы превысит вес колеса. Оценка дисперсии силы по формуле (11) дает величину .

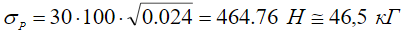Формула для смещения 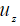 в рэлеевской волне, вызванной действием осциллирующей вертикальной переменной силы с амплитудой  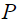 и частотой 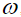, аналогичная (5), следующая:

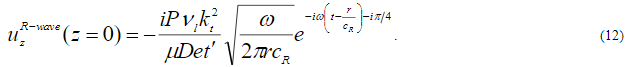
Выражение (12) является исходным для получения спектра мощности волновых перемещений, рассматриваемых как бесконечный случайный процесс. Этот спектр может быть выражен либо в виде функции временной частоты 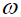, либо пространственной частоты 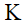, причем следует учесть наличие связи . 

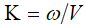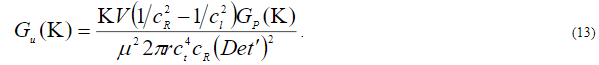
Раскрывая 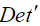и 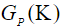, приходим к формуле для спектра мощности волновых смещений в зависимости от ,:

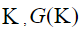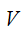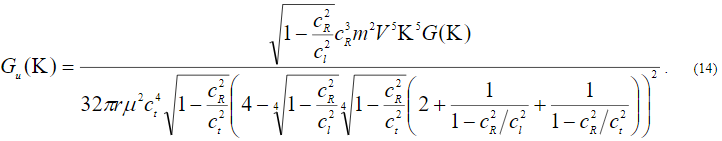
Для учета волнового поглощения при распространении в грунте необходимо в спектр мощности ввести фактор экспоненциального затухания сейсмической поверхностной волны  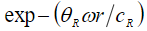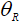–  ( декремент затухания) [6]. Принимая во внимание соотношения 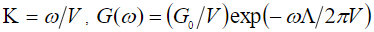, нетрудно получить формулу для спектра, как функции частоты 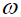, позволяющей построить график спектра, а также  получить оценки уровня: 

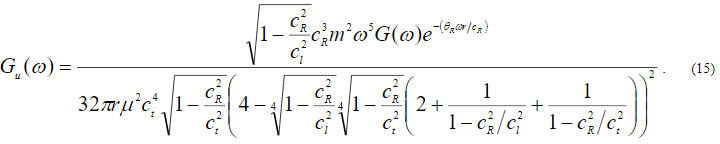
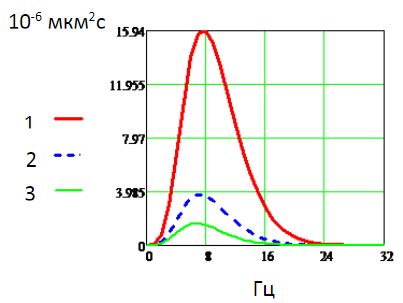
Рис.4. Спектр мощности волновых смещений на дистанциях 1 –10 м, 2 –30 м, 3 –50 м от источника

На рис.4 представлены спектры мощности волнового отклика для нескольких дистанций от источника 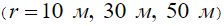 при 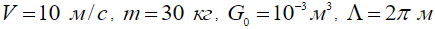 и применительно к случаю неконсолидированного, рыхлого грунта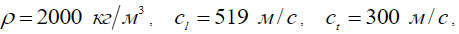 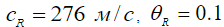. На столь малых удалениях, какие рассмотрены выше, влияние фактора поглощения волн незначительно, но его роль существенно возрастает для дистанций, больших 200 м. Нетрудно видеть, что вблизи источника максимум спектра приходится на частоту вблизи 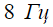, но по мере увеличения дистанции имеет место резкое падение спектральной плотности и сдвиг максимума спектра к низким частотам. Наконец, наличие у автомобиля нескольких колес приведет к некогерентному суммированию спектральной плотности мощности сейсмооткликов на воздействие каждым колесом.

Выводы

Таким образом, при сравнении частот спектральных максимумов, соответствующих рассмотренным двум моделям, становится очевидно, что вторая модель более высокочастотна. Можно также отметить, что если акустическое излучение транспортных шумов в воздухе соответствует диапазону нижних и средних звуковых частот, то техногенные сейсмические колебания занимают интервал инфразвуковых частот от десятых долей герца до нескольких первых десятков герц. Несмотря на то, что представленные иллюстрации получены в результате частного выбора параметров, с помощью выведенных формул нетрудно прогнозировать характеристики сейсмических откликов применительно к другим количественным значениям исходных параметров полотна дороги, объектов транспорта и среды.