SIMULATION OF ELECTRO-OPTICAL PROCESSES IN THE DIODE, BASED ON N +-SI/ N-SI:ER/ P +-SI STRUCTURE UNDER THE REVERSE BIAS AND WAYS TO IMPROVE THE RELIABILITY OF MODELING AGENCIES

Зимовец И. А.¹, Филатов Д. О.²,

¹аспирант ННГУ; к.ф.-м.н., ²доцент, НОЦ ФТНС ННГУ,

МОДЕЛИРОВАНИЕ ЭЛЕКТРОННО-ОПТИЧЕСКИХ ПРОЦЕССОВ В ДИОДЕ НА ОСНОВЕ СТРУКТУРЫ N +-SI/ N-SI:ER/ P +-SI ПРИ ОБРАТНОМ СМЕЩЕНИИ И ПУТИ ПОВЫШЕНИЯ ДОСТОВЕРНОСТИ МОДЕЛИРОВАНИЯ СТРУКТУР

Аннотация

Развита математическая модель, описывающая процессы возбуждения электролюминесценции ионов Er³⁺ в диодах на основе структуры n⁺-Si/n-Si:Er/p⁺-Si при обратном смещении. Модель учитывает процессы туннельной инжекции электронов из валентной зоны слоя p⁺-Si на глубокие уровни, связанные с примесью Er в активном слое n-Si:Er.

Ключевые слова: моделирование, электронно-оптические процессы, диод.

Keywords: modelation, electron optic process, diod.

В большинстве работ по эрбиевой электролюминесценции (ЭЛ) в структурах Si/Si:Er/Si с p—n переходом в режиме пробоя при обратном смещении для объяснения наблюдаемых эффектов предполагается, что возбуждение ЭЛ на длине волны l » 1,54 мкм в 4f-оболочке ионов эрбия обусловлено передачей им энергии горячими электронами зоны проводимости. Требуемую энергию (не менее 0,8 эВ) электроны могут набирать при взаимодействии с электрическим полем в области пространственного заряда (ОПЗ) p—n перехода. Однако, как показано в работе [1], такая модель содержит противоречия с результатами экспериментов. Там же предложена качественно новая модель, основанная на предположении, что возбуждение излучательных переходов в 4f-оболочке ионов эрбия обусловлено передачей им энергии, освобождаемой в результате безызлучательных переходов электронов с глубоких донорных состояний, образуемых комплексами эрбия в запрещенной зоне кремния, на нейтральные мелкие акцепторы (B, Al или Ga) с концентрацией на уровне ~ 10¹⁷ см^‑3 в слоях Si:Er, выращенных методом сублимационной молекулярно-лучевой эпитаксии (СМЛЭ). Такая модель хорошо применима для качественного объяснения наблюдаемых экспериментальных эффектов, но ряд ее положений требует доказательств.

Диффузионно-дрейфовая модель диода в стационарном состоянии состояла из пяти уравнений фундаментальной системы уравнений физики полупроводников (ФСУ) — стационарных уравнений непрерывности для электронов и дырок и уравнения Пуассона, которые задают взаимосвязь между пятью основными характеристиками диода :концентрации электронов и дырок, дырочный и электронный токи, также напряженность электрического поля. Зонная диаграмма перехода p⁺-Si/n-Si:Er рассчитывалась на базе решения уравнения Пуассона:

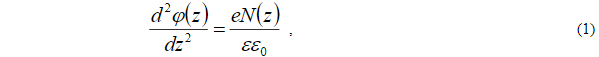
где 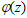—профиль потенциаладля электронов, 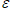—диэлектрическая проницаемость Si, 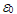—диэлектрическая постоянная, е—элементарный заряд,

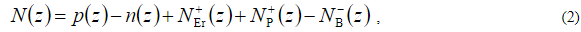
—концентрация дырок в валентной зоне, Nv—эффективная плотность состояний в валентной зоне Si, Fp—квазиуровень Ферми для дырок, 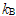—постоянная Больцмана, Т—абсолютная температура,

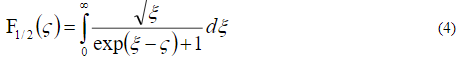
—интеграл Ферми порядка ½,

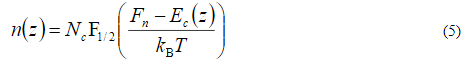
—концентрация электронов в зоне проводимости, 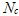—эффективная плотность состояний в зоне проводимости Si, 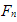—квазиуровень Ферми для электронов В этом случае решение уравнения Пуассона: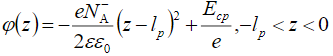 

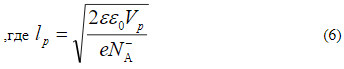
— толщина части ОПЗ, приходящаяся на слой p⁺-Si, V_p — доля контактной разности потенциалов р⁺—n перехода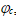 падающая на ОПЗ слоя p⁺-Si  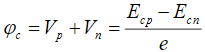  ,     где V_n — доля 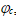падающая на части ОПЗ, лежащей в слое n-Si:Er, E_cp и E_cn — энергии дна зоны проводимости в квазинейтральных областях слоёв p⁺-Si и n-Si:Er (области I и IV, соответственно). На границе квазинейтральной области слоя n-Si:Er (z = l_n) условие квазинейтральности записывалось в виде: 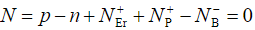,что даёт

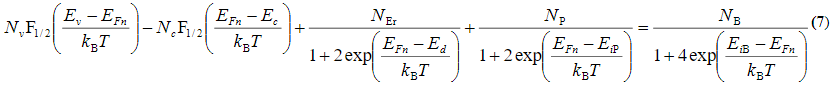
Рассматривался процесс туннельной инжекции электрона из валентной зоны на глубокий центр с координатой 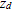 Форма потенциальной ямы глубокого центра аппроксимировалась водородоподобной моделью:

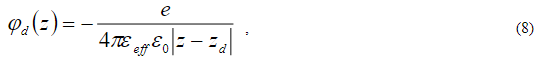
где e_eff = (R_y/E_d)^1/2 — эффективная диэлектрическая проницаемость, R_y 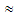 13,6 эВ — потенциал ионизации атома водорода (постоянная Ридберга).

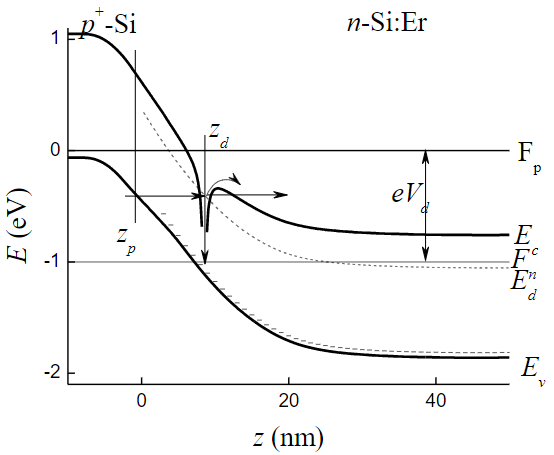
Рис. 1. Расчётная зонная диаграмма структуры p⁺-Si/ n-Si:Er (300К) при приложении обратного смещения V_d = 1 В. N_Er = 3×10¹⁸ cм^–3, E_d = 0,3 эВ

Все уравнения модели являются дифференциальными уравнениями первого порядка в частных производных. Модель требует постановки пяти граничных условий. В литературе методы, посвященные моделированию полупроводниковых структур предлагают задавать граничные условия следующим образом: четыре условия получаются фиксированием концентраций дырок и электронов на обеих контактах структуры, в качестве пятого условия берется равенство разности потенциалов но границах и интеграла от напряженности  поля. Иногда полагается равной нулю напряженность поля на границах ( полагается , что вне структуры , в металле ,падение напряжения мало, по сравнением с падением его в диоде), накладываются упрощающие ограничения на токи, пятое, интегральное условие при этом сохраняется. Однако при использовании этих условий возникает проблема несовместимости граничных условий с самой системой – когда уравнение наряду с диссипативным членом содержит и конвективный, что сильно усложняет задачу численного интегрирования. Модель структуры приходится применять либо в слоистых средах, в которых свойства материалов меняются скачкообразно, либо в средах с непрерывно, но очень быстро меняющимися свойствами. Сами величины, участвующие в модели могут иметь большие градиенты. это приводит к трудностям в построении устойчивого алгоритма  численного решения, точное решение может быть не гладким или не непрерывным, что требует применения надежных численных методов.

При решении системы дифференциальных уравнений в частных производных использовалось расширение математического пакета Matlab – пакет FEMLAB. При решении систем дифференциальных уравнений в частных производных система FEMLAB использует метод конечных элементов. Программное обеспечение выполняет конечноэлементный анализ вместе с адаптивным построением сетки, используя целый ряд численных решателей. Большой  интерес представляет реализация в среде FEMLAB новый тип разностных схем – бикомпактные схемы. Решение задач в слоистых средах сложно тем, что трудно построить аппроксимацию, дающую высокий порядок точности на стыках сред. Если задавать сетку так, что граница сред лежит между узлами сетки, то построить аппроксимацию сложно, и приходится выбирать сетку так, чтобы ее узлы попадали на границы слоев (такие сетки называются специальными). Если шаблон аппроксимации  содержит три и более пространственных узла, то специальные сетки не спасают - если внутренний узел шаблона совпадает с границей, то аппроксимация производных идет через разрыв коэффициентов- ухудшается точность расчетов.  Использование в расчете полуцелых узлов приводит к такому же эффекту. Использование бикомпактных схем (шаблон состоит из двух узлов сетки, полуцелые точки в расчетах не участвуют) позволяет достигнуть высокой точности расчета.