EXCEL SOLVER AS CURE OF TASKS OF THE THEORY OF GAMES

Гришкина Т.Е.¹, Лебедь О.А.¹, Лебедь О.А.¹

¹старший преподаватель, ФГБОУ ВПО «Амурский государственный университет»

ПОИСК РЕШЕНИЯ КАК СРЕДСТВО РЕШЕНИЯ ЗАДАЧ ТЕОРИИ ИГР

Аннотация

В статье рассматривается  пример решения задачи по теории игр с использованием надстройки «Поиск решения» электронных таблиц Microsoft Excel с целью оптимизации процесса обучения.

Ключевые слова: Поиск решения,  Microsoft Exсel, теория игр.

Keywords:  Excel Solver, Microsoft Exсel, theory of games.

Развитие информатизации образования и внедрение в учебный процесс современных информационных технологий повышает эффективность и качество обучения; обеспечивает мотивацию к самостоятельной познавательной деятельности студентов; способствует углублению межпредметных связей за счет интеграции информационной и предметной подготовки.

Надстройка «Поиск решения» представляет собой мощный инструмент для выполнения сложных вычислений, позволяет находить значения переменных, удовлетворяющих указанным критериям оптимальности, при условии выполнения заданных ограничений. Такие результаты оптимизации оформляются в виде отчетов трёх типов: результаты, устойчивость и пределы.

Использование надстройки «Поиск решения» дает преимущество в решении социально-экономических  задач, в которых необходимо принимать решения в условиях неопределенности, т. е. возникают ситуации, в которых две (или более) стороны преследуют различные цели, а результаты любого действия каждой из сторон зависят от мероприятий партнера. Такие ситуации относятся к конфликтным: результат каждого хода игрока зависит от ответного хода противника, цель  – выигрыш одного из партнеров. Примерами таких ситуаций служат отношения между продавцом и покупателем, адвокатом и прокурором, кредитором и дебитором, истцом и ответчиком и т.д.

Математические методы анализа конфликтных ситуаций объединяются под названием теории игр, сама конфликтная ситуация носит название игры, а стороны, участвующие в конфликте, называются игроками. Исход игры называется выигрышем (или проигрышем) игроков. Если в игре участвуют только два игрока, то игра называется парной. Если выигрыш одного игрока равен проигрышу другого, то игра называется антагонистической.

Для того чтобы решить игру, или найти решение игры, следует для каждого игрока выбрать стратегию, которая удовлетворяет условию оптимальности, т. е. один из игроков должен получать максимальный выигрыш, когда второй придерживается своей стратегии. В то же время второй игрок должен иметь минимальный проигрыш, если первый придерживается своей стратегии. Такие стратегии называются оптимальными. Оптимальные стратегии должны также удовлетворять условию устойчивости, т. е. любому из игроков должно быть невыгодно отказаться от своей стратегии в этой игре.

Игру можно представить в виде матрицы, в которой стро­ки – стратегии первого игрока (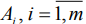), столбцы – стратегии второго игрока (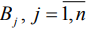), а элементы матрицы ( 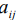– выигрыши первого игрока. Та­кую матрицу называют платежной.

Величина 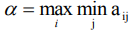 – гарантированный выигрыш, который может обеспечить себе первый игрок, – называется нижней ценой игры (максимином). Если второй игрок будет придерживаться своей минимакс­ной стратегии, то он гарантирован, что в любом случае про­играет не больше 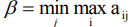, где β – верхняя цена игры (минимакс).

Для матричной игры справедливо неравенство .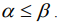

Если α = β, то такая игра называется игрой с седловой точ­кой, а пара оптимальных стратегий (А_iопт, B_jопт) – седловой точкой матрицы. В этом случае элемент a_ij = v называется ценой игры, является одновременно минимальным в i-й строке и j-м столбце. Если игра имеет седловую точку, то говорят, что она решается в чистых стратегиях.

Матричные игры в чистых стратегиях определенной размерности можно автоматизировать в табличном процессоре Microsoft Excel. При этом используются встроенные функции: МАКС, МИН, ЕСЛИ и ПОИСК РЕШЕНИЯ.

Если платежная матрица не имеет седловой точки, т.е. α < β, то поиск решения игры приводит к применению слож­ной стратегии, состоящей в случайном применении двух и более стратегий с определенными частотами. Такая сложная стратегия называется смешанной.

Решение задач по теории игр включает следующие этапы:

1) составление платёжной матрицы игры в соответствии с выбранными вариантами;

2) определение верхней и нижней цены игры;

3) если α ≠ β, то следует составить две взаимно-двойственные задачи;

4) решение задачи линейного программирования. Рекомендуется решать задачу на максимизацию целевой функции с ограничениями «меньше либо равно»;

5) формулирование выводов по задаче.

Рассмотрим решение  задачи теории игр в смешанных стратегиях с использованием надстройки «Поиск решения».

Торговая фирма разработала несколько вариантов плана продаж товаров на предстоящей ярмарке с учетом спроса покупателей. Получающиеся от их возможных сочетаний показатели дохода представлены в таблице.

Таблица 1

Bj Ai	B1	B2	B3		pi
A1	2	4	2	2	p1
A2	1	3	5	1	p2
A3	4	2	3	2	p3
	4	4	5	=2, =4
qj	q1	q2	q3

Определить оптимальную стратегию фирмы в продаже товаров на ярмарке, гарантирующую среднюю величину дохода при любом состоянии спроса, считая его неопределенным.

Задача сводится к игровой модели, в которой игра предприятия А против спроса В задана платёжной матрицей (табл.1).

Определим нижнюю и верхнюю цены игры в табл.1.

Так как α ≠ β, то седловая точка отсутствует, и оптимальное решение следует искать в смешанных стратегиях игроков: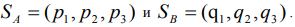

Составим две взаимно-двойственные задачи линейного программирования, обозначив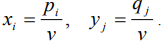 

Игрок А

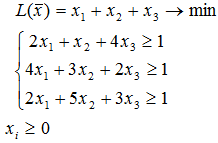
Игрок  B

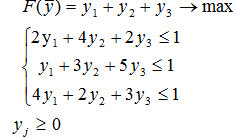
Решение двойственной задачи линейного программирования представлено на рис. 1-3.

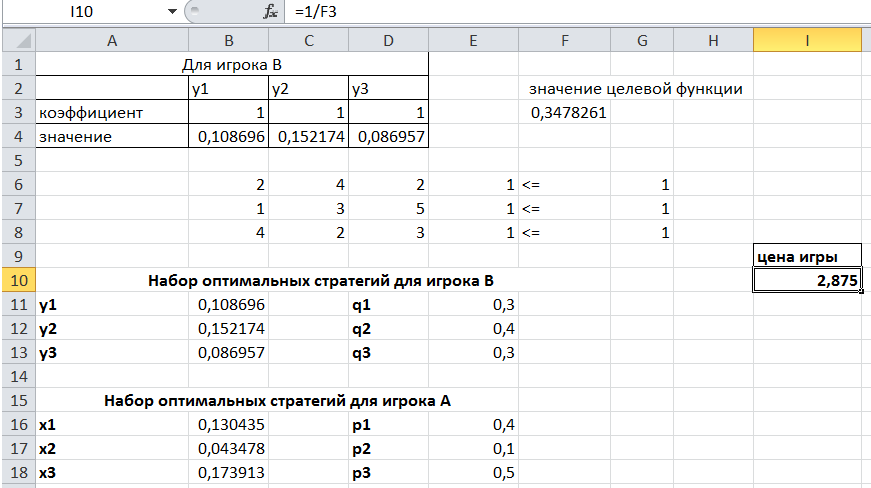
Рис.1. Решение задачи теории игр с помощью надстройки «Поиск решения»

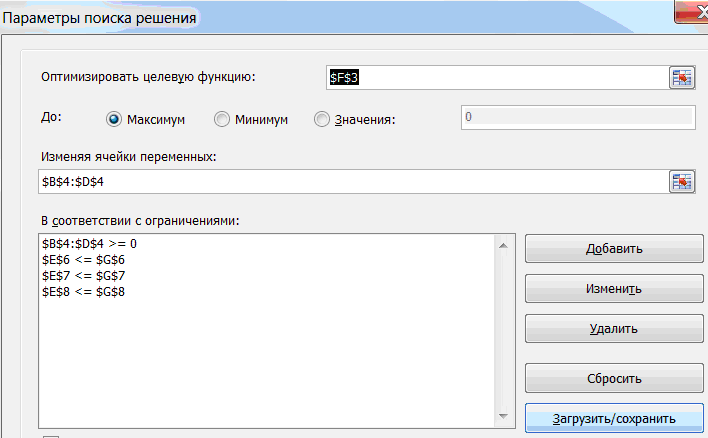
Рис.2. Параметры поиска решения

 При решении задачи линейного программирования с помощью надстройки «Поиск решения» решение двойственной задачи содержится в отчёте  Устойчивость: переменные для игрока В -  в столбце «Окончательное значение», а для игрока А - в столбце «Теневая цена».   

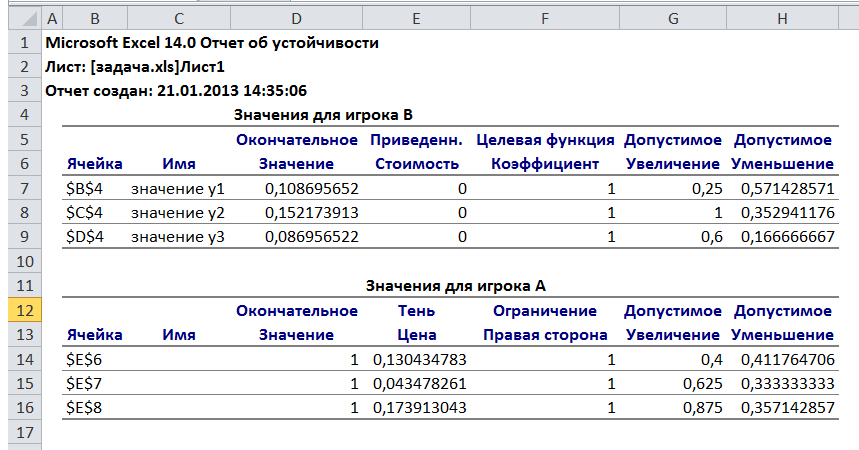
Рис.3. Отчет об устойчивости

Торговая фирма на ярмарке должна использовать план продаж А₁ с вероятностью 40%, А₂ с вероятностью 10%, А₃ с вероятностью 50%, при этом она получит доход не менее v = 2,875 ден. ед.

Основным преимуществом использования надстройки «Поиск решения», является то, что  упрощается сам процесс поиска решения и затрачивается намного меньше времени, чем, если бы вычисления производились вручную, это позволяет оптимизировать педагогический процесс.