DIFFERENTIAL ALGEBRAIC EQUATIONS OF CONTROL SYSTEM DYNAMICS

Шемелова О.В.

кандидат физико-математических наук, доцент кафедры математики

Нижнекамский химико-технологический институт (филиал) ФГБОУ ВПО «Казанский национальный исследовательский технологический университет»

Дифференциальные алгебраические уравнения динамики управляемых систем

Аннотация

В работе рассматривается задача построения уравнений динамики управляемых систем различной физической природы с голономными и неголономными связями. В работе уравнения динамики составляются в форме уравнений Лагранжа.

Ключевые слова: дифференциальные алгебраические уравнения.

Keywords: differential algebraic equations.

Физическая система, дифференциальные уравнения, динамика.

Задача управления динамикой систем различной физической природы может описываться уравнениями Лагранжа второго рода:

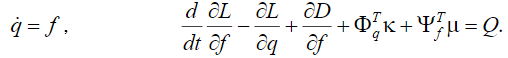
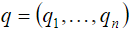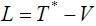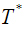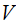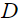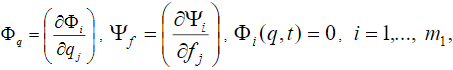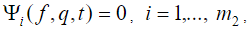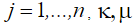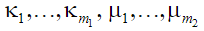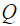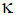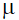Здесь  – обобщенные координаты,  – функция Лагранжа,  – кинетическая коэнергия,  – потенциальная энергия,  – диссипативная функция,   – уравнения голономных связей,  – уравнения неголономных связей,  – соответствующие векторы множителей Лагранжа,  – вектор обобщенных сил. Неопределенные множители   и  подбираются таким образом, чтобы уравнения связей, наложенных на обобщенные координаты и скорости системы, составляли её первые интегралы.

Уравнение Лагранжа второго рода преобразовывается к виду, разрешаемому относительно старших производных. Представление системы уравнений связей и уравнений Лагранжа второго рода в виде системы обыкновенных дифференциальных уравнений (ОДУ) первого порядка с известными частными интегралами позволяет использовать стандартные численные методы для решения уравнений движения [1]. В работе рассматривается задача построения уравнений динамики систем различной физической природы с голономными связями и неголономными связями.

Среди разнообразных явлений различной физической природы нередко можно встретить похожие явления, обнаруживающие одинаковые признаки и закономерности. В таких случаях говорят о физических аналогиях, или аналогичных системах. Физические аналогии, существующие между электрическими, механическими, акустическими и другими системами, давно с успехом используются при исследованиях и расчетах. Методы, основанные на применении аналогий, в ряде случаев 

оказываются весьма плодотворными при решении задач. Они позволяют сводить решения некоторых задач к решениям других (уже известных) задач (зачастую из другого раздела физики).

В работах [2, 3, 4, 5] предлагается обобщение и унификация множества переменных, которые описывают динамику физической системы. Некоторую классификацию возможно также провести среди величин, характеризующих динамическое поведение систем различной физической природы.

В [2, 5] определяется унифицированное множество переменных, которое включает следующие известные величины: усилие, расход импульс и перемещение. Данное унифицированное множество может быть использовано для получения уравнений динамики механической системы. В [1, 2, 4] показано, что использование динамических аналогий позволяет строить уравнения динамики для систем различной физической природы.

Соответствующие физические величины можно представить унифицированным множеством в виде таблицы 1.

Таблица 1.

Унифицированные множества переменных для физических систем

Система	Усилие  e	Расход  f	Перемещение  q	Импульс р
Механическая поступательная	Сила F	Скорость v	Положение  х	Количество движения p
Механическая вращательная	Вращающий момент t	Угловая скорость w	Угол  q	Момент количества движения Н
Электрическая	Электродвижущая сила е	Сила тока  i	Заряд  q	Магнитный поток l
Акустическая	Давление Р	Скорость течения материала Q	Объем  g	Давление импульса рр

Данная таблица позволяет сопоставить величины, аналогичные в каждой из четырех систем. Они указывают на динамическую аналогию, существующую между этими четырьмя системами.

Исследование всех систем различной физической природы может быть разделено на две части: на составление дифференциального уравнения, исходя из постановки задачи и физических законов, и на решение дифференциального уравнения.

Для построения уравнений динамики рассматриваются величины, которые характеризуют динамическое поведение систем различной физической природы. А так как уравнения динамики системы могут быть составлены в форме уравнений Лагранжа или в форме уравнений Гамильтона, среди динамических величин проводится некоторая классификация [5].

Уравнения динамики физической системы в форме Лагранжа получаются из общего уравнения динамики свободной системы [2, 6] в силу независимости обобщенных координат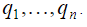 

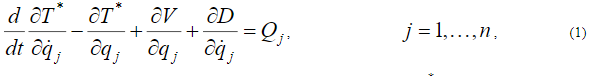
где 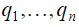 – координаты перемещений,  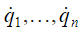– координаты расходов,  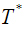– кинетическая коэнергия системы любой физической природы [5],  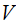– потенциальная энергия,  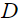– диссипативная функция,  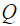– обобщенные силы.

Уравнение (1) соответствует системе 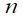 обыкновенных дифференциальных уравнений второго порядка с  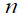неизвестными 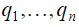. Основным условием вывода ОДУ Лагранжа (1) является независимость обобщенных координат системы. Допустим, что на координаты перемещения и расходы наложены ограничения, удовлетворяющие  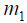голономным и  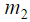неголономным связям:

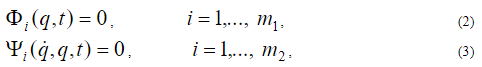
а также

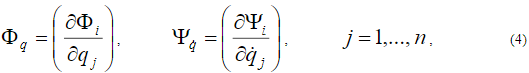
Для стабилизации связей (2), (3) вводятся уравнения программных связей [1]

Правые части 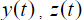 равенств (5), (6) определяются как решения дифференциальных уравнений

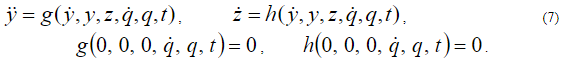
Уравнения (7) должны быть рассмотрены совместно с уравнениями динамики и начальными условиями

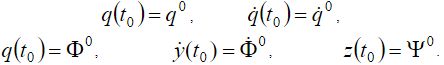
Равенства (5), (6) составляют уравнения программных связей. Уравнения (7) являются уравнениями возмущений связей [1]. Уравнения программных связей (5), (6), как и уравнения обычных связей, накладывают ограничения на обобщенные координаты перемещения и координаты расхода точек системы.

Тогда ОДУ Лагранжа, с учетом уравнений (5), (6), приводятся к виду

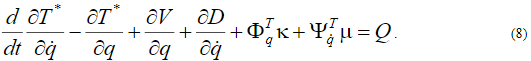
Движение, описываемое уравнением (8), должно удовлетворять также уравнениям программных связей (5) – (6). Таким образом, кинематические уравнения связей (5) – (6) добавляются к уравнениям движения (8) для получения векторов неизвестных множителе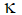й  и .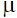

Система (5), (6), (8) представляет собой систему дифференциальных уравнений динамики Лагранжа, которая содержит в себе 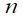неявных относительно 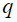ОДУ второго порядка,  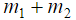уравнений связей ( 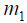голономных и  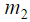неголономных связей).

Продифференцировав по времени слагаемое 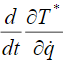, уравнение (8) можно представить в виде, допускающем решение относительно старших производных:

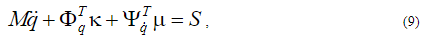
где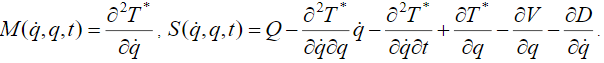 

Это уравнение вместе с алгебраическими уравнениями связей (5), (6) составляет ДАУ в форме Лагранжа. А, вводя вектор координат расхода 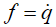 , множество ДАУ Лагранжа из  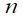ОДУ второго порядка преобразовывается к системе ОДУ первого порядка. Итак, система ДАУ имеет вид:

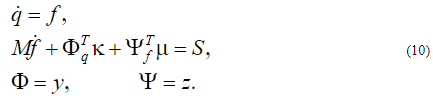
Выполнение соответствующих преобразований для уравнений (10), которое включает исключение множителе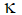й  и 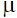, а также построение уравнений возмущений связей для учета стабилизации связей, позволяет получить следующую систему  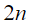уравнений первого порядка:

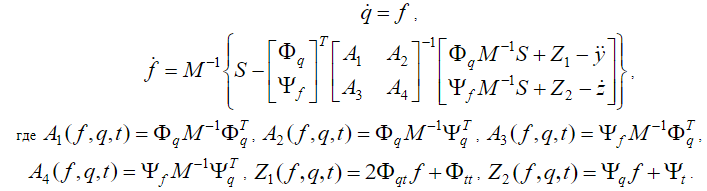
Представление системы уравнений связей и уравнений Лагранжа второго рода в виде системы ОДУ первого порядка с известными частными интегралами позволяет использовать стандартные численные методы для решения уравнений динамики.