NONPARAMETRIC ADAPTIVE CONTROL OF PROCESS SEQUENCE

Корнет М.Е.¹, Раскин А.В.², Раскина А.В.³

¹ORCID: 0000-0003-4100-5644, Аспирант, Сибирский государственный аэрокосмический университет имени академика М.Ф. Решетнева, ²ORCID: 0000-0002-3263-0571, Магистр, Сибирский государственный аэрокосмический университет имени академика М.Ф. Решетнева, ³ORCID: 0000-0002-8161-8317, Аспирант, Сибирский федеральный университет

НЕПАРАМЕТРИЧЕСКОЕ АДАПТИВНОЕ УПРАВЛЕНИЕ ПОСЛЕДОВАТЕЛЬНОСТЬЮ ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ

Аннотация

Рассматривается задача управления цепочкой технологических объектов в условиях непараметрической неопределенности. Среди последовательно соединенных элементов могут выступать различные типы объектов, к которым относятся динамические либо статические объекты с запаздыванием.  В данном случае параметрические структуры моделей с точностью до параметров остаются неизвестными. Такая ситуация часто возникает в случае малоизученных объектов, обоснованно подобрать параметрическую структуру для которых не представляется возможным. В статье рассматривается ситуация, когда у каждого локального объекта уже имеется свой контур управления, включающий типовое устройство регулирования (П,ПИ,ПИД регуляторы). Предлагается добавить внешний контур управления, который будет корректировать задающие воздействия локальных контуров. В статье приводятся непараметрические алгоритмы управления для внешнего контура.

Ключевые слова: адаптивное управление, непараметрическая теория, последовательность технологических объектов, динамический объект, безынерционный объект с запаздыванием.

Kornet M.E.¹, Raskin A.V.²,  Raskina A.V.³

¹ORCID: 0000-0003-4100-5644, Postgraduate student, Reshetnev Siberian State Aerospace University, ²ORCID: 0000-0002-3263-0571, Master of Science, Reshetnev Siberian State Aerospace University, ³ORCID: 0000-0002-8161-8317, Postgraduate student, Siberian Federal University

NONPARAMETRIC ADAPTIVE CONTROL OF PROCESS SEQUENCE

Abstract

The article considers the task of managing a chain of technological facilities in a non-parametric uncertainty. Among the successively connected elements there might be different types of objects that are either dynamic or static objects with delay. In this case, the structure of parametric models is unknown. This situation often arises in the case of poorly known objects, it is reasonable to choose a parametric structure for which it is impossible. The article deals with the situation where each local object already has its own control loop, including a model control device (P, PI, PID controllers). It is proposed to add an external control circuit, which will adjust the set point local loops. The article presents non-parametric control algorithms for the outer loop.

Keywords: adaptive control, nonparametric theory, the sequence of technological objects, dynamic object, the instantaneous object with delay.

Задача управления сложными многомерными процессами, технологическая цепочка которых может представлять собой различные схемы производства, такие как параллельные, последовательные, или их комбинации безусловно на сегодняшний момент является актуальной для многих отраслей промышленности. В данном случае схема управления будет содержать уже не один локальный объект, а группу объектов, соединённых между собой. Следует учитывать, что при управлении цепочкой технологических объектов алгоритм регулирования общей последовательностью должен строиться таким образом, чтобы алгоритмы управления локальными объектами были согласованны между собой. На сегодняшний день разработаны многочисленные алгоритмы адаптивного управления параметрического типа [1,2]. Основной их особенностью является знание о параметрической структуре модели объекта с точностью до параметров на основании априорной информации или предварительных исследований. В условиях недостатка априорной информации одним из путей решения данной задачи является введение в схему управления непараметрического внешнего контура, который будет формировать задающие воздействия для каждого локального регулятора. Это позволит более качество управлять всей последовательностью. В статье приводятся адаптивные непараметрические алгоритмов определения задающих воздействий для внешнего контура управления.

Постановка задачи. Для дальнейшего нам необходим анализ следующей блок-схемы (рис.1).

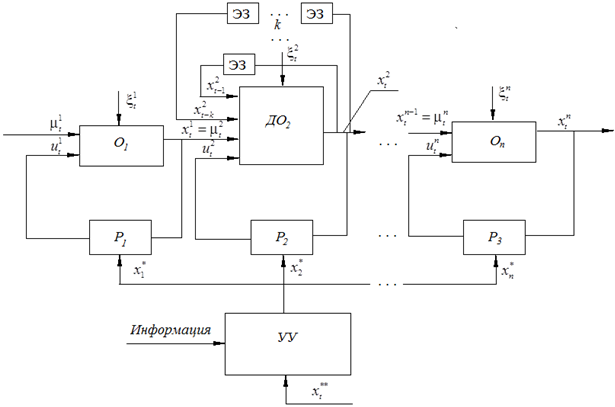
Рис. 1 – Схема двухконтурного управления последовательностью технологических процессов

На рисунке 1 приняты обозначения: 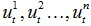 - входные управляемые воздействия,  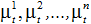-входные контролируемые, но не управляемые воздействия,  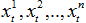- выходные воздействия, О₁,…, О_n – локальные безынерционные объекты с запаздыванием, ДО₂ – динамический объект,  ЭЗ - элемент запаздывания,  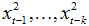- выходные воздействия динамического объекта, запаздывающие на соответствующее число шагов, Р₁, Р₂, Р₃ – типовые регуляторы (П,ПИ,ПИД),  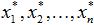- задающие воздействия для локальных типовых регуляторов, УУ – устройства управления (внешний контур), Информация – все доступные измерения входных-выходных переменных локальных процессов  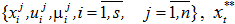- задающее воздействие для внешнего контура управления,  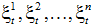 - внешние помехи, действующие на локальные процессы. На рисунке 1 показано, что среди локальных объектов технологической цепочки могут встречаться как динамические объекты, так и безынерционные объекты с запаздыванием. В общем случае все описанные переменные представляют собой векторы. Для простоты рассмотрим скалярный случай. Безынерционный объект с запаздыванием может быть представлен в следующем виде:

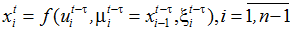  (1)

где f(^.) – неизвестный функционал, τ – запаздывание, которое по разным каналам связи может отличаться, но из соображений простоты в тексте мы приняли единое обозначение запаздывания τ. Следует заметить, что выходная переменная объекта, которая воздействует на следующий объект, по существу является неуправляемой входной переменной.

В случае динамического объекта, состояние системы в данный момент времени t зависит как от входных воздействий, так и от ее состояний в прошлом 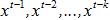. Другими словами, динамическая система может быть описана следующим уравнением:

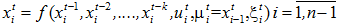   (2)

где x_t – выходная переменная процесса, u_t - управляющее воздействие, k – «глубина» памяти динамического объекта (в терминологии А. А. Фельдбаума)  [3]. Если проводить аналогию с описанием исследуемого процесса в непрерывном времени в виде дифференциальных уравнений, то k – порядок старшей производной в соответствующем уравнении. В обоих случаях существенным является то, что вид функционала f(^.) не определен с точностью до параметров.

Задача управления сводится к разработке адаптивных непараметрических алгоритмов управления для внешнего контура. Предлагаемое устройство управления будет формировать задающие воздействия для локальных типовых регуляторов, таким образом, чтобы итоговые управляющие воздействия для локальных объектов были согласованы между собой.

Для всякого технологического процесса на производстве установлен технологический регламент, который определяет, в каком диапазоне значений должна находиться величина той или иной переменной процесса. Для многих производств характерен довольно широкий диапазон изменения значений технологических переменных [4-5]. Рассмотрим следующую схему (рис. 2).

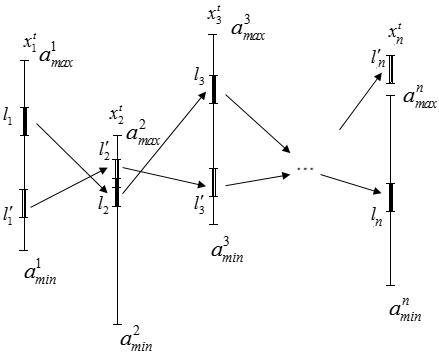
Рис. 2 – Схема ведения процесса в рамках технологического регламента

На рис. 2 приняты обозначения: 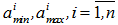  – минимальная и максимальная границы диапазона  допустимых значений переменных, определяемые технологическим регламентом;  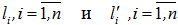- интервалы в рамках технологического регламента, показывающие различные варианты ведения процесса на i – тых итерациях;  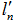– требуемая область значения итоговой выходной переменной  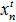всего технологического процесса, определяющая качество готового продукта.

На рисунке 2 изображены два варианта ведения технологического процесса 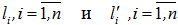 . В обоих случаях на всех промежуточных итерациях  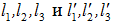и  процесс ведется в рамках диапазона 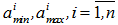, то есть иными словами в рамках технологического регламента: 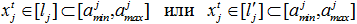. Но, в то же время, ведение технологического процесса по траектории  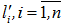 не приводит к попаданию итоговой выходной переменной  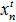в требуемую область значений. Таким образом, можно сделать вывод, что для рационального ведения процесса представляется целесообразным осуществлять технологический процесс в соответствии со следующей схемой. Сначала нужно определить интервал  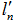– требуемую область значений переменной 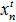, далее формировать управляющее воздействие  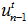для локального объекта  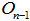таким образом, чтобы гарантированно обеспечить попадание в область 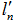. То же самое провести для оставшихся объектов 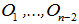. Таким образом управляющее устройство должно формировать задающие воздействия  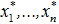для локальных регуляторов начиная с конца цепочки и двигаясь в обратном направлении, каждый раз учитывая вычисленные на предыдущих шагах воздействия .

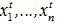Непараметрический алгоритм управления. В качестве задающего воздействия для регулятора локального безынерционного объекта O_j с запаздыванием может быть принята следующая непараметрическая оценка функции регрессии (Надарая-Ватсона [6]) по наблюдениям 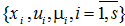  в дискретном виде 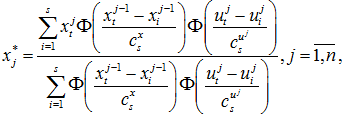[3]:

  (3)

где 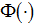 – ядерная колоколообразная функция,  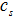– коэффициент размытости ядра, соответствующий каждой переменной объекта, s – объем выборки наблюдений. Ядерная функция и коэффициент размытости ядра удовлетворяют некоторым условиям сходимости [6].

В случае динамического объекта задающее воздействие имеет вид:

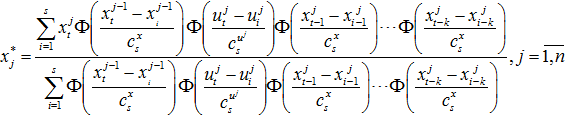  (4)

Параметр размытости 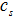 определяется путем решения задачи минимизации квадратичного показателя соответствия выхода объекта и задающего воздействия, основанного на «методе скользящего экзамена»

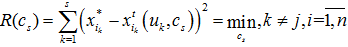  (5)

когда в уравнениях (3-4) исключается j-я переменная, предъявляемая для экзамена.

Заключение. Таким образом в статье рассмотрена задача управления группой объектов в варианте последовательно распределённых элементов последовательности. Приведены непараметрические алгоритмы адаптивного управления. В этом случае использование типовых алгоритмов регулирования без внешнего контура управления может привести к значительным ошибкам при регулировании. В итоге, при управлении последовательностью процессов сначала необходимо определить соответствующие задающие воздействия для выходных переменных, а уже затем применять типовые алгоритмы регулирования. Это является существенной особенностью построения управляющей системы в отличии от традиционных алгоритмов управления.

 

Список литературы / References

1. Цыпкин Я. З. Адаптация и обучение в автоматических системах. / Я.З. Цыпкин – М.: Наука, 1968. – 400 с.
2. Эйкхофф П. Основы идентификации систем управления. / П. Эйкхофф – М.: Мир, 1975. – 681 с.
3. Фельдбаум А. А. Основы теории оптимальных автоматических систем / А.А. Фельдбаум – М.: Физматгиз, 1963. – 552 с.
4. Медведев А. В. Основы теории адаптивных систем / А.В. Медведев – Краснорск: изд. СибГАУ, 2015. – 525 с.
5. Корнеева А.А. Об адаптивном управлении последовательностью технологических объектов /А.А. Корнеева, М.Е. Корнет, Н А. Сергеева, Е. А. Чжан. // Вестник СибГАУ. – 2015. – Т. 16. - № 1. – С. 72–78
6. Надарая Э. А. Непараметрическое оценивание плотности вероятностей и кривой регрессии / Э.А. Надарая – Тбилиси: Изд-во Тбилис. ун-та., 1983. – 194 с.

Список литературы на английском языке / References in English

1. Tsypkin Ja. Z. Adaptatsiya i obuchenie v avtomaticheskikh sistemakh [Adaptation and learning in automatic systems] / Ja. Z. Tsypkin. – Moscow: Nauka Publ., 1968. - 400 p. [in Russian]
2. Eykhoff P. Osnovy identifikatsii sistem upravleniya [Identity-based control systems] / P. Eykhoff. – Moscow: Mir Publ., 1975. - 681 p. [in Russian]
3. Fel'dbaum A. A. Osnovi teorii optimal’nikh avtomaticheskih sistem [Fundamentals of the theory of optimal automatic systems] / A. A. Fel'dbaum. – Moscow: Fizmatgiz Publ., 1963. - 552 p. [in Russian]
4. Medvedev A. V. Osnovi teorii adaptivnih sistem [Basic theory of adaptive systems] / A. V. Medvedev. – Krasnoyarsk: SibSAU Publ., 2015. - 525 p. [in Russian]
5. 5. Korneeva А. А. Ob adaptivnom upravlenii posledovatel'nost'ju tehnologicheskih obektov [On the sequence of adaptive management of technological objects On the sequence of adaptive management of technological objects] / А. А. Korneeva, М.Е. Kornet, Н А. Sergeeva, Е. А. Chzhan // Vestnik SibGAU [Bulletin of the SibCAU]. - 2015. - Т.16. - № 1. - p. 72–78. [in Russian]
6. Nadaraya E. A. Neparametricheskie otsenki plotnosti veroyatnosti i krivoy regressii [Non-parametric estimation of the probability density and the regression curve] / E. A. Nadaraya. – Tbilisi: izd. Tbil. un-tа Publ., 1983. - 194 p. [in Russian]