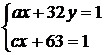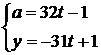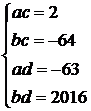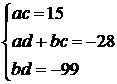ABOUT IMPROVEMENT OF PROFESSIONAL TRAINING OF FUTURE TEACHER OF MATHEMATICS

Хамов Г.Г.¹, Тимофеева Л.Н.²

¹ Доктор педагогических наук, Российский государственный педагогический университет им. А.И. Герцена, ² Кандидат педагогических наук, Военно-космическая академия им. А.Ф. Можайского

О СОВЕРШЕНСТВОВАНИИ ПРОФЕССИОНАЛЬНОЙ ПОДГОТОВКИ БУДУЩЕГО УЧИТЕЛЯ МАТЕМАТИКИ

Аннотация

В работе рассматривается один из путей совершенствования профессиональной подготовки будущего учителя математики посредством заданий на составление задач теоретико-числового содержания, что обеспечивает вовлечение студентов в исследовательскую деятельность и способствует повышению интереса к обучению.

Ключевые слова: делимость целых чисел, деление с остатком, теоретико-числовые задачи, неопределенные уравнения.

 

Khamov G.G.¹, Timofeeva L.N.²

¹ PhD in Pedagogy, Herzen State Pedagogical University of Russia, ² PhD in Pedagogy, Mozhaisky Military Space Academy

ABOUT IMPROVEMENT OF PROFESSIONAL TRAINING OF FUTURE TEACHER OF MATHEMATICS

Abstract

This paper examines one of the ways of improving professional preparation of future teachers of mathematics through job preparing the problems for number-theoretic content, which ensures the involvement of students in research activities and promotes interest in learning.

Keywords: divisibility of integers, division with remainder, number-theoretic tasks, uncertain equation.

В соответствии с федеральным государственным образовательным стандартом высшего профессионального образования организация процесса обучения в высшей школе направлена на создание условий для непрерывного формирования профессиональной компетентности будущего специалиста. В связи с этим, в процессе математической подготовки будущего учителя необходимо формировать содержание, методы и средства обучения, способствующие: активизации самостоятельной познавательной деятельности студентов; овладению методами познания; повышению уровня методической компетентности; творческому использованию полученных знаний [1] – [3].

Одним из путей формирования профессиональной компетентности будущего учителя математики могут быть задания на конструирование студентами собственных задач. Покажем на примере теоретико-числового материала возможности использования такого типа заданий в учебном процессе, при этом участие студентов в составлении задач позволит постепенно приучать их к самостоятельной математической деятельности, развивать способности, пробуждать желание учиться.

Одним из приемов составления задач – обобщение условия известной задачи на более общий случай или составление аналогичной задачи с другими данными. Например, задача: «может ли сумма квадратов девяти последовательных натуральных чисел быть квадратом натурального числа?» обобщается на случай любой натуральной степени : «может ли сумма квадратов девяти последовательных натуральных чисел быть -й степенью натурального числа?». Действительно, так как сумма квадратов девяти последовательных натуральных чисел приводится к выражению, которое делится на число 3, но не делится на 9, то она не может делиться и на любую натуральную степень 3, кроме первой.

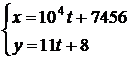В условии задачи [4] «на какое наименьшее натуральное число надо умножить число 7, чтобы произведение оканчивалось числом 123?» могут быть изменены числовые данные. Например, «на какое наименьшее натуральное число надо умножить число 11, чтобы произведение оканчивалось числом 2016?». Обозначив искомое число , получим уравнение , множество решений которого определяется по формулам ,  – целое число.

Наименьшее натуральное число  получаем при : , .

Можно исследовать со студентами разрешимость уравнения  в натуральных числах  методом остатков. В данном случае определяем возможные остатки от деления левой и правой частей на число 3 и убеждаемся, что левая часть уравнения может давать остатки , а правая . Поэтому уравнение в натуральных числах  решений не имеет. Далее предлагаем студентам обобщить задачу, при этом в качестве оснований степеней вместо конкретных чисел ввести обобщенные формулы, используя теорему о делении с остатком. В результате получим уравнение:

,

где  – целые неотрицательные числа, которое в натуральных числах  неразрешимо.

Другое задание может быть сформулировано таким образом: определите возможные остатки от деления суммы квадратов трех целых чисел  на число 8, суммы кубов  на число 9 и составьте неразрешимые в целых числах уравнения, содержащие эти выражения и число 2016.

Так как сумма квадратов  при делении на 8 не дает остаток 7, а сумма кубов  при делении на 9 не дает остатков 4 и 5, то возможными вариантами ответа могут быть:

.

Рассмотрим далее некоторые методы составления теоретико-числовых задач в форме неопределенных уравнений. Опишем процесс составления неопределенных уравнений с использованием некоторых известных формул разложения многочлена на множители, при этом наиболее интересный вариант получается в случае, когда составленное уравнение будет разрешимо в целых числах.

Формулу   (1)

применим к составлению уравнения вида

. (2)

Подбираем один из коэффициентов и свободный член уравнения (2), например, ,  (для минимизации вычислений при составлении уравнения и при его решении, свободный член  берем равным 1 или простому числу).

С помощью формулы (1) составляем систему:

 (3)

(или другой возможный вариант системы с отрицательными правыми частями).

Из второго уравнения системы (3) имеем , полагаем, например, , тогда . Первое уравнение системы примет вид  , решения которого находятся по формулам:

,  – целое число.

Возьмем, допустим, , тогда , . Получаем уравнение

  ,  ,(4)

с одним целочисленным решением x = 31, y = 1, в чем убеждаемся, проверив другой возможный вариант системы 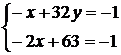, которая не имеет целых решений.

Сконструированное уравнение можно усложнить, заменив переменную , любой другой натуральной степенью , и получим уравнение, которое имеет одно целочисленное решение  при  – нечетном и два решения  и  при  – четном:

  .

При решении такого вида уравнений затруднения вызывает разложение левой части уравнения на множители. Для решения этой задачи надо воспользоваться формулой (1), с помощью которой получаем систему:

  (5)

Из равенства  следует, что  – нечетные числа, поэтому из первого равенства системы (5) следует, что  (или ),  (или ). Поэтому  (или ) и из последнего равенства системы (5):  (или ). И в том и другом случае получим разложение уравнения (4).

Опишем процесс составления разрешимого в целых числах неопределенного уравнения вида    (6)

применением формулы .    (7)

Вначале выбираем один из коэффициентов при квадратах переменных, например, , то есть , . В соответствии с формулой (7) составляем систему 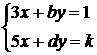.                                                                (8)

В первом уравнении подбираем либо число , либо значение для переменной . Полагаем, например, , получаем уравнение , множество решений которого находится по формулам:

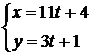,  – целое число.

Наиболее простейший выбор: , , . Тогда второе уравнение системы (8) принимает вид , множество решений которого: 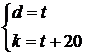,  – целое число.

Наименьшая вычислительная работа при нахождении всех решений составляемого уравнения будет в случае, если число  простое, выбираем, например, , , . Искомое уравнение

  , (9)

множество решений: .

Заметим, что если в составленном уравнении переменную  заменить нечетной степенью, например, , то получим уравнение

,

имеющее те же два решения.

При решении уравнения (9) используем формулу (7) и получаем систему

  (10)

Выбирая один из возможных вариантов чисел  из первого уравнения системы (10) (или  из последнего) получаем систему двух уравнений с двумя переменными  (или ), решение которой приводит к квадратному уравнению, целые решения которого будут искомыми числами.

Пример уравнения (6) с заданным числом .

  .

Множество решений: .

Использование в учебном процессе заданий на конструирование студентами задач предоставляет широкие возможности как на учебных занятиях, так и для самостоятельной работы, например, при выполнении индивидуальных заданий, курсовых проектов. Обучение студентов составлению задач способствует повышению уровня их профессиональной компетентности. Рассмотренные в работе примеры задач арифметического содержания посвящены вопросам, которые включены в программы классов с углубленным изучением математики. Такого содержания задачи нередко включаются в задания математических олимпиад.

Литература

1. Тестов В.А. Математическое образование в условиях сетевого пространства. //Образование и наука, №2, 2013. – С.111-121.
2. Тестов В.А. Основные проблемы развития математического образования. //Образование и наука, №4, 2014. – С. 3-16.
3. Тихомиров А.С, Кузнецова И.В., Кытманов А.А., Тихомиров С.А., Трошина Т.Л. Формирование методической компетентности будущего учителя математики на основе фундирования опыта студентов в сетевом сообществе.// Ярославский вестник. Психолого-педагогические науки = Yaroslave pedagogical bulletin. Научный журнал. – Ярославль: Изд-во ЯГПУ, 2014. – №3. – Том 2 (Психолого-педагогические науки). – С. 68-72.
4. Хамов Г.Г. Элементы теории диофантовых уравнений в задачах и упражнениях: Учебное пособие. Л.: Изд-во ЛГПИ им. А.И.Герцена, 1986. 73 с.

References

1. Testov V.A. Matematicheskoe obrazovanie v uslovijah setevogo prostranstva. //Obrazovanie i nauka, №2, 2013. – S.111-121.
2. Testov V.A. Osnovnye problemy razvitija matematicheskogo obrazovanija. //Obrazovanie i nauka, №4, 2014. – S. 3-16.
3. Tihomirov A.S, Kuznecova I.V., Kytmanov A.A., Tihomirov S.A., Troshina T.L. Formirovanie metodicheskoj kompetentnosti budushhego uchitelja matematiki na osnove fundirovanija opyta studentov v setevom soobshhestve.// Jaroslavskij vestnik. Psihologo-pedagogicheskie nauki = Yaroslave pedagogical bulletin. Nauchnyj zhurnal. – Jaroslavl': Izd-vo JaGPU, 2014. – №3. – Tom 2 (Psihologo-pedagogicheskie nauki). – S. 68-72.
4. Hamov G.G. Jelementy teorii diofantovyh uravnenij v zadachah i uprazhnenijah: Uchebnoe posobie. L.: Izd-vo LGPI im. A.I.Gercena, 1986. 73 s.