THE DESIGN OF PROBABILISTIC ALGORITHM OF OPTIMAL CHOICE OF VARIANTS OF ADOPTION DECISION SYSTEMS
Ильницкий А.В.1, Сумин В.И.2
1Соискатель, Воронежский государственный педагогический университет; 2Доктор технических наук, профессор кафедры управления и информационно-технического обеспечения, Воронежский институт ФСИН России
РАЗРАБОТКА ВЕРОЯТНОСТНОГО АЛГОРИТМА ОПТИМАЛЬНОГО ВЫБОРА ВАРИАНТОВ СИСТЕМ ПРИНЯТИЯ РЕШЕНИЙ
Аннотация
В статье рассмотрена проблема разработки вероятностного алгоритма оптимального выбора вариантов систем принятия решения.
Ключевые слова: метод оптимизации, итерационная процедура.
Ilnitskiy A.V.1, Sumin V.I.2
1Applicant, Voronezh State Pedagogical University; 2Doctor of technical sciences, professor of chair management and information-technical maintenance, Voronezh institute of the Russian Federal Penitentionary Service
THE DESIGN OF PROBABILISTIC ALGORITHM OF OPTIMAL CHOICE OF VARIANTS OF ADOPTION DECISION SYSTEMS
Abstract
The given article describes the problem of the design of probabilistic algorithm of optimal choice of variants of adoption decision systems.
Keywords: optimization's method, iteration procedure.
Решение задач оптимизации осуществляется как правило методами векторной оптимизации, в виде многоальтернативной оптимизации.
Общая оптимизационная модель представлена ниже:
![]()
Где I1- множество требований критериев оптимизации; I2 - множество требований к ограничению системы.
Использование метода многоальтернативной оптимизации предполагает использование в качестве инвариантной части вероятностного алгоритма дискретной оптимизации псевдобулевой функции векторного аргумента, к которому предъявляется требование булевости.
Следовательно, необходимо перевести переменные, которые описываются в матричном виде в векторный вид:
![]()
Решения рассматриваемой задачи оптимизации осуществляется на основе гибкой схема направленного перебора и формируется на основе обучения свойствам целевой функции с использованием текущей информации о ее значении.
Итерационная процедура настройки координат вектора в характеристиках математического ожидания позволяет выбрать в качестве схемы перебора случайный механизм в виде:
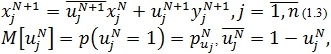
где ![]() - случайная булева величина,
- случайная булева величина,
![]() - случайная булева величина,
- случайная булева величина,
![]() - номер итерации.
- номер итерации.
В итерационной процедуре (1.3) для повышения ее вычисления определяют последовательное выделение отдельной координаты, что позволяет этот процесс описать следующим движением во множестве случайных векторов:
![]()
где: W - случайная булева величина: p(W = 1) = р, ![]()
W – является параметром, который позволяет управлять процессом ветвления.
Допустимое множество вариантов решений можно проиллюстрировать в виде дерева, рис. 3.2.
Для ![]() = 1 возможен спуск по дереву вариантов (х1,х2,...,хк) - частичный вариант).
= 1 возможен спуск по дереву вариантов (х1,х2,...,хк) - частичный вариант).
Для ![]() = 0 происходит возврат в начальную вершину дерева вариантов.
= 0 происходит возврат в начальную вершину дерева вариантов.
Для вектора ![]() варьирование осуществляется на основе экспертных данных.
варьирование осуществляется на основе экспертных данных.
Движением во множестве случайных векторов согласно (1.4) для некоторых вероятностных характеристик осуществляется согласно (1.5).
Движение (1.4) может быть выполнено либо в реализациях, либо в некоторых вероятностных характеристиках. В последнем случае
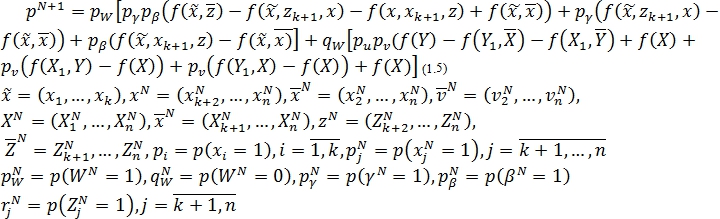
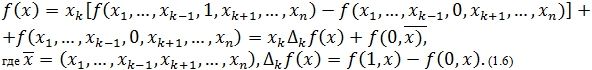
Параметры движения (W, V, U, Z, X (1.5)) определяются за счет выполнения условия локального улучшения (УЛУ) вариационного типа ![]() и (1.6) принимает вид:
и (1.6) принимает вид:
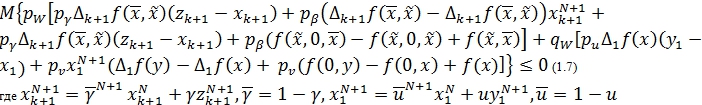
Выполнение УЛУ (1.7) осуществимо по трем направлениям:
- не производится осреднение, и неравенство выполняется для каждого вектора yN+1 , xN и алгоритмы используют только случайные вектора;
- осреднение осуществляется по всем переменным, неравенства и алгоритмы используют только случайные вектора, предусматривающие изменение параметров генераторов случайных величин;
- осреднение осуществляется по части переменных, неравенства и алгоритмы используют только случайные вектора, предусматривающие изменение вероятностных характеристик в зависимости от реализаций известных случайных величин.
Следовательно УЛУ необходимо производить на основе реализации случайных векторов.
Литература
- Березовский Б.А., Гнедин А.В. Задача наилучшего выбора. М.: Наука, 1984. 196 с.
- Грешилов А.А. Как принять наилучшее решение в реальных условиях. М: Радио и связь, 1991. 320 с.
- Кини П.Дж., Райфа X. Принятие решений при многих критериях: предпочтения и замещения. М.: Радио и связь, 1981. 560 с.
- Ларичев О.И., Мошкович Е.М. Качественные методы принятия решений. Вербальный анализ решений. М.: Наука, 1996. 208 с.
