METHODS OF MODELING EQUATION OF STATE METEOROLOGICAL SYSTEM BASED ON NEURAL NETWORKS
Матвеев М.Г.1, Михайлов В.В.2, Сирота Е.А.3, Новицкий Г.С.4
1доктор технических наук, профессор, заведующий кафедрой информационных технологий управлений факультета компьютерных наук, Воронежский государственный университет; 2доктор технических наук, начальник метеорологического факультета ВУНЦ ВВС "Военно-воздушная академия имени профессора Н.Е. Жуковского и Ю.А. Гагарина"; 3кандидат физико-математических наук, доцент кафедры цифровых технологий факультета компьютерных наук, Воронежский государственный университет; 4 Аспирант, Воронежский государственный университет
МЕТОДИКА МОДЕЛИРОВАНИЯ УРАВНЕНИЯ СОСТОЯНИЯ МЕТЕОРОЛОГИЧЕСКОЙ СИСТЕМЫ НА БАЗЕ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
Аннотация
Целью данной работы явилось построение системы векторной авторегрессии для анализа динамики нестационарного векторного метеорологического процесса, а также экспериментальное обоснование возможности использования моделей векторной авторегрессии с переменными параметрами для анализа динамики нестационарных процессов в метеорологии с помощью искусственных нейронных сетей.
Ключевые слова: векторная авторегрессия, нестационарный метеорологический процесс, уравнения состояний, искусственная нейронная сеть.
Matveev M.G.1, Mihailov V.V.2, Sirota E.A.3, Novickiy G.S.4
1PhD in technical science, professor, Voronezh State University; 2PhD in technical science, professor, VVS Academy named after Gagarin and Jukovsky; 3PhD in Physics and mathematics, assosiate professor, Voronezh State University; 4Postgraduate student, Voronezh State University;
METHODS OF MODELING EQUATION OF STATE METEOROLOGICAL SYSTEM BASED ON NEURAL NETWORKS
Abstract
The aim of this work was to construct a system of vector autoregression to analyze the dynamics of unsteady vector meteorological process, as well as the possibility of using experimental basis vector autoregression models with variable parameters for the analysis of the dynamics of non-stationary processes in meteorology using neural networks.
Keywords: vector autoregression, non-stationary meteorological processes, equation of state, neural network.
Модели типа «вход-выход» обеспечивают требуемый уровень адекватности, лишь при фиксированном состоянии моделируемой системы, т.е. при некоторых однородных условиях протекания моделируемых процессов и явлений. Изменения однородности условий могут находить отражение в зависимости параметров модели «вход-выход» от входных переменных и, как правило, эта зависимость стохастическая и не известна. Примером такой ситуации является известная модель векторной авторегрессии [1], которая при использовании в метеорологии для анализа изменения во времени t температурных полей x имеет вид [2]
![]() (1)
(1)
Рассмотрим модель (1) более подробно. Анализ динамических процессов изменения атмосферной температуры предполагает рассмотрение скалярных полей температуры в трехмерном пространстве земной атмосферы. Дискретное представление этого пространства - трехмерная сетка с постоянными шагами по меридианам, параллелям и расстоянию от поверхности земли. Изменение температуры в узлах сетки рассматривается как случайный процесс, порождающий временной ряд температур. Динамика температуры в каждом узле сетки с конкретными пространственными координатами зачастую определяется не столько местными факторами погоды, сколько влиянием конвективной составляющей, которая может оцениваться изменением аналогичных переменных в смежных узлах. Следствием этого является взаимная коррелированность временных рядов температур в узлах и необходимость моделирования многомерного временного ряда [3].
Целью данной работы явилось построение системы векторной авторегрессии для анализа динамики нестационарного векторного метеорологического процесса, а также экспериментальное обоснование возможности использования моделей векторной авторегрессии с переменными параметрами для анализа динамики нестационарных процессов в метеорологии с помощью искусственных нейронных сетей.
Вид модели (1) в более подробной интерпретации определим как векторную авторегрессию следующего вида:
![]() (2)
(2)
где ![]() - вектор значений температуры в n смежных узлах сетки;
- вектор значений температуры в n смежных узлах сетки;![]() - матрица параметров модели,
- матрица параметров модели, ![]() - временной лаг авторегрессии;
- временной лаг авторегрессии; ![]() - вектор серийно некоррелированных ошибок, о которых предполагается, что они имеют нулевое среднее и интерпретируются как белый шум. Если векторный процесс
- вектор серийно некоррелированных ошибок, о которых предполагается, что они имеют нулевое среднее и интерпретируются как белый шум. Если векторный процесс ![]() - стационарный и эргодический, то параметры
- стационарный и эргодический, то параметры ![]() векторной авторегрессии (2) находятся как МНК-оценки по однородным (полученным при одинаковых условиях) статистическим данным. В этом случае параметры представляют собой константы, не изменяющиеся во времени.
векторной авторегрессии (2) находятся как МНК-оценки по однородным (полученным при одинаковых условиях) статистическим данным. В этом случае параметры представляют собой константы, не изменяющиеся во времени.
В большинстве практических приложений, в метеорологии в частности, однородность данных обеспечивается лишь на сравнительно непродолжительных временных отрезках формирования временного ряда, более того границы этих отрезков, как правило, невозможно четко определить. Формально такое положение можно рассматривать как непрерывную зависимость параметров модели (2) от времени ![]() - и, следовательно, необходимость их корректировки по мере изменения условий. Изменение параметров
- и, следовательно, необходимость их корректировки по мере изменения условий. Изменение параметров ![]() может обуславливать нестационарность векторного процесса.
может обуславливать нестационарность векторного процесса.
В данной работе предлагается рассматривать векторную авторегрессию (2) как модель типа «вход-выход» с измеряемыми входными переменными ![]() и выходными переменными
и выходными переменными ![]() , а ее параметры
, а ее параметры ![]() как совокупность внутренних характеристик процесса, определяющих его состояние (условия функционирования) в данный момент времени. Пространство состояний случайного процесса может быть задано системой уравнений состояния
как совокупность внутренних характеристик процесса, определяющих его состояние (условия функционирования) в данный момент времени. Пространство состояний случайного процесса может быть задано системой уравнений состояния
![]() (3)
(3)
Для построения уравнений состояния ![]() необходимо определить признаки, по которым можно было бы оценивать стационарность условий протекания процесса или другими словами, однородность статистических данных. Если удается выделить классы однородности на множестве входных статистических данных, то внутри каждого из этих классов можно построить регрессионные зависимости вида (2) с постоянными параметрами. Полученным значениям параметров в каждом классе можно поставить в соответствие какую-либо точку из этого класса. Очевидно, что в качестве такой точки целесообразно взять среднее значение в классе. Таким образом, уравнение состояния задается в табличном виде, который затем можно аппроксимировать непрерывной зависимостью.
необходимо определить признаки, по которым можно было бы оценивать стационарность условий протекания процесса или другими словами, однородность статистических данных. Если удается выделить классы однородности на множестве входных статистических данных, то внутри каждого из этих классов можно построить регрессионные зависимости вида (2) с постоянными параметрами. Полученным значениям параметров в каждом классе можно поставить в соответствие какую-либо точку из этого класса. Очевидно, что в качестве такой точки целесообразно взять среднее значение в классе. Таким образом, уравнение состояния задается в табличном виде, который затем можно аппроксимировать непрерывной зависимостью.
В качестве таких признаков были выбраны следующие признаки – направление вектора градиента и направление и длина вектора градиента.
Рассмотрим формирование классов однородной статистики с помощью первого признака. Направление вектора ∇ ограничено соотношением:
α ∈ [0°, 360°), (4) где α - угол между вектором ∇ и вектором (0, 1). Разобьем промежутки в правой части соотношения (4)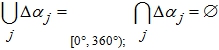 , где
, где
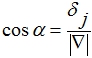 (5)
Классификация по второму признаку происходит по аналогичной схеме.
Пусть длина и направление вектора ∇ ограничены соотношениями:
(5)
Классификация по второму признаку происходит по аналогичной схеме.
Пусть длина и направление вектора ∇ ограничены соотношениями:
Разобьем промежутки в правой части соотношений (6) и (7) на несколько меньших, одинаковых промежутков ![]() ,
,
![]() .
.
Получим два множества классов длин и направлений вектора градиента: {![]() }, {
}, {![]() }. Прямое произведение этих множеств даст множество классов (
}. Прямое произведение этих множеств даст множество классов (![]() ,
,![]() ). Каждая пара значений длины вектора
). Каждая пара значений длины вектора ![]() и угла α внутри класса (
и угла α внутри класса (![]() ,
,![]() ) определяется измеренными значениями температуры в смежных узлах сетки
) определяется измеренными значениями температуры в смежных узлах сетки
![]() (8)
(8)
![]() (9)
(9)
Для экспериментальной апробации использовались статистические данные реанализа параметров атмосферы [4] за 2008 год, приведенные к среднесуточным значениям. Рассматривались процессы изменения температуры при геопотенциале 300 ГПа в узле сетки с координатами -70° северной широты; 2,5°восточной долготы.
Согласно первой предложенной методике моделирования в рассматриваемом узле было выделено 16 классов однородной статистики. В результате в узле оказалось 2 класса с непредставительным объемом выборки и далее эти классы не рассматривались. С использованием МНК было построено 14 авторегрессионных уравнений, номера которых соответствуют номерам классов, получены оценки соответствующих векторов параметров ![]() . Результаты представлены в таблице 1.
. Результаты представлены в таблице 1.
Таблица 1 - Векторы оценок параметров в соответствующем классе, полученных с помощью первой методики
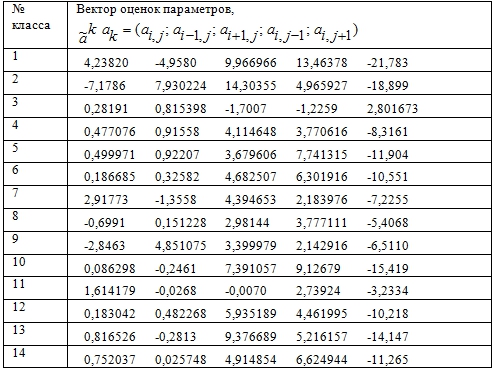
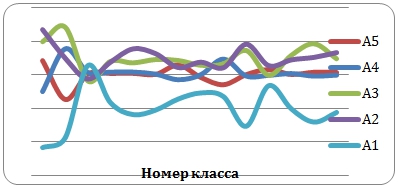
Рис.1 - Графики зависимости параметров ![]() от номера конкретного класса, полученных с помощью первой методики
от номера конкретного класса, полученных с помощью первой методики
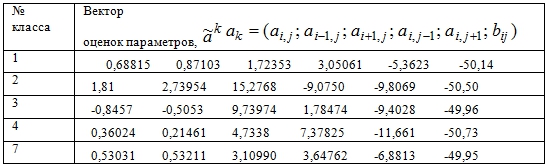
С помощью второй методики моделирования в том же узле было получено 5 классов однородной статистики. Результаты вектора оценок параметров в соответствующем классе представлены в таблице 2.
Таблица 2 - Векторы оценок параметров в соответствующем классе, полученных с помощью второй методики
На рисунке 2 представлены графики зависимости параметров от номера конкретного класса, выделенных с помощью второй методики.
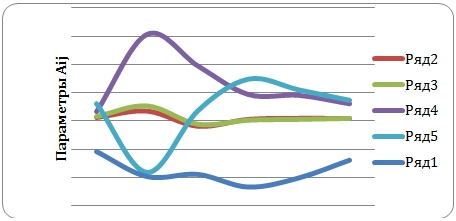
Рис.2 - Графики зависимости параметров ![]() от номера конкретного класса, полученных с помощью второй методик
от номера конкретного класса, полученных с помощью второй методик
Из рисунков 1, 2 видно, что аппроксимировать зависимости (3) непрерывно не представляется возможным, поэтому оценка зависимости осуществляется отдельно для каждого уравнения системы (2) универсальным аппроксиматорм - многослойным персептроном, с вектором входа ![]() и вектором выхода
и вектором выхода ![]() . Используемая искусственная нейронная сеть выступает как уравнение оценки состояний метеорологического процесса, а совокупность уравнений состояний и уравнение (2) как модель в пространстве метеорологических состояний. Для обучения был использован трехслойный персептрон. В качестве функций активации входного и скрытого слоя использовалась сигмоидальная функция «logsig», для выходного слоя линейная функция «purelin». Оценка эффективности работы ИНС представлена в таблице.
. Используемая искусственная нейронная сеть выступает как уравнение оценки состояний метеорологического процесса, а совокупность уравнений состояний и уравнение (2) как модель в пространстве метеорологических состояний. Для обучения был использован трехслойный персептрон. В качестве функций активации входного и скрытого слоя использовалась сигмоидальная функция «logsig», для выходного слоя линейная функция «purelin». Оценка эффективности работы ИНС представлена в таблице.
| R2 | MAPE |
| 0,875 | 2,8 % |
Литература
- Лукашин Ю.П. Адаптивные методы краткосрочного прогнозирования временных рядов / Ю.П. Лукашин // М.: Финансы и статистика. – 2003. – 416 с.
- Матвеев Л.Т. Курс общей физики атмосферы / Л.Т. Матвеев // 2-е изд. Л.: Гидрометеоиздат. – 1984. – 687 с.
- Матвеев М.Г. Модель анализа динамики векторного метеорологического процесса / М.Г. Матвеев, Михайлов В. В., Семенов М. Е., Сирота Е. А. // Вестник Воронеж. гос. ун-та. Сер. Системный анализ и информационные технологии. – 2013. – № 1. – C. 89-95.
- NCEP/DOE AMIP II Reanalysis [Электронный ресурс]. URL: http:// www. cdc. noaa.gov/cdc/data.ncep.reanalysis2.html
