OPTIMAL FORMULA FOR DETERMINING THE VOLUME OF GROWING PINE TREES UNDER CONDITIONS OF THE BAIKAL MOUNTAIN FOREST REGION

В 1981 г в Республике Бурятия издается очерк «Сосновые и лиственничные леса Бурятской АССР», составителем которого являлся С.И. Цай с соавторами

В настоящее время в оценке таксационных и морфологических показателей, как отдельных деревьев, так и насаждений в целом используются современные технологические и цифровые подходы, связанные с применением воздушных лазерных лидаров, наземных лазерных лидаров, нелинейных моделей при построении образующих стволов, нейронных сетей, оценка временных изменений

Несмотря на достаточно большое число научных исследований, посвященных проблеме изучения и определения формы, объемов стволов различных пород, вопрос об особенностях формирования и влияния различных факторов на объемообразующие признаки остается открытым.

Сосна обыкновенная (Pinus sylvestris L.), имея широкий ареал произрастания, и способность расти в различных лесорастительных условиях, характеризуется многообразием формы и объёмов стволов.

Сосна, являясь одной из основных целевых хвойных пород и постоянным объектом эксплуатации, формирует нестабильную среду произрастания. По этой причине необходима идентификация особенностей ростовых процессов в определенных лесорастительных условиях, с целью уточнения особенностей объемных параметров древостоев и дальнейшей детализации объемных, сортиментных таблиц.

Цель исследования – определить оптимальную универсальную формулу для оценки объёма растущих деревьев сосны в условиях Байкальского горного лесного района.

Исследования проводилось по результатам камеральной обработки лесных участков в условиях Верхне-Березовского участкового лесничества Улан-Удэнского лесничества. В соответствии с целью поставлены следующие программные задачи: выполнить измерительные работы учетных деревьев на лесных участках; представить таксационную характеристику лесных участков; установить соотношение высот и диаметров путем определения разряда высот; выполнить расчеты объемов растущих деревьев следующими способами: основная формула, уравнения Третьякова Н.В., Ли-Чан-Гена, Денцина, Дементьева Н.Н., Цая С.И. c соавторами; выявить оптимальную формулу для определения объема растущих деревьев.

Пробные площади подбиралась с учетом разных таксационных показателей и условий произрастания насаждений. Перечет производился способом сплошного перечета. Значительное внимание уделялось таким показателям как составу насаждения, типу леса и экспозиции склона.

Для определения объемов деревьев в первую очередь необходимо установить разряд высоты и выявить соотношение диаметров и высоты деревьев на каждом участке. Для этого построены графики функций зависимости высоты и диаметра по каждому участку у деревьев по ступеням толщины в 3-х повторностях. Диаграммы соотношения высоты и диаметра выровнены параболическими уравнениями (таблица 1). Коэффициент детерминации указывает на достаточно высокую адекватность моделей. Минимальный коэффициент детерминации –  0,76 максимальный – 0,99.

С учётом близости линий и для минимизации ошибок использовалась средняя высота для каждой ступени толщины. Для дальнейшего установления разряда высот применялась местная объемная таблица, составленная применительно к сосновым насаждениям Бурятии

Для решения поставленной цели выполнен расчёт объёмов растущих деревьев по ряду эмпирических формул

Стандартная формула.

Изучая связь видовых чисел и коэффициентов формы, М.Е. Ткаченко пришел к выводу, что независимо от древесной породы, при любых естественно-исторических условиях, равной высоте и коэффициенте формы q2 деревья имеют близкие значения видовых чисел. Данная закономерность позволила построить таблицу всеобщих видовых чисел.

(1)

где, d – диаметр на высоте 1,3 м, см;

 Нcp – средняя высота, м;

 ƒ – видовое число.

Объем деревьев по каждому участку варьировал следующим образом. Участок №1 в пределах от 0,279 до 2,488 м3; участок № 2 от 0,178 до 1,422 м3; участок №3 от 0,033 до 1,372 м3; участок № 4 от 0,065 до 1,510 м3.

Формула Третьякова Н.В.

Ствол растущего дерева является качественно иным объектом таксации по сравнению с объемом срубленного дерева. Исходя из этого, вычислялся объем отдельных деревьев по формуле (2).

(2)

Данные показывают, что объем на всех четырех участках варьировал от 0,032 до 2,226 м3. 

Формула Ли-Чан-Ген.

Чтобы найти объем растущего дерева на каждом участке и каждой ступени толщины использовалась формула (3):

(3)

где, Fэ – эмпирическое видовое число (0,40)

Данные указывают на значительную изменчивость объемов в пределах от 0,032 до 2,237 м3.

Формула Денцина.

Немецкий лесовод Денцин вывел упрощенную формулу для приближенного определения объема ствола:

(4)

Данные таблицы 4 указывают на имеющуюся вариацию объемов 0,064 - 2,704 м3.

Формула Дементьева Н.Н.

Способ Н. Н. Дементьева основан на том, что при среднем коэффициенте формы 0,65 видовое число принято равным 0,425. Если коэффициент формы больше среднего, тогда поправка вводится со знаком плюс, и наоборот. В этом случае формула имеет следующий вид:

(5)

где, К – поправочный коэффициент, (+3).

Так, для стволов, у которых q2=0,7, поправка +3 м; при q2=0,75 поправка +6 м, при q2=0,6 поправка со знаком минус, т.е. -3 м.

Согласно расчётам, вариация объема 0,034 - 2,374 м3.

Уравнение Цая С.И.

Для определения объема древесных стволов по разрядам высот Цаем С.И. предложены следующие формулы:

(6)

(для 5 разряда высот),

(7)

(для 6 разряда высот),

В таблице 2 приведены объемы отдельных деревьев согласно уравнениям 6,7.

Данные таблицы показывают, что в зависимости от разряда высот объем варьирует в пределах от 0,035 м3 до 2,200 м3.

Наиболее адекватным местным условиям произрастания сосны являлись уравнения С.И. Цая, представленные в соответствии с разрядом высоты. Данные расхождений объемов по каждому лесному участку в процентах приведены в таблице 3.

На всех лесных участках наблюдалась общая трендовая закономерность на увеличение величины погрешности с ростом размера ступени толщины (таблица 3, рисунок 1). При этом самая значительная погрешность в тонкомерной части и после 28 см. В среднемерных ступенях выявлена минимальная погрешность – 20-28 см. Диаграмма (на примере лесного участка №3) демонстрирует особенности динамики величины ошибок в сравнении с формулой Цая С.И (рисунок 1).

С учётом данных всех участков можно констатировать, что оптимальной формулой для расчёта объёма отдельных деревьев является формула Ли-Чан-Гена. Близка по значениям также формула Денцина.

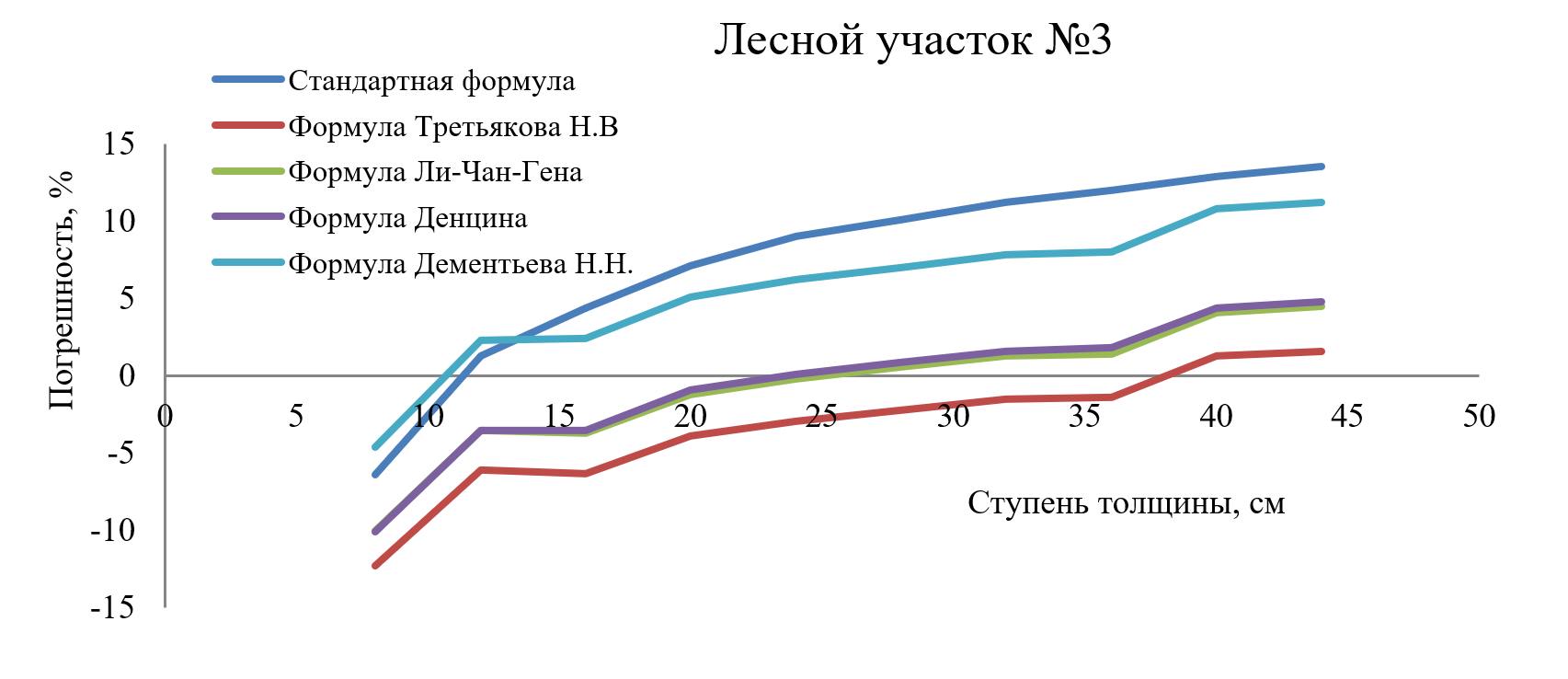
Рисунок 1 - Динамика трендовых линий погрешностей объёма по различным формулам с учётом ступеней толщины (на примере лесного участка №3)

DOI:10.23670/IRJ.2024.139.94.4

В результате выполненных работ получены следующие итоги.

- Замеры диаметров и высот растущих деревьев показали, что для условий Улан-Удэнского лесничества соотношение показателей соответствует V и VI разряду высот.

- Объёмы растущих деревьев определялись по стандартной формуле, уравнениям Н.В. Третьякова, Ли-Чан-Гена, Денцина, и Н.Н. Дементьева.

- Сравнение объёмов выполнялось с местной формулой, полученной для районов Бурятии под руководством С.И. Цая.

- Максимальная положительная погрешность составила +13,5%, а минимальная -12,3%. Самые значительные различия характерны для тонкомерных и крупномерных ступеней толщины.

- Результаты расчётов объёмов показали, что с учётом разнообразия условий произрастания растущих деревьев для исходного района оптимальной, помимо формулы С.И. Цая является формула Ли-Чан-Гена, близка по точности к этой оценке уравнение Денцина, далее Н.В. Третьякова, Н.Н. Дементьева и стандартная формула.

Оптимизация способов определения объёмов растущих деревьев позволяет решать комплекс как хозяйственных, так и эколого-оценочных задач важных для рационального лесопользования.