AN EXPERIMENT AND CALCULATIVE EVALUATION OF DEFORMATION CHARACTERISTICS OF A SPECIAL LABORATORY SPECIMEN FOR MECHANICAL TESTS

Zenkov E. V.

doi:10.23670/IRJ.2024.139.169

AN EXPERIMENT AND CALCULATIVE EVALUATION OF DEFORMATION CHARACTERISTICS OF A SPECIAL LABORATORY SPECIMEN FOR MECHANICAL TESTS

Research article

DOI:

https://doi.org/10.23670/IRJ.2024.139.169

Issue: № 1 (139), 2024

Suggested:

22.11.2023

Accepted:

15.01.2024

Published:

24.01.2024

217

8

XML

PDF

Abstract

The article describes experimental studies of the stress-strain state (SSS) characteristics of a laboratory prismatic specimen used to evaluate the structural strength of a material. This specimen allows to model in its working zone biaxial tension of material with different ratio of values of principal stresses, and at the same time its loading is carried out on standard testing equipment with one power drive. The displacements and deformations of the specimens are studied at the stage of their elastic deformation on the basis of the digital image correlation method. Quantitative analysis of comparison of the results obtained by MCIA with the results of physical experiment modelling based on the finite element method is performed. According to the totality of the presented data, the obtained experimental and calculated displacements and deformations have a discrepancy not exceeding 14%.

Keywords:

stress-strain state, prismatic specimen, finite element method, digital image correlation method.

1. Введение

Исследования прочности деталей машин и конструкций в зависимости от вида возникающего в них напряженно-деформированного состояния (НДС) проводятся, как правило, на основе испытания специальных лабораторных образцов, способных создавать в своей рабочей зоне НДС с требуемыми параметрами

, , . В свою очередь, наибольшую трудоемкость на лабораторных образцах вызывает моделирование НДС, характеризуемое различным соотношением величин главных напряжений и их знаков .

В работе описываются экспериментально-расчетные исследования НДС (далее – деформационных характеристик) лабораторного призматического образца, способного моделировать в своей рабочей зоне двухосное растяжение материала с различным соотношением величин главных напряжений с целью оценки достоверности этого НДС, полученного в результате расчетных исследований методом конечных элементов (МКЭ). Испытание такого образца осуществляется на стандартном оборудовании с одним силовым приводом

. Как показали результаты этих исследований , варьирование геометрических параметров указанного образца позволяет воспроизводить требуемое двухосное НДС, аналогичного тому НДС, которое возникает в исследуемой конструкции, прочность которой оценивается.

2. Методы и принципы исследования

Для оценки достоверности деформационных характеристик предложенных образцов, полученных в результате исследований по МКЭ, проводились экспериментальные исследования перемещений и деформаций этих образцов. В исследовании использовался метод корреляции цифровых изображений (МКЦИ)

, реализованный в цифровой оптической системе Vic-3D , . Данная система представлена на рис. 1. Суть метода МКЦИ сводится к отслеживанию смещений одних и тех же физических точек на поверхности тела до и после его деформирования. Свидетелями этому являются смещения элементов системы хаотически распределенных по поверхности объекта и неразрывно связанных с ним малоразмерных меток-пятен – спекл-структуры . Для анализа полей перемещений и деформаций необходимы, как минимум, два изображения поверхности испытуемого объекта со спекл-структурой. Одно из этих изображений, как правило, регистрируется в исходном состоянии объекта, а второе – при заданной нагрузке. В ходе обработки полученных изображений вся поверхность объекта разбивается на фрагменты и анализируется перемещение спекл-структуры в пределах каждого элементарного окна , .

Наиболее важным параметром, определяющим точность получаемых экспериментальных данных на основе использования системы Vic–3D, является уровень дискретности спекл-структуры, связанной с поверхностью объекта. Для обеспечения метрологически необходимой спекл-структуры на поверхности образца и оценки достоверности получаемых деформационных характеристик проведены тестовые испытания на растяжение плоских образцов, имеющих центральные круглые отверстия

, . В соответствии с измерительная погрешность МКЦИ при определении всех компонент деформаций около центрального отверстия не превысила 8%.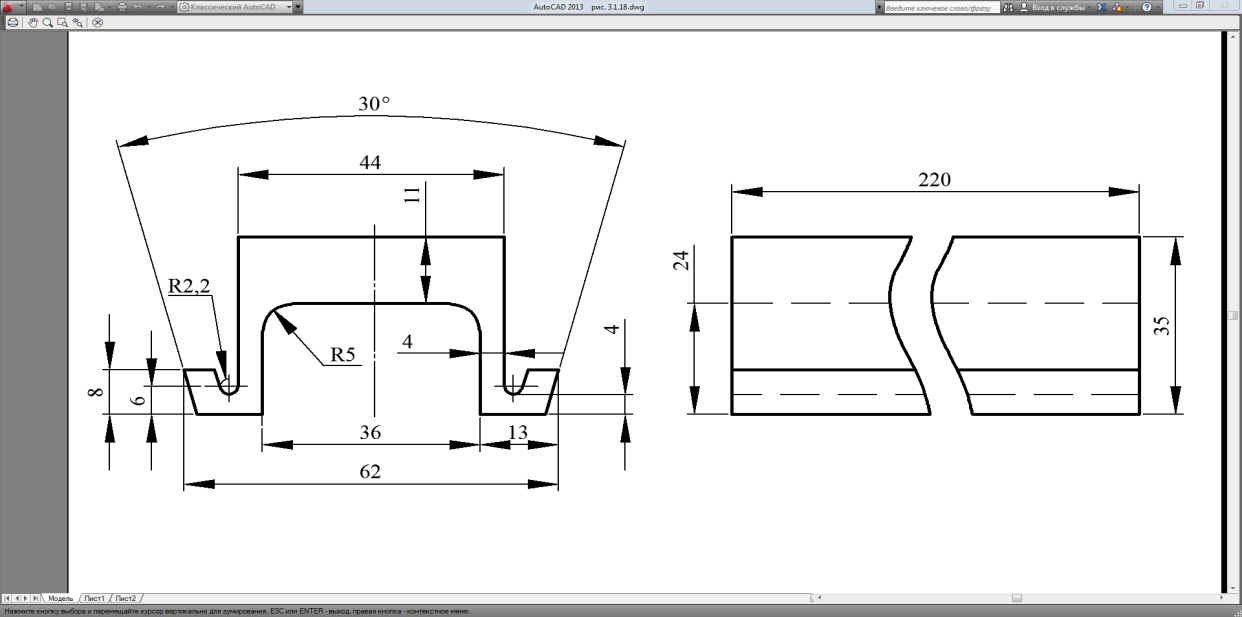

Для оценки деформационных характеристик призматических образцов в процессе их испытания использовался образец с геометрическими размерами, представленными на рис. 2.

Рисунок 1 - Геометрические размеры призматического образца

Образцы были изготовлены из полосового сортового проката методом фрезерования. Нагружение, соответствующее упругому деформированию образцов, осуществлялось на испытательной машине Instron 5989 (рис. 3). Для создания двухосного растяжения материала в образце использовались опоры 3 и 4 (рис. 3, а), последняя размещаемая на столе испытательной машины (рис. 3, б).

Измерение перемещений и деформаций выполнялось для боковой поверхности призматического образца, доступной для фотофиксации цифровыми камерами с помощью МКЦИ. Нагружение призматического образца выполнялось при постоянной скорости нагружения 2 мм/мин. Таким образом, полученные экспериментальные поля компонент перемещений и деформаций позволят далее сравнить их с результатами соответствующих расчетными данными по МКЭ

.

На рис. 4,а представлено начальное состояние исследуемого образца в опорах, установленных на стол испытательной машины Instron 5989, а на рис. 4,б – конечное состояние образца, деформированное упруго усилием испытательной машины.

Рисунок 2 - Лабораторная установка для испытания призматических образцов

Примечание: а – базирование образца в опорах (1 – образец, 2 – усилие, создаваемое толкателем испытательной машины, 3 – концевые опоры, 4 – призматическая опора), б – базирование призматической опоры с образцом на рабочем столе испытательной машины

Рисунок 3 - Деформированное состояние призматического образца

Примечание: а – начальное состояние, б – конечное состояние

Определение характеристик перемещений и деформаций осуществлялось на стадии упругого деформирования материала образца. Эта стадия определялась по виду диаграммы нагружения образца испытательным усилием, значение величины которого соответствовало линейному участку этой диаграммы. Найденное усилие далее использовалось в качестве исходных данных для численного моделирования характеристик перемещений и деформаций призматического образца по МКЭ.

3. Результаты экспериментальных и расчетных исследований

На рис. 4-6 представлены результаты распределения полей перемещений и деформаций боковой поверхности исследуемого образца на стадии упругого деформирования его материала, зарегистрированное с помощью системы Vic–3D. На рис. 4, а показано цифровое отображение распределения полей продольных Δlxx перемещений, на рис. 4, б – осевых Δlyy перемещений спекл-структуры материала образца. На рис. 5, в приведено цифровое поле продольных εxx деформаций, на рис. 5, г – осевых εyy деформаций спекл-структуры перемещений реперных точек материала. На рис. 6, д представлены цифровые поля распределения сдвиговой εxy деформации, на рис. 6, е – интенсивности εi деформаций.

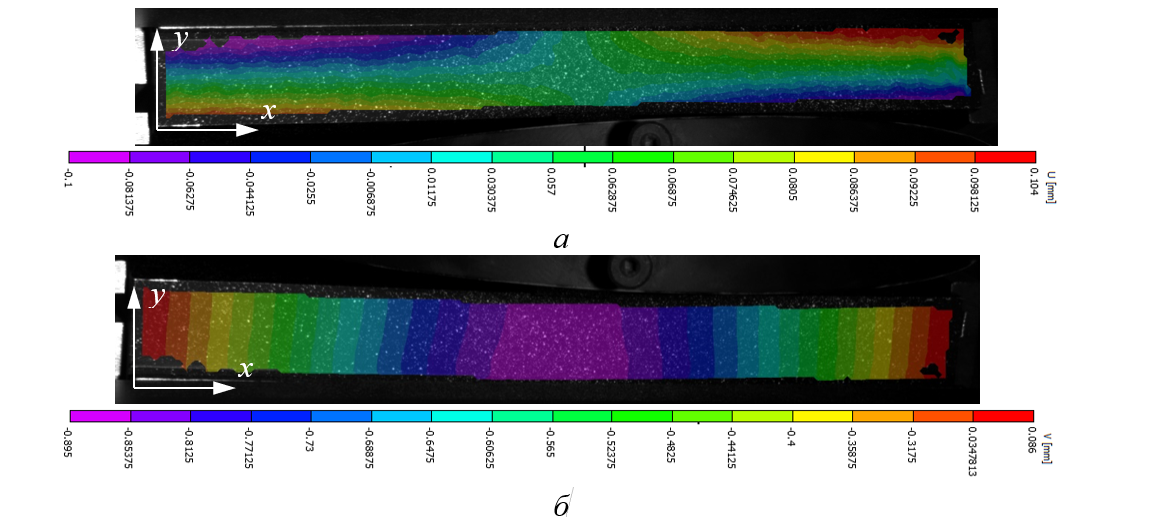
Рисунок 4 - Распределение экспериментального поля продольных Δlxx (а) и осевых Δlyy(б) перемещений

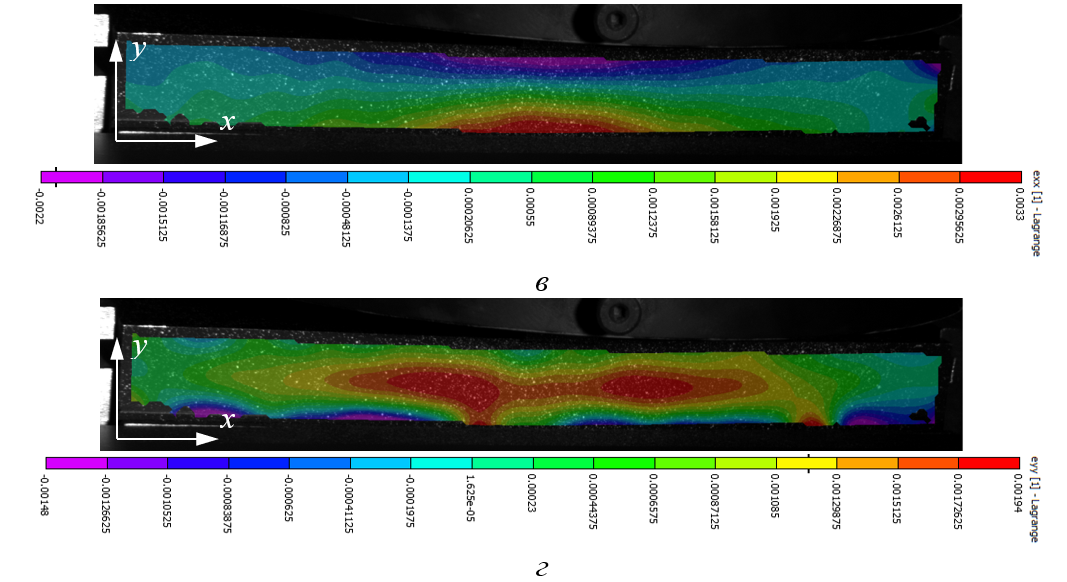
Рисунок 5 - Распределение экспериментального поля продольных εxx (в) и осевых εyy (г) деформаций

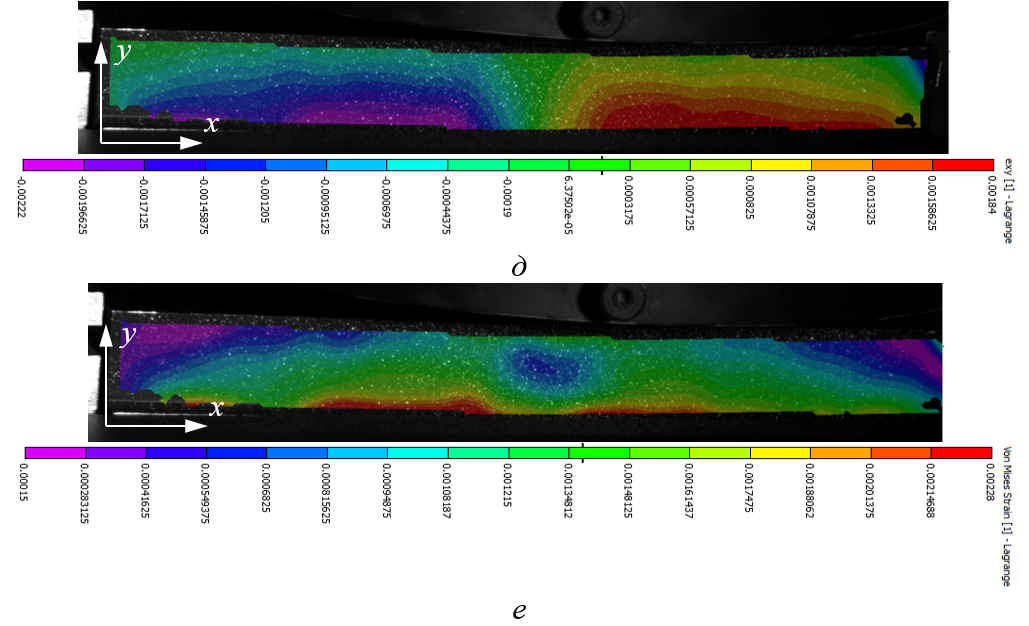
Распределение экспериментального поля сдвиговой εxy (д) деформации и интенсивности εi (е) деформаций в результате обработки системой Vic-3D

Рисунок 6 - Распределение экспериментального поля сдвиговой εxy (д) деформации и интенсивности εi (е) деформаций в результате обработки системой Vic-3D

На рис. 7-9 представлены расчетные значения перемещений и деформаций узлов КЭ-модели призматического образца по результатам упругого деформирования, выполненные в системе Femap with NXNastran по МКЭ . При этом значение усилия в вычислительном эксперименте соответствовало значению на динамометре испытательной машины в момент фиксации экспериментальных данных, приведенных на рис. 4-6.

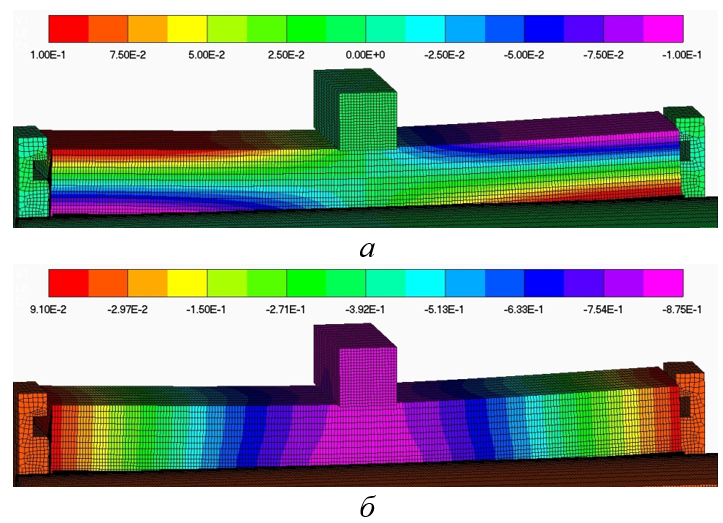
Рисунок 7 - Распределение расчетного поля продольных Δlxx (а) и осевых Δlyy(б) перемещений

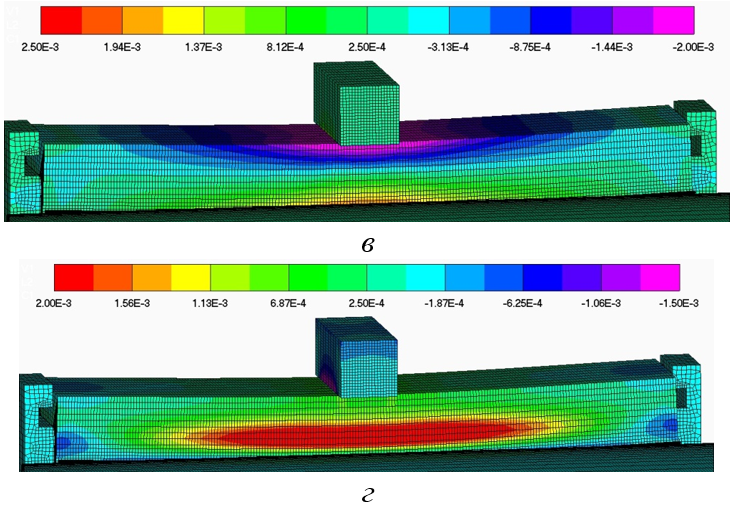
Рисунок 8 - Распределение расчетного поля продольных εxx (в) и осевых εyy (г) деформаций

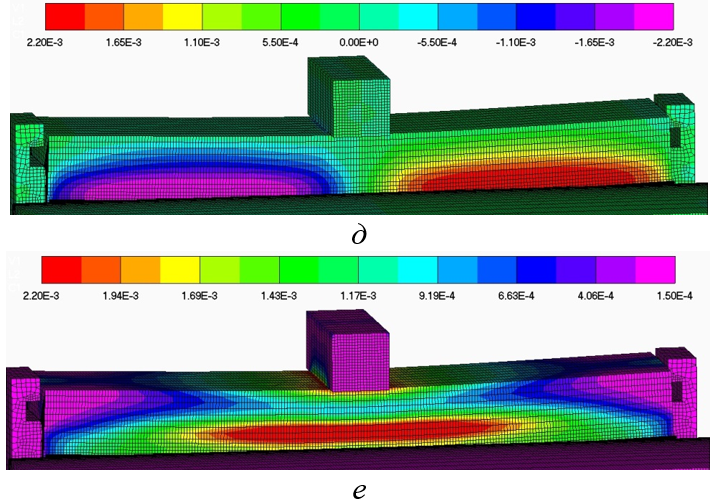
Распределение расчетного поля сдвиговой εxy (д) деформации и интенсивности εi (е) деформаций в результате вычислительного эксперимента по МКЭ

Рисунок 9 - Распределение расчетного поля сдвиговой εxy (д) деформации и интенсивности εi (е) деформаций в результате вычислительного эксперимента по МКЭ

Анализ сравнения результатов съемки спекл-структуры боковой поверхности образца по МКЦИ (рис. 4-6) с соответствующими данными расчётного исследования (рис. 7-9) в условиях упругого деформирования материала по представленным компонентам перемещений и деформаций показывает их качественное сходство. Эти результаты также позволяют заключить, что разработанные расчетные модели деформирования призматических образцов, моделирующих в своей рабочей зоне двухосное растяжение материала, а также проведенные на их основе вариантные вычислительные исследования, с достаточной степенью точности отражают свойства физического прототипа. В свою очередь, адекватность численных моделей подтверждена количественно сопоставлением деформационных характеристик при численном и физическом экспериментах в контрольных точках исследуемой поверхности образца, расположенных на ней в определенном порядке, представленным на рис. 10.

В качестве меры относительной погрешности расхождения результатов физического эксперимента при использовании системы Vic-3D с данными численного моделирования рассматривалось отношение

где χмкэ – расчётное значение деформационных характеристик по МКЭ, χмкци – соответствующее экспериментальное значение по МКЦИ.

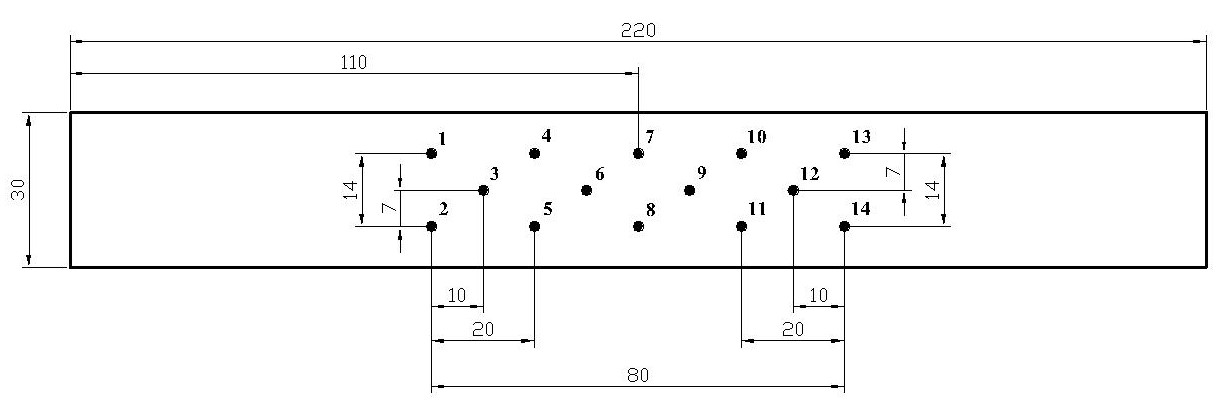
Рисунок 10 - Расположение контрольных точек на боковой поверхности образца

На рис. 11 представлены значения погрешности расхождения ε компонент перемещений и деформаций во всех 14 контрольных точках исследуемой поверхности (см. рис. 10).

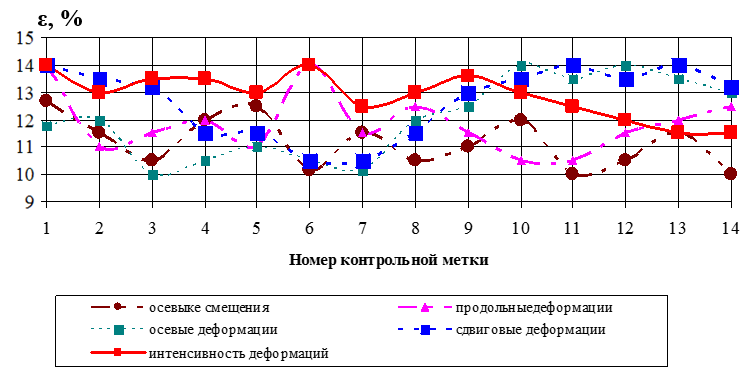
Рисунок 11 - Погрешность расхождения сравниваемых перемещений и деформаций в контрольных точках исследуемой поверхности образца

Результаты, представленные на рис. 11, в совокупности показывают, что компоненты перемещений и деформаций исследуемой поверхности образца, полученные по МКЭ (рис. 7-9) и по МКЦИ (рис. 4-6), имеют расхождение в диапазоне 10-14%.

4. Заключение

По совокупности представленных экспериментальных данных можно заключить, что численная модель деформирования образцов призматического типа позволяет определять их НДС с относительной погрешностью, не превышающей 14%. Это обстоятельство подтверждает адекватность принятых расчетных схем и дискретных моделей, разработанных на основе трехмерных уравнений теории упругости.

Полученный в работе анализ деформационных характеристик призматических образцов позволяет в дальнейшем использовать эти образцы для оценки конструкционной прочности различных материалов и реализовать предложенную в

расчётно-экспериментальную методику расчёта деталей машин и конструкций на статическую прочность с целью уточнения прочностных параметров материала.

Additional materials

Not specified

Financing

Авторы не получали финансовой поддержки для проведения исследования, написания и публикации статьи

Acknowledgements

Not specified

Conflicts of interests

Not specified

References

Kogaev V.P. Raschety detaley mashin i konstruktsiy na prochnost' i dolgovechnost': Spravochnik [Calculations of Machine Parts and Structures for Strength and Durability: handbook] / V.P. Kogaev, N.A. Makhutov [et al.]. — M.: Mashinostroenie, 1985. — 224 p. [in Russian]
Birger I.A. Raschot na prochnost' detaley mashin [Strength Calculation of Machine Parts] / I.A. Birger, B.F. Shorr and [et al.]. — M.: Mechanical Engineering, 1993. — 640 p. [in Russian]
Gagarin Yu.A. Issledovaniye povedeniya defektov v polyakh rastyagivayushchikh i szhimayushchikh napryazheniy [Study of the Behavior of Defects in Fields of Tensile and Compressive Stresses] / Yu.A. Gagarin, S.N. Pichkov // Problemy prochnosti i plastichnosti. Mezhvuzovskiy sbornik [Problems of Strength and Plasticity. Interuniversity collection]. — Nizhny Novgorod: UNN Publishing House, 2000. — P. 11-116. [in Russian]
Vansovich K.A. Ustalostnyye ispytaniya stal'nykh krestoobraznykh obraztsov s poverkhnostnoy treshchinoy pri dvukhosnom nagruzhenii [Fatigue Testing of Steel Cross-shaped Specimens with a Surface Crack under Biaxial Loading] / K.A. Vansovich, V.I. Yadrov // Omskiy nauchnyy vestnik [Omsk Scientific Bulletin]. — 2012.— No. 3 (113). — p. 117-121. [in Russian]
Zenkov E.V. Povysheniye dostovernosti raschetov detaley mashin s kontsentratorami napryazheniy pri dvukhosnom rastyazhenii: dissertatsiya na soiskaniye uchenoy stepeni kand. tekhn. nauk [Increasing the Reliability of Calculations of Machine Parts with Stress Concentrators under Biaxial Tension: dissertation for the scientific degree of Ph.D. in Tech. Sciences] / E.V. Zenkov. — Irkutsk: IRNITU, 2015. — 192 p. [in Russian]
Zenkov E.V. Deformation of Prismatic Samples of U-shaped Grooves and Their Stress-strain State / E.V Zenkov., D.A. Elovenko // Lecture Notes in Mechanical Engineering. — 2020. — p. 337-348.
Wildeman V.E. Eksperimental'nyye issledovaniya svoystv materialov pri slozhnykh termomekhanicheskikh vozdeystviyakh [Experimental Studies of the Properties of Materials under Complex Thermomechanical Influences] / V.E. Wildeman, M.P. Tretyakov and [et al.]. — M.: FIZMATLIT. 2012. — 204 p. [in Russian]
Odintsev I.N. Primeneniye optiko-korrelyatsionnykh metodov v zadachakh eksperimental'noy mekhaniki [Application of Optical-correlation Methods in Problems of Experimental Mechanics] / I.N. Odintsev, A.A. Apalkov and [et al.]. // Progressivnyye tekhnologii i sistemy mashinostroyeniya [Progressive Technologies and Mechanical Engineering Systems]. — 2015. — No. 1 (51). — p. 152-160. [in Russian]
Sutton M.A. Image Correlation for Shape, Motion and Deformation Measurements / M.A. Sutton, J.-J. Orteu and [et al.]. — University of South Carolina, Columbia, SC, USA, 2009. — 364 p.
Zenkov E.V. Metodika eksperimental'nogo issledovaniya poley deformatsiy na osnove ispol'zovaniya tsifrovoy opticheskoy sistemy [Methodology for Experimental Research of Deformation Fields Based on the Use of a Digital Optical System] / E.V. Zenkov, A.A. Andreeva // Problemy transporta Vostochnoy Sibiri. Sbornik nauchnykh trudov IV Vserossiyskoy nauchno-prakticheskoy konferentsii IrGUPS [Problems of Transport in Eastern Siberia. Collection of scientific papers of the IV All-Russian Scientific and Practical Conference of IrSUPS]. — Irkutsk, IrGUPS, 2013. — Part 1. — p. 95-99. [in Russian]
Shimkovich D.G. Femap & Nastran Inzhenernyy analiz metodom konechnykh elementov [Femap & Nastran. Engineering Analysis by Finite Element Method] / D.G. Shimkovich. — M.: DMK Press, 2008. — 704 p. [in Russian]
Zenkov E.V. A Comparative Analysis of the Stress-strain State of Disc Specimens in Assessing the Structural Strength of Materials / E.V. Zenkov, L.B. Tsvik // Engineering Solid Mechanics. — 2022. — No. 1. — p. 25-34. — DOI: 10.5267/j.esm.2021.12.001

Review

All articles are peer-reviewed. But the reviewer or the author of the article chose not to publish a review of this article in the public domain. The review can be provided to the competent authorities upon request.

Author information

Affiliation:Irkutsk National Research Technical University, Irkutsk, Russian Federation

Role:Author, Methodology, Management, Writing, reviewing and editing, Research data analysis, Analysis

ORCID:0000-0003-4414-0307

ELIBRARY AUTHOR ID:676168

RESEARCHER ID:E-4990-2017

Article metrics

Downloads:8

ViewsDownloads

Views

Total: