A CALCULATION OF OPTIMAL TEMPERATURE AND DIMENSIONAL PARAMETERS OF A LIQUID CHLORINE VAPORIZER CATCHER
A CALCULATION OF OPTIMAL TEMPERATURE AND DIMENSIONAL PARAMETERS OF A LIQUID CHLORINE VAPORIZER CATCHER
Abstract
In accordance with regulatory documents, modern vacuum chlorinators are one of the main units in the technology of chlorine consumption for disinfection of drinking and recycled water at waste water treatment facilities. The requirements established by the "Safety rules for chlorine and chlorine-containing media industry" approved by the Order of the Federal Service for Environmental, Technological and Nuclear Supervision from 20.11.2013 № 554 and other regulations ensure the safe operation of equipment installed at hazardous facilities. One of the conditions for accident-free operation of vacuum chlorinators is to prevent liquid chlorine fraction from getting into its components. For this purpose, the "liquid chlorine vaporizer" device has been developed. Calculation, laboratory and production tests of optimal temperature and size ratios of the "vaporizer catcher" chamber were performed.
1. Введение
Хлораторы непрерывного действия в основном являются стационарными аппаратами. Наиболее эффективными из них являются вакуумные хлораторы, в которых дозируемый газ находится под разрежением. Это предотвращает проникновение газа в помещение, что возможно при использовании напорных хлораторов.
Поскольку используемый хлор является опасным токсическим газом, его перевозка, хранение и использование регламентируются «Правилами безопасности производства хлора и хлорсодержащих сред», утвержденными приказом Федеральной службы по экологическому, технологическому и атомному надзору от 20.11.2013 № 554 , которые приняты в 2013 году и учитывают и включают в себя мировой опыт эксплуатации хлора. В частности, правилами предусмотрено, что хлораторы должны содержать узлы обеспечивающие непрерывное поддержание заданной величины разрежения газа (вакуума) на входе дозатора при изменении в широких пределах следующих характеристик: давления хлора в резервуаре, нормы расхода газа, уровня разрежения, создаваемого эжектором, защиту от проникновения в хлоропроводы и узлы хлоратора воды из эжектора, автоматическое прекращение подачи хлора хлоратором при прекращении подачи питающей воды в эжектор , , , . Так как в хлоратор должен подаваться только газообразный хлор, во избежание проскока жидкой фракции или замерзания хлора, подача хлора из одного баллона без подогрева не должна превышать 0,5—0,7 кг/ч. В противном случае для исключения аварий используются устройства, в которых происходит испарение жидкой фракции хлора.
2. Основная часть
Качество работы хлораторов зависит от схемы подключения хлоратора и условий съема газообразной фракции хлора с баллонов, контейнеров или других емкостей, содержащих жидкий хлор, так как проскок капель жидкого хлора, образовавшегося в хлоропроводах, может также происходить вследствие перепада температур, временного отключения подачи хлора и т.п. (рис. 1), что может привести к нарушению работы хлораторов.
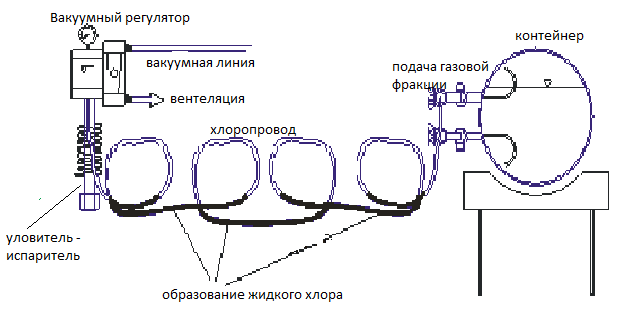
Рисунок 1 - Образование жидкого хлора в соединительных хлоропроводах

Рисунок 2 - Уловитель-испаритель жидкого хлора М100С
В случае стационарного испарения диффузионный поток пара вещества капли через концентрическую с каплей сферическую поверхность с радиусом d есть величина постоянная, выражаемая уравнением
где D – коэффициент диффузии пара, ρ - его плотность (г⋅см-3).
Интегрирование уравнения (1) дает
Если обозначить через ρ∞ плотность пара на бесконечно большом расстоянии от капли, то имеем следующие граничные условия:
и, согласно упомянутому выше предположению,
где r – радиус капли.
Из условий (3) следует:
Подстановка условия (1 - 4) приводит к формуле Максвелла:
Таким образом, скорость испарения капель при соблюдении условия (4) полностью определяется скоростью диффузии пара в окружающей среде, т. е. мы имеем здесь только диффузионный режим испарения. Из формулы (6) следует, что в рассматриваемом случае скорость испарения капель в газообразной сфере пропорциональна не поверхности капли, как при испарении в вакууме (т. е. при кинетическом режиме испарения), а радиусу капли.
Если принять, что пар вещества подчиняется законам идеальных газов, и выразить концентрацию через парциальное давление пара p:
то формула Максвелла примет вид
,
где М – молекулярный вес испаряющегося вещества в газообразном состоянии. При этом, если выражать давление в мм рт. ст., а плотность в г/см3, для газовой постоянной надо взять значение R=82,05⋅760=62 360 (см3⋅мм рт. ст.⋅град-1⋅моль-1).
Строго говоря, испарение капель не может быть стационарным процессом, так как радиус капель, а, следовательно, и скорость испарения непрерывно уменьшаются. Однако при соблюдении условия ρ0<<ρк (ρк –плотность капли) можно считать испарение квазистационарным, т. е. принять, что скорость испарения в каждый данный момент выражается формулой (6). Так как по смыслу величины
где t – время, а m=4/3πr2ρк – масса капли, формулу (6) можно представить в виде
или в виде
,
Где S=4πr2ρк — поверхность капли.
Интегрирование этих уравнений дает
где r0 и S0 — радиус и поверхность капли в начальный момент. Таким образом, поверхность капли есть линейная функция времени.
За t0 время капля полностью испаряется, т.е. r становится равным 0
В соответствии с теорией молекулярной физики [10], зависимость давления насыщенного газа от температуры можно выразить по формуле:
где p – давление насыщенного пара, зависимость которого от температуры приведена в таблице 1.
Таблица 1 - Зависимость давления насыщенного газа от температуры
Т, К | 189 | 216,3 | 260,7 | 283 | 316,3 | 349,6 | 394,1 |
Р0, кП | 3,479 | 32,24 | 233,2 | 484,9 | 1180,6 | 2419,0 | 5273,1 |
Для нахождения и из таблицы выберем 3 значения, поставим их в (4.11) и решим систему линейных уравнений от 3-х переменных A, B и C.
A=21,9465; B=2718,1220; C=1,0908.
Тогда формула (11) примет вид
Рассчитаем минимальную температуру необходимую для испарения капли хлора. Для того чтобы капля испарилась необходимо, чтобы давление газа (хлора) в трубе (грязевике) было меньше чем давление насыщенного газа поверхности капли, т.е. p0≥p. В процессе эксплуатации оборудования давление газа в системе находится в диапазоне 0,5÷5 атм. или 50,66÷506,63 кПа.
Тогда получаем неравенство или,
численное решение, которого дает необходимое значение для температуры.
Таким образом, T≥284,47 или t≥11,47C0, т. е при определенном значении температуры и давлении 5 атм. начинается процесс испарения хлора.
Оптимальная температура для работы испарителя рассчитывается из предположения, что капля за время падения ее в грязевике должна испарится. Пусть капля в испарителе свободно падает с ускорением g, тогда время падения капля определяется
где H высота трубы испарителя (грязевика)
Пусть H=15 см, g=9,8(м/с2).
Поставляя данные в (13) получаем tn=0,175 c.
В реальности капля падает не свободно, на нее действует сила сопротивления хлорного газа и архимедова сила. Поэтому время падения капли больше чем вычисленное значение.
Из введенного критерия оптимальной работы уловителя-испарителя, что капля хлора полностью испаряется, не опустившись до дна трубы испарителя, следует,
Это уравнение можно решить любым численным или графическим методом. В качестве примера введем следующие данные
r0=0,5⋅10-3 м (параметр для каждой задачи нужно уточнять),
ρк=1,4⋅103 кг/м3
D=0,033м2/час (параметр уточнить)
ρ∞=5 атм=506б625 кПа
R=82,05⋅101,325=8313,715⋅10-6(м3⋅кПа⋅град-1⋅моль-1)
M=71(г/моль)=71⋅10-3(кг/моль)
Поставляя данные в (14) получаем время полного испарения капли жидкого хлора.
T здесь абсолютная температура (273+градус по Цельсию).
На рис. 4. представлен полученный график зависимости времени полного испарения капли жидкого хлора от температуры трубы.
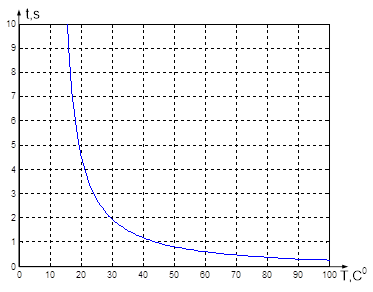
Рисунок 3 - График зависимости времени полного испарения капли жидкого хлора от температуры трубы
3. Заключение
Произведенный расчет позволяет обоснованность выбора параметров (габаритных размеров, мощность нагревательного элемента, материалы грязевика уловителя-испарителя). Полученные технические характеристики для корректной работы уловителя-испарителя жидкого хлора представлены в таблице 2. Созданная по полученным данным опытная модель (см. рис.2) подтвердила расчётные результаты и была внедрена в производство.
Таблица 2 - Технические характеристики уловителя-иcпарителя жидкого хлора М100С
Параметр | Ед. изм. | Значение |
Напряжение термоэлектрического нагревателя | В | 24 |
Потребляемая мощность нагревателя | Вт/м | 25 |
Температура нагревателя | 0С, не более | 85 |
Масса | кг, не более | 5,5 |
Габаритные размеры | м | 0,51 х 0,12 |
